Линейная функция – одна из основных математических моделей, широко применяемых в науке и практических задачах. Ее график представляет собой прямую линию на координатной плоскости. Одним из важных параметров линейной функции является коэффициент наклона, который отражает ее наклон относительно оси X.
Коэффициент наклона определяется как отношение изменения значений функции к соответствующему изменению аргумента. Он показывает, насколько быстро функция меняется по отношению к изменению аргумента. Геометрический смысл коэффициента наклона заключается в том, что он представляет собой тангенс угла наклона прямой линии.
Рассчитать коэффициент наклона линейной функции можно по формуле: m = (y2 - y1) / (x2 - x1), где (x1, y1) и (x2, y2) – координаты двух точек на прямой. Эта формула основана на принципе изменения отношения приращений значений функции и аргумента.
Знание коэффициента наклона линейной функции позволяет проводить различные анализы и прогнозы. Он может использоваться для определения скорости изменения физических величин, расчета градиента уровня в географии, определения темпов роста или убывания финансовых показателей и многих других прикладных задачах.
Что такое линейная функция

Чтобы рассчитать коэффициент наклона линейной функции, необходимо знать две точки на графике функции. После этого можно воспользоваться формулой:
k = (y2 - y1) / (x2 - x1),
где (x1, y1) и (x2, y2) – координаты выбранных точек.
Линейные функции широко используются в различных областях, таких как физика, экономика, инженерия и т.д. Они позволяют моделировать и анализировать различные процессы и явления в реальном мире. Коэффициент наклона линейной функции является важным показателем, который помогает понять характер и тенденции этих процессов. Кроме того, зная коэффициент наклона, можно проводить дальнейшие расчеты и предсказывать будущие значения функции.
Определение и основные характеристики

Коэффициент наклона обозначается буквой k и определяется как отношение приращения значений функции к соответствующему приращению аргумента. Коэффициент наклона может быть положительным, отрицательным или нулевым.
Если коэффициент наклона положителен, это означает, что функция возрастает: с увеличением значения аргумента, значение функции также увеличивается. Если коэффициент наклона отрицателен, это означает, что функция убывает: с увеличением значения аргумента, значение функции уменьшается. В случае, когда коэффициент наклона равен нулю, функция горизонтальна и не изменяется при изменении аргумента.
Примеры и график линейной функции
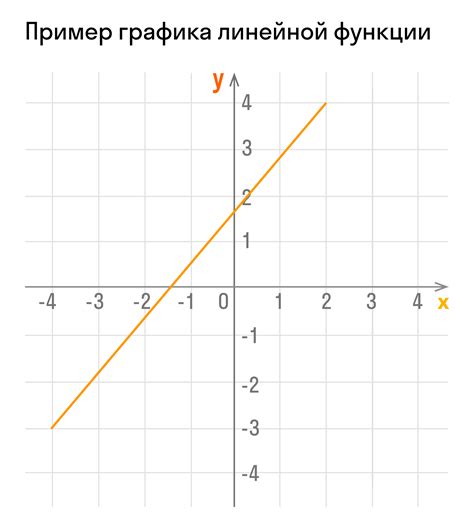
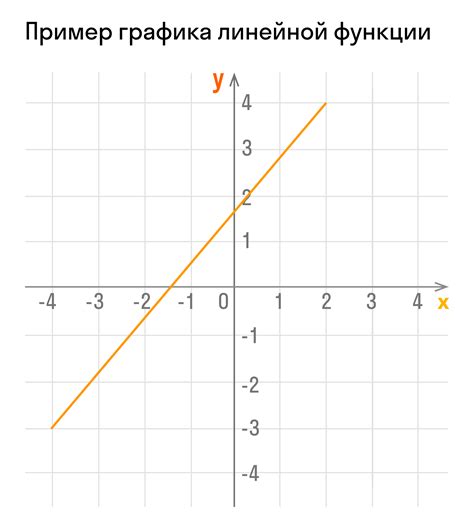
Рассмотрим несколько примеров линейных функций и их графиков, чтобы лучше понять, как они выглядят и как они могут быть использованы.
Пример 1:
Рассмотрим функцию f(x) = 2x + 1.
Эта функция имеет коэффициент наклона 2 и сдвиг по y-оси равный 1. Значит, она будет иметь наклон вверх и проходить через точку (0,1). С увеличением x на 1, значение функции f(x) увеличивается на 2. График этой функции будет прямой линией, проходящей через точку (0,1) и имеющей наклон вверх.
График функции будет выглядеть следующим образом:
Вставить сюда изображение графика функции f(x) = 2x + 1
Пример 2:
Рассмотрим функцию g(x) = -3x + 4.
Эта функция имеет коэффициент наклона -3 и сдвиг по y-оси равный 4. Значит, она будет иметь наклон вниз и проходить через точку (0,4). С увеличением x на 1, значение функции g(x) уменьшается на 3. График этой функции будет прямой линией, проходящей через точку (0,4) и имеющей наклон вниз.
График функции будет выглядеть следующим образом:
Вставить сюда изображение графика функции g(x) = -3x + 4
Это лишь некоторые примеры линейных функций и их графиков. В реальной жизни линейные функции могут быть использованы для моделирования различных явлений, таких как зависимость продаж от времени или изменение температуры в течение дня.
Коэффициент наклона
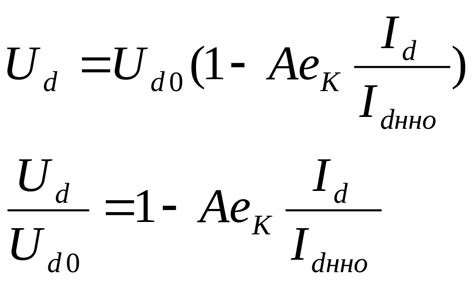
Коэффициент наклона обычно обозначается буквой "k" и рассчитывается по формуле:
k = (y2 - y1) / (x2 - x1)
где (x1, y1) и (x2, y2) - координаты двух точек на графике функции.
Значение коэффициента наклона может быть положительным, отрицательным или нулевым. Если коэффициент больше нуля, то график функции возрастает (увеличивается), если он меньше нуля, то график функции убывает (уменьшается), а если коэффициент равен нулю, то график функции параллелен оси OX и не меняется.
Коэффициент наклона также может быть использован для определения скорости изменения значения функции. Чем больше значение коэффициента, тем быстрее меняется значение функции при изменении аргумента. Например, если коэффициент наклона равен 2, то значение функции увеличивается в два раза при каждом изменении аргумента на единицу.
Изучение и анализ коэффициента наклона помогает более глубоко понять свойства линейной функции и ее поведение на графике. Это позволяет применять эту информацию для решения различных задач, в том числе в экономике, физике, математике и других областях.
Определение и связь с линейной функцией
Формально, коэффициент наклона линейной функции, обозначаемый как m, определяется как отношение изменения значения y (выходной переменной) к изменению значения x (входной переменной) в линейном уравнении y = mx + b, где b - свободный член.
Значение коэффициента наклона представляет собой тангенс угла наклона прямой линии, которую задает линейная функция. Если коэффициент наклона положителен, то линия наклонена вверх, а если он отрицателен, то линия наклонена вниз.
Коэффициент наклона играет важную роль при анализе данных и построении прогнозов. Он позволяет определить направление и интенсивность взаимосвязи между двумя переменными. Например, если коэффициент наклона равен 2, то каждое изменение переменной x на 1 приведет к изменению переменной y на 2.
В математических и физических моделях коэффициент наклона используется для описания закономерностей и прогнозирования значений переменных. Он помогает установить связь между различными явлениями и определить влияние факторов на эти явления.
Способы расчета коэффициента наклона

Коэффициент наклона линейной функции, также известный как угловой коэффициент, показывает, насколько быстро меняется значение функции относительно изменения ее аргумента. Существует несколько способов рассчитать коэффициент наклона:
1. Графический метод
На координатной плоскости строится график линейной функции. Затем находят две точки на графике и определяют их координаты. После этого вычисляют разность значений функции и разности соответствующих аргументов. Коэффициент наклона равен отношению разности значений функции к разности аргументов.
2. Формулы
Если известны координаты двух точек на графике линейной функции, можно воспользоваться формулой для расчета коэффициента наклона:
m = (y2 - y1) / (x2 - x1)
где m - коэффициент наклона, (x1, y1) и (x2, y2) - координаты двух точек на графике.
Зная уравнение линейной функции вида y = mx + b, где b - свободный член, можно использовать другую формулу:
m = (y - y1) / (x - x1)
где m - коэффициент наклона, (x1, y1) - любая точка на графике, x и y - координаты другой точки на графике.
3. Метод наименьших квадратов
Если имеется набор данных, который представляет пары значений функции и соответствующих аргументов, можно воспользоваться методом наименьших квадратов для расчета коэффициента наклона. Этот метод позволяет найти наилучшую прямую, которая приближает эти данные. Расчеты выполняются с использованием специальных математических формул.
Рассчет коэффициента наклона
Чтобы рассчитать коэффициент наклона линейной функции, необходимо использовать формулу:
коэффициент наклона = (Y2 - Y1) / (X2 - X1)
где Y1 и Y2 - значения зависимой переменной на двух разных точках, а X1 и X2 - значения независимой переменной на этих точках.
Шаги для рассчета:
- Выберите две точки на графике линейной функции.
- Запишите значения X и Y для каждой точки.
- Подставьте значения в формулу и вычислите коэффициент наклона.
Пример рассчета:
- Пусть у нас есть график линейной функции, проходящий через точки (2, 4) и (6, 10).
- Запишем значения X и Y для этих точек: X1 = 2, Y1 = 4, X2 = 6, Y2 = 10.
- Подставим значения в формулу и рассчитаем коэффициент наклона: коэффициент наклона = (10 - 4) / (6 - 2) = 6 / 4 = 1.5
Таким образом, коэффициент наклона этой линейной функции равен 1.5.
Использование коэффициента наклона позволяет предсказывать значения зависимой переменной и анализировать тенденции в данных. Также он может быть полезен при создании математических моделей и прогнозировании будущих значений.