Понятие коэффициента подобия площадей треугольников является важной частью геометрии и находит применение в различных областях науки и техники. Он позволяет определить, насколько близко два треугольника по площади при заданных условиях. В данном руководстве мы рассмотрим различные методы и формулы, которые помогут вам вычислить коэффициент подобия площадей треугольников.
Методы вычисления коэффициента подобия площадей треугольников разнообразны и могут быть применены в различных ситуациях. Один из самых распространенных методов основан на использовании соотношения длин сторон треугольников. Другой метод основан на использовании площадей треугольников и позволяет определить точную величину коэффициента подобия.
Для вычисления коэффициента подобия площадей треугольников необходимо учесть такие параметры, как длины сторон, высоты, радиусы вписанных и описанных окружностей и другие. Различные формулы, основанные на геометрических свойствах треугольников, позволяют найти нужные значения и дальше использовать их для расчета коэффициента подобия.
В данном руководстве мы представим вам подробное объяснение каждого из методов вычисления коэффициента подобия площадей треугольников. Мы рассмотрим как основные, так и более сложные формулы, что позволит вам выбрать наиболее подходящий метод в зависимости от задачи. При использовании данного руководства вы сможете с легкостью вычислять коэффициент подобия треугольников и применять его в своей работе или исследованиях.
Что такое коэффициент подобия площадей треугольников?

Расчет коэффициента подобия площадей треугольников основывается на формуле: коэффициент подобия площадей треугольников = (площадь первого треугольника) / (площадь второго треугольника).
Если значение коэффициента подобия площадей треугольников равно 1, то треугольники абсолютно подобны друг другу, то есть имеют одинаковую площадь. Если значение коэффициента меньше 1, то площадь второго треугольника меньше площади первого, и они не подобны. Если значение коэффициента больше 1, то площадь второго треугольника больше площади первого, и они также не подобны.
Коэффициент подобия площадей треугольников является важным инструментом в геометрии и может быть использован в различных задачах, включая нахождение пропорций между сторонами и площадями треугольников, нахождение подобных треугольников в сложных фигурах или применение в различных инженерных расчетах.
Определение коэффициента подобия треугольников
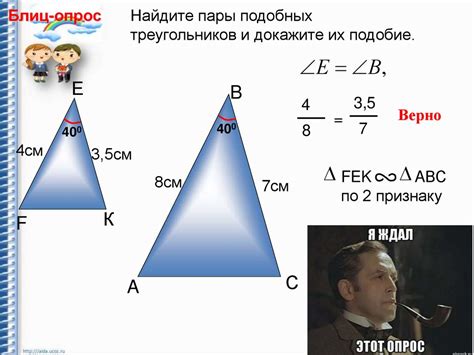
Для определения коэффициента подобия треугольников применяются различные методы и формулы. Один из самых распространенных методов – это сравнение соответствующих сторон треугольников и сравнение соответствующих углов.
Если все соответствующие стороны треугольников пропорциональны и все соответствующие углы равны, то треугольники считаются подобными. В этом случае коэффициент подобия равен 1.
Коэффициент подобия также может быть выражен через площади треугольников. Если площади треугольников пропорциональны квадратам соответствующих сторон, то треугольники считаются подобными. В этом случае коэффициент подобия равен квадратному корню из отношения площадей.
Для вычисления коэффициента подобия треугольников можно использовать формулу:
| Формула | Значение |
|---|---|
| Коэффициент подобия | sqrt(S1 / S2) |
где S1 и S2 – площади соответствующих треугольников.
Методы вычисления коэффициента подобия
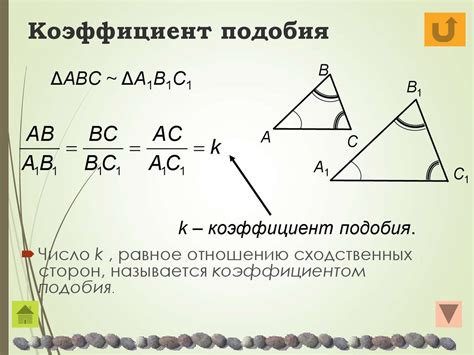
Метод сравнения длин сторон. В этом методе, длины сторон двух треугольников сравниваются. Если отношение длин сторон одного треугольника к длинам соответствующих сторон другого треугольника одинаково для всех сторон, то треугольники считаются подобными.
Метод сравнения углов. В этом методе, углы треугольников сравниваются. Если все углы одного треугольника равны соответствующим углам другого треугольника, то треугольники считаются подобными.
Метод сравнения площадей. В этом методе, площади треугольников сравниваются. Если отношение площади одного треугольника к площади другого треугольника равно квадрату отношения длин сторон треугольников, то треугольники считаются подобными.
Формула коэффициента подобия. Формула для вычисления коэффициента подобия двух треугольников:
Коэффициент подобия = (длина стороны треугольника 1 / длина стороны треугольника 2) × (длина стороны треугольника 2 / длина стороны треугольника 1) = (площадь треугольника 1 / площадь треугольника 2) × (площадь треугольника 2 / площадь треугольника 1)
Выбор метода вычисления коэффициента подобия треугольников зависит от поставленной задачи и доступных данных о треугольниках.
Формула коэффициента подобия площадей треугольников
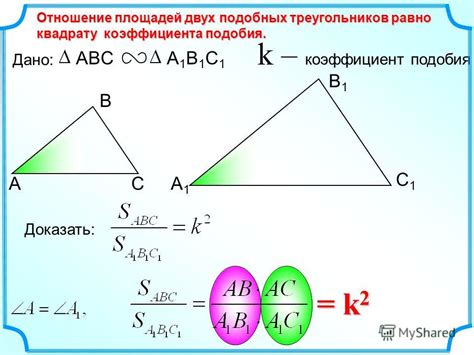
Коэффициент подобия площадей треугольников используется для определения степени подобия двух треугольников. Этот коэффициент представляет собой отношение площади одного треугольника к площади другого треугольника.
Формула для расчета коэффициента подобия площадей треугольников имеет вид:
| Площадь первого треугольника | Площадь второго треугольника |
| Коэффициент подобия площадей = ------------------------ | ---------------------------------------- |
| Площадь второго треугольника | Площадь первого треугольника |
В данной формуле необходимо вычислить площади обоих треугольников и затем полученные значения вставить в соответствующие места. Первая строка в таблице представляет собой площадь первого треугольника, вторая строка - площадь второго треугольника, третья строка - коэффициент подобия площадей.
Результатом расчета коэффициента подобия площадей треугольников будет число, которое показывает, насколько меньше или больше площадь одного треугольника по сравнению с площадью другого треугольника. Если коэффициент подобия равен 1, то треугольники полностью подобны, а если он больше или меньше 1, то имеется соответственно увеличение или уменьшение площади треугольника.
Почему коэффициент подобия площадей важен?

Понимание коэффициента подобия площадей имеет несколько важных практических применений. Во-первых, он используется в геометрии для нахождения подобных треугольников. Известность этого коэффициента помогает нам сравнивать и классифицировать треугольники по их степени подобия. Это позволяет нам легче работать с треугольниками, измерять их характеристики и применять эту информацию в решении задач.
Кроме того, коэффициент подобия площадей может быть использован для решения проблем, связанных с масштабированием. Например, если у нас есть большой треугольник и нам нужно создать его уменьшенную копию, мы можем использовать коэффициент подобия площадей, чтобы определить правильные пропорции для уменьшенного треугольника. Это помогает нам сохранить соответствие между оригинальным и уменьшенным треугольниками.
Коэффициент подобия площадей позволяет нам также сравнивать формы различных треугольников. С его помощью мы можем выявить сходства и различия между треугольниками, а также изучать их свойства и характеристики. Это важно для областей, таких как архитектура, дизайн и искусство, где подобие форм играет важную роль.
Таким образом, понимание и использование коэффициента подобия площадей является неотъемлемой частью изучения геометрии и имеет широкий спектр применений. Этот показатель помогает нам анализировать треугольники, определять их подобие и использовать эту информацию для решения различных задач, связанных с геометрией и масштабированием.
Примеры применения коэффициента подобия площадей
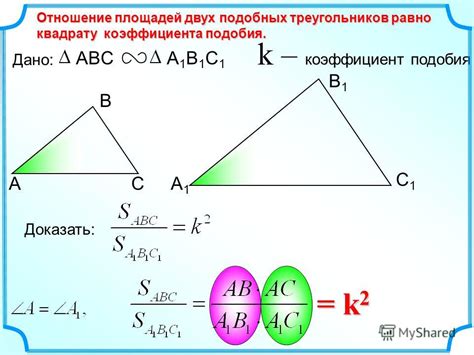
Коэффициент подобия площадей треугольников используется в различных областях, где необходимо установить соотношение площадей между треугольниками. Ниже приведены несколько примеров его применения.
- Геометрия. Коэффициент подобия площадей позволяет определить, насколько два треугольника похожи друг на друга. Это важно при анализе геометрических фигур или при решении задач на подобие треугольников.
- Статистика. Коэффициент подобия площадей может быть использован для сравнения различных групп или выборок. Например, если требуется сравнить площади аграрных угодий в разных регионах, можно использовать коэффициент подобия площадей, чтобы определить, насколько эти угодья похожи друг на друга в терминах площадей.
- Архитектура. В архитектуре коэффициент подобия площадей может быть полезен при планировании зданий или городской застройки. Если, например, архитектору требуется определить, какой размер должны иметь окна в здании, чтобы сохранить гармоничное соотношение с общей площадью фасада, он может использовать коэффициент подобия площадей, чтобы найти подходящие пропорции.
- Физика. В физике коэффициент подобия площадей может быть использован для анализа законов сохранения энергии или массы. Например, при изучении падения предметов в воздухе, можно использовать коэффициент подобия площадей, чтобы определить, насколько воздушное сопротивление влияет на движение разных объектов.
Вычисление коэффициента подобия площадей в реальных задачах
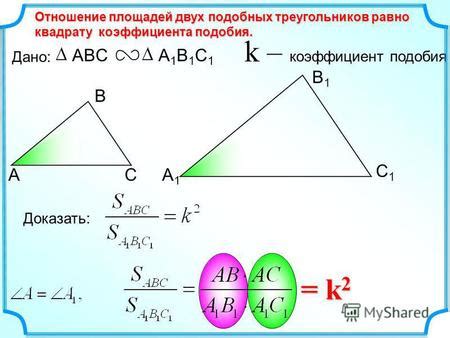
Рассмотрим реальный пример использования коэффициента подобия площадей. Представим себе ситуацию, когда мы хотим создать модель огорода, копирующую форму и площадь настоящего огорода. Мы можем измерить площадь настоящего огорода и получить некую числовую величину. Затем, создавая модель огорода, мы можем вычислить её площадь и сравнить её с площадью настоящего огорода.
Если коэффициент подобия площадей примерно равен единице, то это означает, что модель огорода по площади подобна настоящему огороду. Если же коэффициент подобия площадей значительно отличается от единицы, то это может говорить о том, что модель огорода не точно копирует площадь настоящего огорода.
Определение коэффициента подобия площадей треугольников основано на применении формулы:
Коэффициент подобия площадей (КП) = (Площадь треугольника 1 / Площадь треугольника 2)
Существуют различные методы и приближенные формулы для вычисления площади треугольника, их можно использовать в зависимости от доступных данных и точности, которую требуется достичь. Одним из самых популярных методов является формула Герона.
Вычисление коэффициента подобия площадей треугольников в реальных задачах помогает определить степень сходства или различия между треугольниками на основе их площадей. Это важная задача в геометрии, которая находит применение в различных областях, таких как архитектура, строительство, дизайн и другие.
Правильное вычисление коэффициента подобия площадей треугольников позволяет получить более точные результаты при сравнении и анализе геометрических объектов. В сочетании с другими методами и инструментами геометрии, этот коэффициент может быть полезным средством для решения различных задач и принятия важных решений.
Ограничения и ошибки при вычислении коэффициента подобия площадей
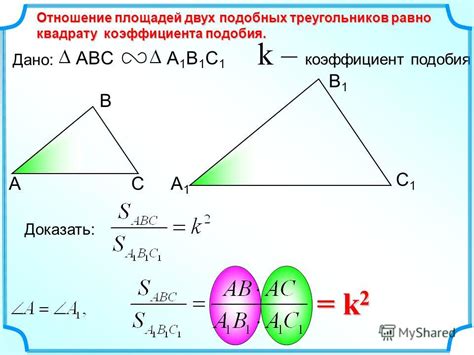
При вычислении коэффициента подобия площадей треугольников необходимо учитывать некоторые ограничения и возможные ошибки, которые могут возникнуть при использовании методов и формул.
Во-первых, следует отметить, что коэффициент подобия площадей может быть вычислен только для двух подобных треугольников. Если треугольники не являются подобными, то вычисление такого коэффициента не имеет смысла.
Во-вторых, при использовании формулы для вычисления площади треугольника необходимо быть осторожным при подсчёте длин сторон и высоты треугольника, так как даже небольшая погрешность в измерениях может привести к значительной ошибке в вычислении площади.
Также следует помнить о том, что вычисление коэффициента подобия площадей треугольников требует точного определения соответствующих сторон и высот, а также углов. Если имеются неточности в данных или неправильно определены параметры треугольников, то результаты вычислений будут некорректными и не достоверными.
Важно также учитывать, что коэффициент подобия площадей является отношением площадей треугольников и не содержит информации о пропорциональности сторон или углов треугольников. Это следует учитывать при интерпретации результатов вычислений.
Рекомендации по использованию коэффициента подобия площадей
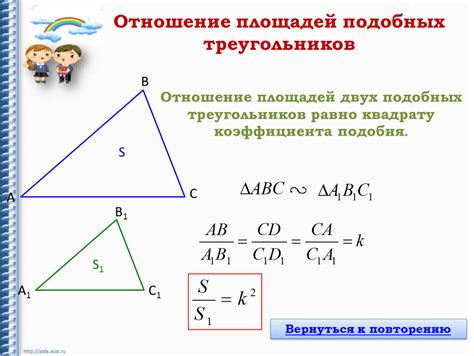
Вот несколько рекомендаций, которые помогут вам использовать коэффициент подобия площадей:
1. Правильно измеряйте площади треугольников:
Для расчета коэффициента подобия площадей необходимо правильно измерить площади треугольников. Используйте известные формулы для нахождения площадей треугольников, такие как формула Герона или формула половины произведения стороны на высоту.
2. Помните о порядке сторон:
Порядок указания сторон треугольников должен быть одинаковым при расчете коэффициента подобия площадей. Правильный порядок сторон обычно задается в условии задачи или изображении треугольников.
3. Учитывайте соответствующие стороны:
При расчете коэффициента подобия площадей необходимо учесть только соответствующие стороны треугольников. Соответствующие стороны треугольников – это стороны, которые имеют одинаковые индексы (например, сторона А треугольника 1 соответствует стороне А треугольника 2).
4. Выполняйте расчеты аккуратно:
При расчете коэффициента подобия площадей не допускайте опечаток и грамматических ошибок, так как это может привести к неправильным результатам. Будьте внимательны и проверяйте свои расчеты несколько раз.
Использование коэффициента подобия площадей является полезным при изучении геометрии и решении различных задач. Следуя данным рекомендациям, вы сможете правильно использовать этот коэффициент и получить точные результаты.