Коэффициент подобия треугольников по сторонам — методы определения и формулы расчета

Треугольники являются одной из основных фигур в геометрии и широко применяются в различных областях, начиная от строительства и конструирования до астрономии и физики. Одним из важных параметров треугольников является их подобие, которое позволяет сравнивать треугольники и находить соответствующие стороны и углы.

Коэффициент подобия треугольников по сторонам - это один из способов определить, насколько два треугольника похожи друг на друга. Основной идеей данного метода является сравнение соответствующих сторон треугольников. Если два треугольника имеют пропорциональные стороны, то они считаются подобными.

Для вычисления коэффициента подобия треугольников по сторонам существует несколько формул. Одна из наиболее распространенных формул выглядит следующим образом: коэффициент подобия равен отношению длин одних соответствующих сторон к длинам других соответствующих сторон. Например, если мы сравниваем треугольник А с треугольником В, то коэффициент подобия будет равен отношению длины стороны А к длине соответствующей стороны В.

Как определить коэффициент подобия треугольников по сторонам?

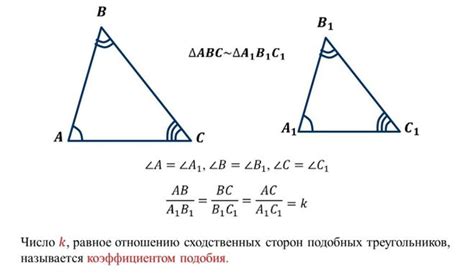
Для определения коэффициента подобия треугольников по сторонам, необходимо выполнить следующие шаги:

1. Измерить длины всех сторон первого треугольника и записать их значения.
2. Измерить длины всех сторон второго треугольника и записать их значения.
3. Вычислить отношения длин соответствующих сторон путем деления длин сторон первого треугольника на длины соответствующих сторон второго треугольника.
4. Найти среднее арифметическое от всех полученных отношений длин сторон.
5. Полученное среднее арифметическое является коэффициентом подобия треугольников по сторонам.

Если коэффициент подобия треугольников по сторонам равен 1, то треугольники считаются равными по сторонам. Если коэффициент подобия больше 1, то один треугольник является увеличенной копией другого треугольника. Если коэффициент подобия меньше 1, то треугольники будут иметь разные размеры, пропорционально сокращенные по сравнению с другим треугольником.

Таким образом, коэффициент подобия треугольников по сторонам позволяет определить, насколько треугольники подобны друг другу в размерах и форме, и является важным инструментом при изучении геометрии и нахождении подобных фигур.

Методы вычисления коэффициента подобия треугольников

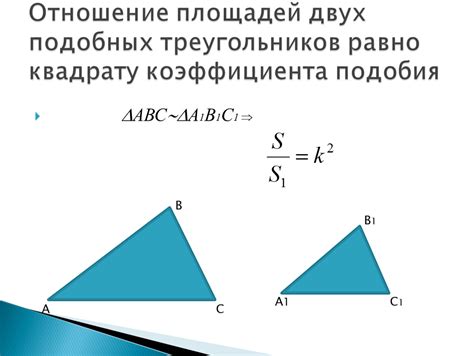
Одним из методов вычисления коэффициента подобия является метод сравнения сторон треугольников. Для этого необходимо сравнить соответствующие стороны треугольников и вычислить их отношение. Если все отношения равны между собой, то треугольники являются подобными. Этот метод основывается на теореме отношения сторон подобных треугольников.

Другим методом вычисления коэффициента подобия является метод сравнения углов треугольников. Для этого необходимо сравнить углы треугольников и вычислить их отношение. Если все отношения равны между собой, то треугольники являются подобными. Этот метод основывается на теореме отношения углов подобных треугольников.

Также существует комплексный метод вычисления коэффициента подобия, который учитывает и стороны, и углы треугольников. При этом вычисляется и сравнивается не только отношение сторон и углов, но и другие геометрические параметры треугольников, такие как площади, периметры, радиусы вписанных окружностей и т.д.

Выбор метода вычисления коэффициента подобия треугольников зависит от конкретной задачи и доступных данных. Если известны только стороны треугольников, то можно использовать метод сравнения сторон. Если известны только углы треугольников, то можно использовать метод сравнения углов. Если известны и стороны, и углы треугольников, то можно использовать комплексный метод.

Важно отметить, что коэффициент подобия треугольников не является абсолютной величиной и зависит от выбранного метода вычисления. Поэтому при сравнении треугольников следует использовать математически корректные методы и формулы.

Формула для вычисления коэффициента подобия треугольников по сторонам

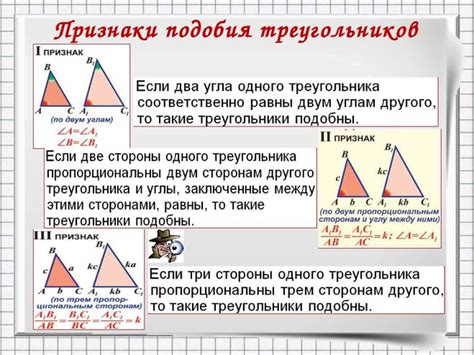
Для вычисления коэффициента подобия треугольников по сторонам используется следующая формула:

Где

• К - коэффициент подобия треугольников по сторонам;
• a₁, b₁, c₁ - длины сторон первого треугольника;
• a₂, b₂, c₂ - длины сторон второго треугольника.

Для определения подобия двух треугольников, необходимо вычислить коэффициент подобия по сторонам по формуле, и если значения всех трех дробей равны, то треугольники подобны.

Использование коэффициента подобия треугольников по сторонам позволяет сравнивать треугольники, определять их подобие и применять в геометрических задачах.

Значение коэффициента подобия треугольников и его интерпретация

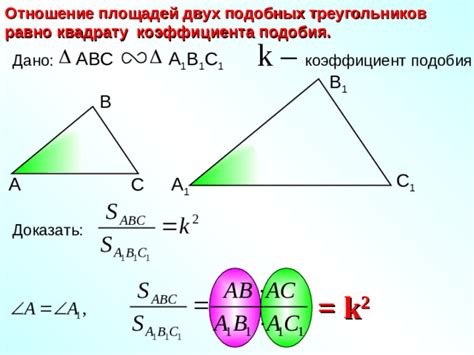
Значение коэффициента подобия треугольников находится путем сравнения длин их сторон. Формула для его вычисления выглядит следующим образом:

Коэффициент подобия = длина стороны треугольника A / длина стороны треугольника B

Значение коэффициента подобия лежит в интервале от 0 до бесконечности. Если коэффициент равен 1, это означает, что треугольники полностью подобны друг другу. Чем ближе значение коэффициента к 0, тем менее треугольники похожи друг на друга.

Интерпретация значения коэффициента подобия треугольников может быть следующей:

• Если значение коэффициента находится в интервале от 0 до 1, это означает, что треугольник B является уменьшенной копией треугольника A.
• Если значение коэффициента равно 1, это означает, что треугольники A и B являются идентичными.
• Если значение коэффициента больше 1, это означает, что треугольник B является увеличенной копией треугольника A.

Коэффициент подобия треугольников позволяет решать такие задачи, как вычисление неизвестных сторон и углов, нахождение площади и периметра подобного треугольника. Он также может использоваться в различных инженерных и архитектурных расчетах для определения масштаба моделей и проектов.

Примеры вычисления коэффициента подобия треугольников по сторонам

Для вычисления коэффициента подобия треугольников по сторонам необходимо знать длины соответствующих сторон двух треугольников. Допустим, у нас есть треугольник А с длинами сторон a₁, a₂ и a₃, и треугольник В с длинами сторон b₁, b₂ и b₃. Формула для вычисления коэффициента подобия по сторонам выглядит следующим образом:

Коэффициент подобия = (a₁/b₁) = (a₂/b₂) = (a₃/b₃)

Приведем несколько примеров вычисления коэффициента подобия треугольников по сторонам:

Пример 1:

Треугольник А: a₁ = 5, a₂ = 7, a₃ = 9.

Треугольник В: b₁ = 10, b₂ = 14, b₃ = 18.

Вычислим коэффициент подобия:

(5/10) = (7/14) = (9/18) = 0.5

Пример 2:

Треугольник А: a₁ = 3, a₂ = 4, a₃ = 5.

Треугольник В: b₁ = 6, b₂ = 8, b₃ = 10.

Вычислим коэффициент подобия:

(3/6) = (4/8) = (5/10) = 0.5

В обоих примерах мы получили одинаковое значение коэффициента подобия, что говорит о том, что треугольники А и В подобны по сторонам.