Треугольники являются одной из самых основных геометрических фигур, применяемых в различных областях науки и техники. Они обладают множеством характеристик и свойств, позволяющих проводить различные исследования и вычисления.
Один из важных аспектов изучения треугольников - это коэффициент подобия треугольников с одинаковыми сторонами. Этот коэффициент позволяет определить, насколько два треугольника с одинаковыми сторонами похожи друг на друга. Чем выше коэффициент подобия, тем более похожи треугольники.
Для определения коэффициента подобия необходимо измерить соответствующие стороны треугольников и сравнить их значения. Для этого можно использовать различные методы исследования, такие как геометрический метод, метод комплексных чисел, метод сравнения площадей и другие.
Коэффициент подобия треугольников

Для вычисления коэффициента подобия треугольников используется следующая формула:
- Найдите длину первой стороны треугольника А и треугольника В.
- Найдите длину второй стороны треугольника А и треугольника В.
- Найдите длину третьей стороны треугольника А и треугольника В.
- Разделите длины сторон треугольника А на длины соответствующих сторон треугольника В.
- Полученные результаты возведите в квадрат.
- Вычислите среднюю арифметическую последних трех результатов.
- Коэффициент подобия треугольников равен корню из полученного числа.
Коэффициент подобия треугольников может принимать значения от 0 до 1. Если коэффициент равен 0, это означает, что треугольники не подобны. Если коэффициент равен 1, это означает, что треугольники абсолютно одинаковы.
Используя коэффициент подобия треугольников, можно сравнить их формы и определить, насколько один треугольник похож на другой. Это полезно при решении задач геометрии, а также в различных областях, где требуется анализ и сравнение различных форм.
Определение исследования

В исследовании коэффициента подобия треугольников с одинаковыми сторонами применяются различные методы анализа и вычисления. Один из таких методов - метод сравнения углов треугольников. Он основывается на сравнении углов двух треугольников, чтобы определить их подобие. Если углы треугольников совпадают или очень близки по величине, то коэффициент подобия будет близким к 1, что будет указывать на высокую степень сходства треугольников. Если же углы сильно отличаются, то коэффициент будет близким к 0, что будет указывать на низкую степень сходства треугольников.
Второй метод исследования - метод сравнения длин сторон треугольников. Он основывается на сравнении длин трех сторон треугольников, чтобы определить их подобие. Если длины сторон треугольников пропорциональны, то коэффициент подобия будет близким к 1. Если же длины сторон сильно отличаются, то коэффициент будет близким к 0.
Также существуют и другие методы исследования коэффициента подобия треугольников с одинаковыми сторонами, которые могут учитывать различные параметры треугольников, включая их площади, радиусы вписанных и описанных окружностей и т.д. Использование разных методов исследования позволяет получить более полное представление о степени сходства треугольников и, следовательно, более точную оценку коэффициента подобия.
В итоге, определение исследования коэффициента подобия треугольников с одинаковыми сторонами занимает важное место в изучении данной темы и включает в себя различные методы анализа и вычисления, которые позволяют определить степень сходства треугольников и рассчитать соответствующий коэффициент подобия.
Методы определения коэффициента

Существует несколько методов определения коэффициента подобия треугольников с одинаковыми сторонами. Некоторые из них приведены в таблице ниже:
| Метод | Описание |
|---|---|
| Метод сравнения углов | Этот метод заключается в сравнении углов треугольников. Если углы одного треугольника соответственно равны углам другого треугольника, то треугольники подобны. |
| Метод сравнения сторон | Этот метод заключается в сравнении длин сторон треугольников. Если длины сторон одного треугольника пропорциональны длинам сторон другого треугольника, то треугольники подобны. |
| Метод соответствия углов | Этот метод заключается в сравнении соответствующих углов треугольников. Если соответствующие углы одного треугольника равны соответствующим углам другого треугольника, то треугольники подобны. |
| Метод сравнения площадей | Этот метод заключается в сравнении площадей треугольников. Если отношение площади одного треугольника к площади другого треугольника равно коэффициенту подобия, то треугольники подобны. |
Выбор метода определения коэффициента зависит от доступных данных о треугольниках и требуемой точности результата. Разные методы могут быть применимы в разных ситуациях, поэтому важно выбирать подходящий метод в каждом конкретном случае.
Анализ сходства треугольников
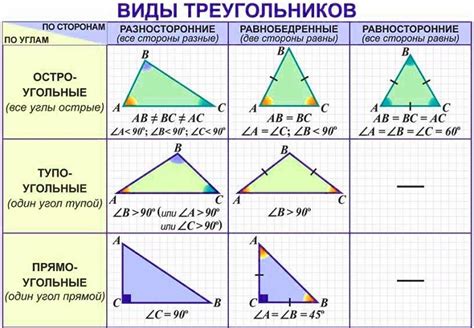
Для более глубокого понимания геометрических фигур, включая треугольники, важно иметь возможность измерять и анализировать их сходство или различие. Анализ сходства треугольников позволяет определить, насколько один треугольник похож на другой, основываясь на их свойствах и характеристиках.
Одним из основных показателей сходства треугольников является коэффициент подобия. Коэффициент подобия определяет, насколько два треугольника подобны друг другу, то есть насколько их формы и размеры совпадают.
Рассчитать коэффициент подобия треугольников можно с помощью различных методов, таких как:
- Метод сравнения сторон: сравниваются длины сторон треугольников. Если все стороны двух треугольников пропорциональны, то они подобны друг другу.
- Метод сравнения углов: сравниваются величины углов треугольников. Если все углы двух треугольников равны или пропорциональны, то они подобны друг другу.
- Метод сравнения сторон и углов: сравниваются и длины сторон, и величины углов треугольников. Если и стороны, и углы двух треугольников подобны друг другу, то они подобны по полному сходству.
Анализ сходства треугольников может быть полезным при решении задач геометрии, а также при различных приложениях, таких как построение карт, дизайн, архитектура и другие.
Практическое применение

| Область применения | Примеры |
|---|---|
| Геометрия и строительство |
|
| Биология и генетика |
|
| Компьютерное зрение и распознавание образов |
|
Таким образом, коэффициент подобия треугольников с одинаковыми сторонами имеет широкий спектр применения и является полезным инструментом для сравнения и анализа формы и структуры различных объектов в различных областях науки и техники.