Коэффициент трения - это величина, определяющая силу трения между двумя поверхностями. В физике, изучая движение тела по горизонтальной поверхности или по наклонной плоскости, мы не можем обойтись без учета силы трения. Коэффициент трения позволяет нам выразить эту силу численно и использовать для решения различных задач.
Формула для определения коэффициента трения:
f = Fтр / Fн, где f - коэффициент трения, Fтр - сила трения, Fн - нормальная реакция со стороны опоры.
Значение коэффициента трения может быть различным для различных пар материалов. Например, для металла оно может быть равно 0,5, а для дерева - 0,3. Коэффициент трения зависит от состояния поверхностей, с которыми соприкасается тело, а также от их материалов и состояния поверхностей. Величина коэффициента трения может быть определена экспериментально.
Пример использования коэффициента трения может быть следующим. Рассмотрим тело, движущееся по горизонтальной поверхности. Если известна сила трения и нормальная реакция, то с помощью формулы f = Fтр / Fн можно найти значение коэффициента трения. Зная коэффициент трения, мы можем определить какую силу нужно приложить, чтобы удержать или переместить тело.
Коэффициент трения в физике 7 класс
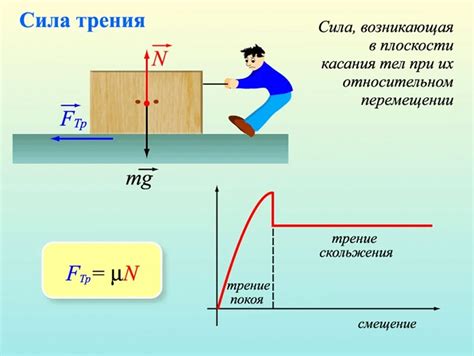
Коэффициент трения может быть разделен на две основные категории: статический коэффициент трения и кинематический коэффициент трения. Статический коэффициент трения характеризует силу трения, препятствующую началу движения между поверхностями, а кинематический коэффициент трения характеризует силу трения между поверхностями, когда они уже находятся в движении.
Формула для расчета коэффициента трения может быть записана как:
μ = F/FN
где F - сила трения, действующая между поверхностями, а FN - сила нормального давления, действующая перпендикулярно поверхности.
Примеры использования коэффициента трения в физике 7 класс могут быть связаны с исследованием трения между различными поверхностями. Например, можно провести эксперимент, чтобы определить коэффициент трения между различными видами материалов, такими как металл и дерево. Это позволит понять, как сила трения зависит от свойств материалов и силы, приложенной к поверхностям.
Формула для расчета коэффициента трения

Коэффициент трения = Сила трения / Нормальная реакция
где:
- Сила трения - сила, которая возникает между поверхностями и препятствует их скольжению;
- Нормальная реакция - сила, действующая перпендикулярно к поверхности и поддерживающая тело.
Эта формула позволяет определить величину коэффициента трения между двумя телами. Зная силу трения и нормальную реакцию, можно вычислить значение этой физической величины. Значение коэффициента трения может помочь в понимании, насколько поверхности скользкие или сцепляющиеся.
Пример:
У нас есть блок, который скользит по горизонтальной поверхности. Мы измеряем силу трения равной 20 Н и нормальную реакцию, равную 100 Н. Применяя формулу для расчета коэффициента трения, получаем:
Коэффициент трения = 20 Н / 100 Н = 0,2
Таким образом, значение коэффициента трения в данном случае равно 0,2. Это означает, что поверхности скользкие и трение между ними относительно слабое.
Определение коэффициента трения
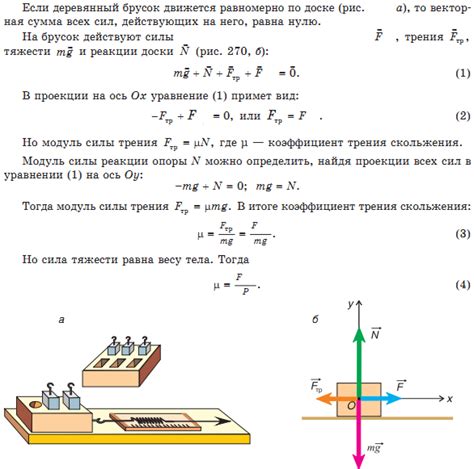
Коэффициент трения определяется отношением силы трения к силе нормального давления между поверхностями. Обозначается символом μ (мю) и может быть разным для разных материалов или состояний поверхностей.
Если поверхности движутся друг относительно друга, то говорят о динамическом (кинематическом) трении, и коэффициент трения в этом случае называется коэффициентом трения скольжения. Если поверхности находятся в состоянии покоя (не двигаются), то говорят о статическом трении, и коэффициент трения называется коэффициентом трения покоя.
Значение коэффициента трения зависит от разных факторов, таких как материалы поверхностей, их состояние (чистые или загрязненные), форма и шероховатость поверхностей и другие факторы. Величина коэффициента трения может находиться в диапазоне от 0 до 1. Коэффициент трения 0 означает отсутствие трения, а коэффициент 1 указывает на максимально возможное трение.
Определение и изучение коэффициента трения помогает понять, как взаимодействуют тела и как силы трения влияют на движение. Это позволяет решать различные задачи, связанные с движением тел, и применять эти знания в технике, строительстве и других областях.
Примеры использования коэффициента трения

Коэффициент трения важен во многих аспектах нашей жизни и имеет различные применения. Некоторые из них:
В автомобильной промышленности коэффициент трения используется для разработки шин и тормозных систем. Он помогает определить, как хорошо шины будут сцепляться с дорогой и как эффективно тормозная система будет останавливать автомобиль на мокрой или скользкой поверхности.
В инженерии коэффициент трения используется для проектирования механизмов и машин. Он помогает определить силы трения между движущимися элементами и использовать их в расчетах и конструировании, чтобы обеспечить надежную и эффективную работу устройства.
В спортивных играх и тренировках, таких как хоккей, футбол или гимнастика, коэффициент трения играет важную роль. Он определяет, как мяч или спортсмен будут взаимодействовать с поверхностью игрового поля или снаряда, а также влияет на скорость и точность движения.
В быту коэффициент трения может использоваться для выбора подходящих покрытий полов или поверхностей в разных комнатах дома или в офисе. Например, на кухне, где есть риск падения или скольжения, желательно использовать покрытия с большим коэффициентом трения, чтобы предотвратить несчастные случаи.
В строительстве коэффициент трения помогает определить, как будут взаимодействовать материалы, например, при складывании кирпичей или облицовке стен. Он влияет на качество и долговечность конструкции, а также на безопасность при выполнении работ.
Таким образом, коэффициент трения является важным параметром, который помогает в решении различных задач и принятии правильных решений во многих сферах деятельности.