Формула Бернулли и формула Пуассона являются мощными инструментами для анализа вероятностей в различных ситуациях. Они нашли широкое практическое применение в различных областях, от физики и техники до экономики и медицины. Понимание того, когда использовать каждую из этих формул, может помочь нам более точно определить вероятность различных событий.
Формула Бернулли представляет собой инструмент для анализа вероятности успеха или неудачи в серии независимых экспериментов. Она основана на предположении о постоянной вероятности успеха в каждом эксперименте. Например, когда нам нужно определить вероятность получения головы в серии подбрасываний монеты или вероятность получения определенного результата при броске кубика, мы можем использовать формулу Бернулли.
С другой стороны, формула Пуассона применяется для оценки вероятности событий, которые происходят в случайном порядке в течение определенного промежутка времени или пространства. Эта формула основана на предположении о равномерном распределении событий во времени или пространстве. Например, когда мы хотим определить вероятность того, что определенное число событий произойдет в определенный промежуток времени или пространства, мы можем использовать формулу Пуассона.
Конечно, эти формулы имеют свои ограничения и предположения, которые мы должны учитывать при их применении. Однако правильное использование формул Бернулли и Пуассона может дать нам ценную информацию о вероятностях различных событий и помочь в принятии решений на основе этой информации. Понимание того, когда применять каждую из этих формул, является ключевым навыком для аналитиков и исследователей в различных областях.
Когда использовать формулу Бернулли и Пуассона: 4 примера и применение

Примером использования формулы Бернулли может быть анализ результатов серии медицинских тестов. К примеру, если у нас есть данные о проценте ложноположительных и ложноотрицательных результатов теста, мы можем использовать формулу Бернулли для расчета вероятности правильного диагноза.
Второй пример использования формулы Бернулли - моделирование результатов эксперимента с подбрасыванием монеты. С помощью формулы Бернулли можно предсказать, сколько раз выпадет определенная сторона монеты после нескольких подбрасываний.
Формула Пуассона, с другой стороны, применяется для моделирования случайных событий с известной средней интенсивностью. Она может использоваться для расчета вероятности того, что в заданном временном интервале произойдет определенное количество событий.
Один из примеров применения формулы Пуассона - может быть прогнозирование количества звонков в службу поддержки за определенный промежуток времени. Зная среднее число звонков в день и длительность рабочего дня, мы можем использовать формулу Пуассона для определения вероятности получения определенного количества звонков.
Второй пример применения формулы Пуассона - анализ вероятности возникновения аварий или несчастных случаев в определенном месте или на определенном участке дороги. Используя исторические данные о происшествиях и среднюю интенсивность происшествий, можно оценить вероятность возникновения определенного количества происшествий за определенный период времени.
Формулы Бернулли и Пуассона позволяют сделать рациональные предсказания и прогнозы на основе статистических данных и вероятностных моделей. Они могут быть полезными инструментами в различных областях, включая медицину, финансы, науку и технику.
Вероятность успеха или неудачи в серии независимых испытаний

Формула Бернулли и формула Пуассона предназначены для расчета вероятности успеха или неудачи в серии независимых испытаний. Эти формулы применяются во многих областях, где важно определить вероятность наступления определенного события.
Формула Бернулли используется в ситуациях, когда вероятность успеха в каждом испытании остается постоянной. Она позволяет определить вероятность наступления успеха в серии из n испытаний. Формула Бернулли выглядит следующим образом:
P(X=k) = C(n, k) * p^k * (1-p)^(n-k)
где P(X=k) - вероятность, что успех наступит k раз, С(n, k) - количество сочетаний из n по k, p - вероятность успеха в каждом испытании, (1-p) - вероятность неудачи в каждом испытании.
Формула Пуассона, в свою очередь, используется в ситуациях, когда вероятность успеха в каждом испытании может изменяться или быть очень мала. Она позволяет приближенно определить вероятность успеха в серии большого числа испытаний. Формула Пуассона записывается следующим образом:
P(X=k) ≈ (λ^k * e^(-λ)) / k!
где P(X=k) - вероятность, что успех наступит k раз, λ - среднее число успехов в серии, e - математическая константа, k! - факториал числа k.
Использование формул Бернулли и Пуассона позволяет определить вероятность успеха или неудачи в серии независимых испытаний, что является важным инструментом в анализе данных и прогнозировании вероятностей различных событий.
Распределение числа событий за фиксированный период времени
Формулы Бернулли и Пуассона широко используются для анализа и моделирования случайных событий и их вероятности в различных областях, включая статистику и теорию вероятностей.
Когда речь идет о подсчете числа событий, произошедших за определенный период времени, формула Бернулли применяется в тех случаях, когда события могут происходить только в двух возможных состояниях: успех или неудача. Например, подсчет числа успешных запусков ракеты или число дефектов в производственной линии.
Формула Бернулли позволяет вычислить вероятность того, что в заданном числе испытаний произойдет определенное количество успехов и неудач. Она основывается на биномиальном распределении и принимает во внимание вероятность успеха и неудачи при каждом испытании, а также общее число испытаний.
С другой стороны, формула Пуассона применяется для расчета вероятности наступления определенного числа событий, когда число возможных состояний может быть бесконечным или очень большим. Например, подсчет числа прихода посетителей в магазине за час или число звонков в службу поддержки за день.
Формула Пуассона основана на экспоненциальном распределении и использует среднее число событий за фиксированный период времени, чтобы определить вероятность конкретного числа событий. Она полезна в случаях, когда события происходят редко или случайно, и общее число событий велико.
| Формула | Предположения | Применение |
|---|---|---|
| Формула Бернулли | - События имеют только два возможных состояния - Вероятность успеха и неудачи при каждом испытании постоянна - Число испытаний задано | - Подсчет вероятности определенного числа успехов и неудач - Моделирование бинарных событий - Прогнозирование доли успехов и неудач |
| Формула Пуассона | - Число возможных состояний велико или бесконечно - Число событий происходит случайно или редко - Среднее число событий за фиксированный период времени задано | - Подсчет вероятности конкретного числа событий - Моделирование случайных событий - Прогнозирование числа событий за фиксированный период времени |
Анализ надежности системы
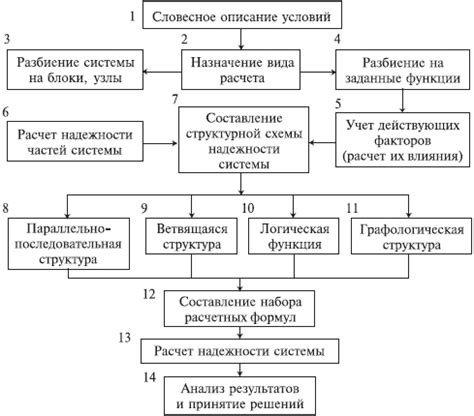
Формула Бернулли и формула Пуассона широко используются при анализе надежности системы. Надежность системы определяется способностью системы функционировать без сбоев или отказов в течение определенного времени или на определенное количество испытаний.
Формула Бернулли позволяет оценить вероятность наступления конкретного события при наличии двух возможных исходов: успеха и неудачи. Применение данной формулы позволяет оценить вероятность отказа системы при наличии известной вероятности отказа каждого из элементов.
Формула Пуассона, в свою очередь, используется для анализа вероятности наступления события в определенный момент времени или в течение определенного интервала времени. Эта формула позволяет рассчитать вероятность отказов в системе, зная среднее количество отказов за определенный промежуток времени и интенсивность отказов.
Анализ надежности системы с использованием формул Бернулли и Пуассона позволяет прогнозировать вероятность отказов системы, оптимизировать ее работу и принимать решения по повышению ее надежности. Это особенно важно в таких областях, как авиастроение, энергетика, телекоммуникации и др., где отказ системы может иметь серьезные последствия.
При анализе надежности системы необходимо учитывать различные факторы, такие как надежность отдельных элементов системы, вероятность отказа системы в целом, время работы системы, среднее время между отказами и т. д. Применение формул Бернулли и Пуассона позволяет учесть эти факторы и провести качественный анализ надежности системы.
Моделирование случайных явлений в финансовой математике

Для моделирования случайных явлений в финансовой математике часто используются формулы Бернулли и Пуассона. Формула Бернулли применяется для моделирования бинарных событий, где событие может произойти или не произойти. Результат события определяется вероятностью его возникновения и числом испытаний. Например, использование формулы Бернулли позволяет рассчитать вероятность успеха или неудачи в опционной торговле или вероятность прибыльных сделок на валютном рынке.
Формула Пуассона используется для моделирования случайных событий, которые могут произойти в течение определенного временного интервала. Эта формула учитывает интенсивность событий и позволяет рассчитать вероятность их возникновения. Например, формула Пуассона может быть применена для оценки вероятности возникновения форс-мажорных событий, таких как стихийные бедствия или политические кризисы, при оценке рисков в инвестиционных проектах или для оценки страховых премий.
Моделирование случайных явлений в финансовой математике с использованием формул Бернулли и Пуассона позволяет финансовым аналитикам и трейдерам оценить вероятность различных событий, прогнозировать риски и принимать обоснованные решения в условиях неопределенности. Надежные модели, основанные на математических формулах, помогают управлять рисками и повышать эффективность финансовых операций.