Начальная и делительная окружности - это два важных понятия в геометрии, которые часто используются при решении различных задач. Но что происходит, когда эти окружности совпадают? В этой статье мы рассмотрим основные аспекты этого явления и приведем несколько примеров для наглядности.
Когда начальная и делительная окружности совпадают, это означает, что радиусы этих окружностей одинаковые. Это основное свойство, которое определяет их взаимоотношения и влияет на решение геометрических задач. При совпадении начальной и делительной окружностей, можно сказать, что объект или точка находится на окружности с заданным радиусом.
Одним из примеров, где совпадают начальная и делительная окружности, является задача о построении равнобедренного треугольника. В этой задаче требуется построить треугольник, у которого две стороны равны. Для решения этой задачи можно использовать делительную окружность, чтобы определить точку пересечения двух радиусов и, таким образом, определить координаты вершин равнобедренного треугольника.
Другим примером, где совпадают начальная и делительная окружности, является задача о построении прямоугольника с заданным периметром и наибольшей площадью. В этой задаче может быть использована начальная окружность для определения вершин прямоугольника и делительная окружность для определения его длины и ширины.
Начальная и делительная окружности: основы и примеры
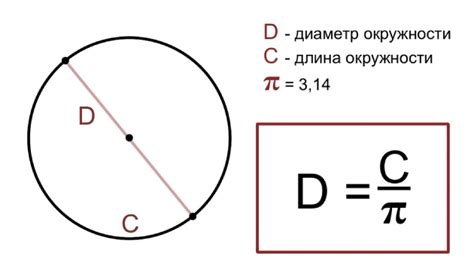
Начальная окружность - это окружность, заданная с самого начала, которая является основной вращающейся окружностью при решении задачи. Она имеет центр и радиус, которые определяют ее положение и размеры. Начальная окружность может быть задана геометрически, аналитически или каким-либо другим способом, в зависимости от конкретной задачи.
Делительная окружность - это окружность, которая совпадает с начальной окружностью и используется для деления ее на равные части. Она также имеет центр и радиус, которые совпадают с центром и радиусом начальной окружности. Делительная окружность может быть требуемой окружностью при решении определенных задач, например, при нахождении точек пересечения окружностей или деления окружности на равные сегменты.
Для понимания концепции начальной и делительной окружностей рассмотрим пример. Предположим, у нас есть задача построить две окружности, пересекающиеся в двух точках. Мы можем выбрать любую начальную окружность с определенным радиусом и центром. Затем, чтобы найти точки пересечения, мы используем делительную окружность, которая идентична начальной окружности.
Вот как это можно сделать:
- Начните с построения начальной окружности с заданным радиусом и центром.
- Постройте делительную окружность с тем же радиусом и центром, что и начальная окружность.
- Найдите точки пересечения начальной и делительной окружностей.
Примером задачи, решаемой с использованием начальной и делительной окружностей, может быть разделение окружности на равные сегменты для создания диаграммы, деление окружности на равные участки для размещения текста в виде круговой ленты и многое другое.
Важно понимать, что начальная и делительная окружности могут совпадать в различных случаях, но это не всегда является обязательным условием. Ключевое значение имеет правильное определение радиуса и центра каждой из окружностей в зависимости от поставленной задачи.
Что такое начальная и делительная окружности?

В геометрии существует понятие начальной и делительной окружности, которые играют важную роль при решении различных задач.
Начальная окружность - это окружность, заданная центром и радиусом. Она является исходной точкой для построения других фигур и окружностей. Начальная окружность определяет базовые параметры, которые легко контролируются и изменяются.
Делительная окружность - это окружность, разделяющая начальную окружность на равные части. Начальную окружность можно разделить на любое количество равных секторов, двусекторов, трисекторов и так далее. Делительная окружность может использоваться для разделения окружности на сегменты, а также для определения точек пересечения окружностей.
Понимание и использование начальной и делительной окружностей позволяют решать множество задач в геометрии и технических науках. Эти концепции особенно полезны при построении, измерении, механике и анализе движений тел.
| Примеры использования начальной и делительной окружностей: |
|---|
| 1. Построение правильного многоугольника с использованием делительной окружности. |
| 2. Определение точек пересечения окружностей путем построения делительных окружностей. |
| 3. Построение графиков функций с использованием начальной окружности. |
| 4. Измерение углов и расстояний при помощи радиусов и секторов начальной окружности. |
Значение совпадения окружностей в геометрии
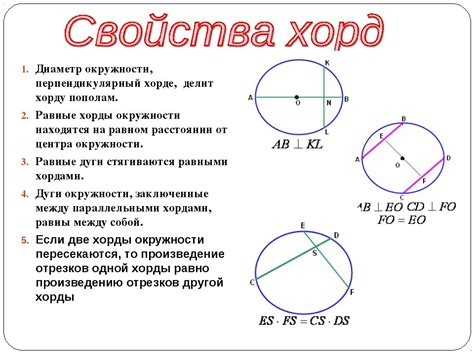
Совпадение окружностей в геометрии относится к случаю, когда начальная окружность и делительная окружность совпадают между собой. Это значит, что центры обеих окружностей совпадают, а их радиусы также одинаковы.
Совпадение окружностей имеет несколько важных аспектов в геометрии. Во-первых, это означает, что все точки на одной окружности также лежат на другой окружности. Это дает возможность использовать совпадение окружностей для нахождения точек пересечения их геометрических фигур.
Во-вторых, совпадение окружностей позволяет решать задачи, связанные с касательными. Если две окружности совпадают, то все их касательные будут одинаковыми. Это обстоятельство можно использовать для построения касательных линий и решения задач на геометрическую оптику.
И наконец, совпадение окружностей применяется при решении задач на построение геометрических фигур с использованием циркуля и линейки. Если начальная и делительная окружности совпадают, то построение требуемой фигуры будет упрощено, так как не потребуется рисовать дополнительные окружности.
Примерами совпадения окружностей в геометрии могут быть задачи на построение равностороннего треугольника, на нахождение точек пересечения окружностей и построение касательных линий. Во всех этих случаях совпадение окружностей играет важную роль при решении задачи и упрощает процесс построения.
Таким образом, совпадение окружностей имеет значительное значение в геометрии и широко применяется при решении различных задач, связанных с построением геометрических фигур и нахождением точек пересечения. Понимание совпадения окружностей позволяет геометрам использовать эту особенность в своих решениях и получать более точные и эффективные результаты.
Примеры совпадения начальной и делительной окружностей

Совпадение начальной и делительной окружностей в геометрии встречается не так часто, как другие случаи, но всё же существуют некоторые примеры, которые стоит рассмотреть.
Пример 1: Представим, что у нас есть трапеция. Пусть основания трапеции лежат на параллельных прямых, а боковые стороны пересекаются в точке О. В данном случае, начальная окружность является описанной окружностью этой трапеции, а делительная окружность совпадает с окружностью, вписанной в данную трапецию.
Пример 2: Рассмотрим равнобедренный треугольник. Пусть основание треугольника лежит на горизонтальной прямой, а боковые стороны пересекаются в точке О. В этом случае, начальная окружность является вписанной окружностью треугольника, а делительная окружность совпадает с его описанной окружностью.
Пример 3: Возьмем правильный шестиугольник. Заметим, что радиусы начальной и делительной окружностей совпадают и равны стороне шестиугольника.
Таким образом, существует несколько примеров, когда начальная и делительная окружности совпадают, и их изучение позволяет более глубоко понять связь между этими двумя понятиями в геометрии.