Конструирование эйлеровых графов, которые не содержат эйлеровых циклов, представляет собой одну из интересных задач комбинаторики и теории графов. Эйлеров граф - это граф, в котором существует путь, проходящий по каждому ребру графа ровно один раз. Однако, существуют такие графы, которые не имеют эйлеровых циклов, то есть замкнутых путей, проходящих по каждому ребру ровно один раз.
Конструирование графов без эйлеровых циклов находит свое применение в различных областях, включая телекоммуникации, компьютерные науки и теорию сложности вычислений. Этапы конструирования включают в себя анализ структуры графа, разработку алгоритмов и методов построения таких графов, а также анализ полученных результатов.
Представление и разработка эффективных алгоритмов для конструирования эйлеровых графов без эйлеровых циклов является сложной и актуальной задачей. Этот процесс требует глубокого понимания структуры графа и его свойств. Исследователи предлагают различные методы, основанные на теории графов, с использованием матриц смежности или списков смежности, а также комбинаторные методы для построения таких графов.
Что такое эйлеровый граф?
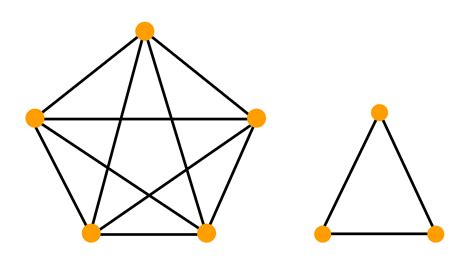
Эйлеровый граф имеет свойство, называемое эйлеровостью. Граф называется эйлеровым, если он связный и все его вершины имеют четную степень. Степень вершины определяется количеством ребер, соединенных с данной вершиной.
Эйлеровые графы являются объектами активного изучения в теории графов и находят широкое применение в различных областях, включая сетевую технологию, транспортные системы, маршрутизацию и логистику.
Для поиска эйлерового цикла в графе можно использовать различные алгоритмы, такие как алгоритм Флёри и алгоритм Хиерхоффера-Эйлера. Эти алгоритмы позволяют восстановить эйлеровый цикл или доказать его отсутствие в графе.
Существование эйлеровых графов без эйлеровых циклов

Существует две теоремы, которые определяют условия на существование графов, не содержащих эйлеровых циклов.
Первая теорема гласит, что эйлеров граф без эйлерова цикла существует тогда и только тогда, когда каждая вершина данного графа имеет четную степень.
Вторая теорема устанавливает, что эйлеров граф без эйлерова цикла существует тогда и только тогда, когда в этом графе имеются ровно две вершины, имеющие нечетную степень, и все остальные вершины имеют четную степень.
Такие графы могут использоваться для анализа и моделирования различных ситуаций, например, в сетях передачи данных, маршрутизации пакетов или планирования транспортных маршрутов. Определение существования эйлеровых графов без эйлеровых циклов позволяет решить задачи оптимального планирования и определения кратчайших маршрутов в таких сетях.
| Теорема | Условия | Существование графа |
|---|---|---|
| Первая теорема | Все вершины имеют четные степени | Граф существует |
| Вторая теорема | Ровно 2 вершины имеют нечетные степени, все остальные вершины имеют четные степени | Граф существует |
Таким образом, эйлеровые графы без эйлеровых циклов являются интересным объектом изучения в теории графов и находят применение в различных областях науки и техники.
Требования к конструированию эйлеровых графов
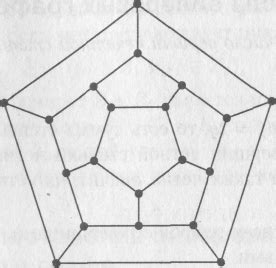
Для успешного конструирования эйлерового графа необходимо соблюдать определенные требования, которые гарантируют наличие эйлеровых циклов в графе. Вот основные требования:
| Требование | Описание |
| Связность | Граф должен быть связным, то есть между любой парой вершин должен существовать путь. |
| Четная степень вершин | Каждая вершина графа должна иметь четную степень. Если в графе есть вершина с нечетной степенью, то граф не может содержать эйлерового цикла. |
Требование связности позволяет обеспечить возможность переходить от одной вершины к другой, что является ключевым для образования эйлерового цикла. Требование четной степени вершин гарантирует, что в процессе обхода графа каждое ребро будет посещаться ровно один раз, что необходимо для формирования цикла.
Однако следует заметить, что существуют некоторые пути, которые не являются эйлеровыми, хотя удовлетворяют вышеперечисленным требованиям. Поэтому дополнительно рассматриваются и другие факторы, такие как наличие изолированных вершин или мостов, которые могут влиять на возможность образования эйлерового цикла.
Таким образом, при конструировании эйлеровых графов необходимо учитывать данные требования, чтобы гарантировать наличие эйлеровых циклов и обеспечить успешное выполнение обхода графа.
Алгоритмы для построения эйлеровых графов без эйлеровых циклов
В некоторых случаях возникает необходимость построить граф без эйлеровых циклов, но при этом сохранить его свойство эйлеровости. В таких случаях применяются специальные алгоритмы конструирования эйлеровых графов без эйлеровых циклов.
Один из таких алгоритмов называется "алгоритмом Бинома-Эйлера". Он основан на идее разделения множеств вершин графа на две группы: группу, в которой нет пары вершин с нечетными степенями, и группу, в которой есть такая пара. Затем производится процесс перестроения ребер, чтобы создать граф без эйлеровых циклов.
Алгоритм Бинома-Эйлера имеет сложность O(n^3), где n - количество вершин в графе. Он состоит из следующих шагов:
- Определить вершины с нечетными степенями и разделить их на две группы.
- Создать набор ребер между группами вершин, чтобы создать граф без эйлеровых циклов.
- Провести процесс "слияния" групп вершин до тех пор, пока не будет достигнута эйлеровость.
Второй алгоритм, называемый "алгоритмом Флёри", также позволяет построить эйлеров граф без эйлеровых циклов. Он основан на поиске "мостов" в графе и последующем их удалении.
Алгоритм Флёри имеет сложность O(n^2), где n - количество вершин в графе. Он состоит из следующих шагов:
- Найти все "мосты" в графе и записать их.
- Удалить "мосты" один за другим, образуя новые эйлеровы графы.
- Объединить все эйлеровы графы в один, чтобы получить искомый граф без эйлеровых циклов.
Выбор алгоритма зависит от особенностей задачи и требований к времени выполнения. Важно учитывать сложность алгоритма и потенциальные ограничения на размер графа.
Эйлеровы графы без эйлеровых циклов находят применение в различных областях, включая телекоммуникации, логистику, маршрутизацию и другие.
Примеры конструирования эйлеровых графов без эйлеровых циклов
При конструировании эйлеровых графов без эйлеровых циклов можно использовать различные методы. Давайте рассмотрим несколько примеров:
1. Метод добавления вершин. Начнем с пустого графа и последовательно добавляйте вершины таким образом, чтобы каждая вершина имела нечетную степень. Например, можно начать с двух вершин и добавить еще две, соединив их существующими вершинами. Затем добавьте еще две вершины и соедините их со всеми остальными. Повторяем этот процесс до тех пор, пока каждая вершина не будет иметь нечетную степень.
| Вершина | Соседние вершины |
|---|---|
| 1 | 2, 3, 4 |
| 2 | 1, 3, 5 |
| 3 | 1, 2, 6 |
| 4 | 1, 7, 8 |
| 5 | 2, 7, 9 |
| 6 | 3, 9, 10 |
| 7 | 4, 5, 11 |
| 8 | 4, 11, 12 |
| 9 | 5, 6, 12 |
| 10 | 6, 13, 14 |
| 11 | 7, 8, 14 |
| 12 | 8, 9, 15 |
| 13 | 10, 15, 16 |
| 14 | 10, 11, 17 |
| 15 | 12, 13, 17 |
| 16 | 13, 18, 19 |
| 17 | 14, 15, 19 |
| 18 | 16, 19, 20 |
| 19 | 16, 17, 18 |
| 20 | 18 |
2. Метод удаления ребер. Начнем с эйлерова графа и последовательно удаляйте ребра таким образом, чтобы конечный граф не содержал эйлеровых циклов. Например, можно начать с полного графа на 4 вершинах и последовательно удалять ребра до тех пор, пока каждая вершина не будет иметь нечетную степень.
| Вершина | Соседние вершины |
|---|---|
| 1 | 2, 3, 4 |
| 2 | 1, 3, 4 |
| 3 | 1, 2, 4 |
| 4 | 1, 2, 3 |
Таким образом, при удалении ребра между вершинами 3 и 4 получаем эйлеров граф без эйлеровых циклов.
3. Метод конвертации эйлерова цикла. Возьмем эйлеров цикл, содержащий вершину с нечетной степенью, и последовательно конвертируем его таким образом, чтобы в итоге получить эйлеров граф без эйлеровых циклов. Например, возьмем эйлеров цикл на 5 вершинах и измените его следующим образом:
| Вершина | Соседняя вершина |
|---|---|
| 1 | 2 |
| 2 | 1, 3 |
| 3 | 2, 4 |
| 4 | 3, 5 |
| 5 | 4, 1 |
Таким образом, получаем эйлеров граф без эйлеровых циклов, где степень каждой вершины равна 2.
Практическое применение эйлеровых графов без эйлеровых циклов

Эйлеровы графы без эйлеровых циклов на первый взгляд могут показаться не очень полезными, поскольку не имеют замкнутого пути, проходящего через каждое ребро графа ровно один раз. Однако, в реальной жизни есть несколько интересных ситуаций, где такие графы могут быть полезными.
Во-первых, эйлеровы графы без эйлеровых циклов могут быть использованы для моделирования ситуаций, где необходимо пройти через все ребра графа, но не требуется вернуться в исходную точку. Например, это может быть модель посещения различных адресов на карте, где человек хочет посетить все места только один раз.
Во-вторых, эйлеровы графы без эйлеровых циклов могут быть полезными в сетевом планировании и оптимизации маршрутов. Например, в транспортной логистике, где требуется доставить грузы из различных мест в другие места без возвращения к исходному месту.
Также, эйлеровы графы без эйлеровых циклов могут использоваться для создания эффективных алгоритмов поиска оптимальных маршрутов в графах. Поскольку такие графы содержат ребра, которые проходят ровно один раз, они позволяют определить оптимальные пути без необходимости повторного прохода по уже посещенным узлам.
В целом, эйлеровы графы без эйлеровых циклов могут быть полезными во множестве реальных ситуаций, где требуется решение задачи обхода графа, но без требования замкнутого пути. Понимание применимости и свойств таких графов может помочь в разработке эффективных алгоритмов и оптимизации различных процессов.
Ограничения конструирования эйлеровых графов без эйлеровых циклов

1. Число вершин
Для того чтобы конструировать эйлеров граф без эйлеровых циклов, необходимо соблюдать определенное ограничение на количество вершин графа. Вершины графа должны быть нечетным числом, иначе эйлеров граф без эйлерового цикла не может быть построен.
2. Степени вершин
Важным ограничением является степень каждой вершины графа. В эйлеровом графе без эйлерового цикла каждая вершина должна иметь четную степень. Если существует хотя бы одна вершина с нечетной степенью, то эйлеров граф без эйлерового цикла не может быть сконструирован.
3. Связность графа
Следующим ограничением является связность графа. Конструирование эйлеровых графов без эйлеровых циклов возможно только в случае, если граф является связным. Если граф состоит из нескольких компонент связности, то каждая компонента должна удовлетворять остальным ограничениям для того, чтобы построить эйлеров граф без эйлерового цикла.
4. Четность циклов
Еще одним ограничением является четность циклов графа. В случае, если граф содержит нечетные циклы, то эйлеров граф без эйлерового цикла не может быть создан. Это связано с тем, что для построения эйлерового графа без эйлерового цикла, необходимо, чтобы все циклы в графе были четными.
5. Особые случаи
Существуют некоторые особые случаи, когда даже при соблюдении вышеуказанных ограничений, эйлеров граф без эйлерового цикла не может быть построен. Это может произойти, например, когда граф содержит вершины, которые рассматриваются как "терминальные" и не могут быть посещены более одного раза.