Тригонометрические функции – одни из основных математических функций, которые широко используются в различных научных и инженерных областях. Обычно они определены на всей числовой прямой, но при решении некоторых задач возникает необходимость использования функций с модулем.
Конструирование тригонометрических функций с модулем – процесс создания новых функций на основе известных тригонометрических функций путем введения модуля. Это может быть полезно при анализе осцилляций, моделировании периодического процесса или при решении определенных задач в физике, электротехнике и других областях.
Существует несколько методов конструирования тригонометрических функций с модулем. Один из них – использование суммы или разности двух тригонометрических функций. Например, функция с модулем синуса может быть представлена как сумма синуса и модуля синуса:
Методы и примеры конструирования

Один из методов - использование свойств модуля тригонометрической функции. Например, для построения функции |cos(x)| можно использовать известное свойство: |cos(x)| = cos(x), если -π/2 ≤ x ≤ π/2, и |cos(x)| = -cos(x), если x > π/2 или x
Другим методом является использование графика базовой функции и применение операций, таких как отражение и сдвиг. Например, для построения функции |sin(x - π/2)| можно использовать базовую функцию sin(x) и применить сдвиг на π/2 влево. Затем, для получения модуля функции применяется отражение относительно оси x. Таким образом, получаем конструкцию функции |sin(x - π/2)|.
Приведенные методы и примеры помогают лучше понять процесс конструирования тригонометрических функций с модулем. Эти методы можно применять для построения других функций с модулем, а также для решения различных задач в физике, инженерии и других научных областях. Уверены, что они будут полезны в вашей работе.
Тригонометрические функции с модулем
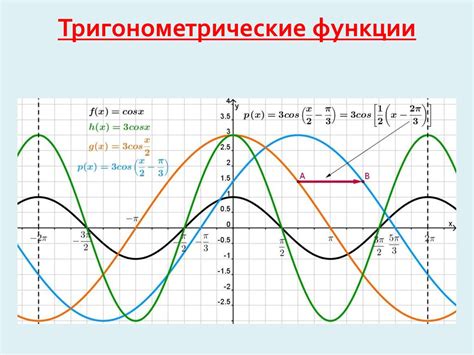
В таких ситуациях можно использовать функции с модулем. Модуль числа представляет собой абсолютное значение числа, то есть его расстояние от нуля на числовой оси.
Применение модуля к тригонометрическим функциям позволяет "обрезать" отрицательные значения и работать только с положительными результатами. Например, модуль синуса - это функция, которая возвращает абсолютное значение синуса угла.
| Функция | Определение | Диапазон значений |
|---|---|---|
| Модуль синуса | |sin(x)| | от 0 до 1 |
| Модуль косинуса | |cos(x)| | от 0 до 1 |
| Модуль тангенса | |tan(x)| | от 0 до бесконечности |
Тригонометрические функции с модулем могут быть полезны при решении задач, где требуется работать только с положительными значениями. Например, при моделировании колебаний физических систем или при построении графиков, где отрицательные значения нежелательны.
Важно отметить, что функции с модулем сохраняют основные свойства тригонометрических функций, такие как периодичность и симметрия. Однако, они могут не быть гладкими или непрерывными на всей числовой оси.
Использование функций с модулем требует аккуратности и внимательности, особенно при работе с областями значений и аргументами функций. Рекомендуется учитывать особенности модуля при проведении вычислений и интерпретации результатов.
Методы конструирования функций
Один из наиболее распространенных методов - использование графиков функций. Для этого необходимо построить график исходной функции и затем модифицировать его, применяя различные преобразования.
Еще один метод - использование тригонометрических тождеств и связей между функциями. Они позволяют выражать одну функцию через другую, что упрощает конструирование сложных функций с модулем.
Также можно использовать методы аппроксимации, которые позволяют приближенно представить тригонометрические функции с модулем в виде других, более простых функций. Это может быть полезно при численных вычислениях или приближенном аналитическом решении задач.
Конструирование функций с модулем требует хорошего понимания тригонометрии и алгебры, а также умения применять различные методы и приемы. Знание этих методов позволяет решать широкий спектр математических задач и находить новые интересные свойства тригонометрических функций.
Примеры конструирования функций
Рассмотрим несколько примеров конструирования тригонометрических функций с модулем.
Пример 1: Построим функцию синуса с модулем. Для этого можем использовать функцию:
f(x) = |sin(x)|
График данной функции будет состоять из положительной части синусоиды, отраженной от оси OX.
Пример 2: Построим функцию тангенса с модулем. Для этого можем использовать функцию:
f(x) = |tan(x)|
График данной функции будет состоять из положительной части гиперболы, ограниченной сверху нулем.
Пример 3: Построим функцию косинуса с модулем. Для этого можем использовать функцию:
f(x) = |cos(x)|
График данной функции будет состоять из положительной части косинусоиды, а затем отраженной от оси OX.
Таким образом, конструирование функций с модулем позволяет получить новые интересные графики, отличные от стандартных функций без модуля.