Треугольник – одна из самых простых и в то же время фундаментальных геометрических фигур. Эта многосторонняя геометрическая фигура состоит из трех линий, соединяющих три точки. Треугольники широко применяются не только в геометрии, но и во многих других направлениях, включая физику, инженерию и архитектуру.
Конструкция треугольника – это процесс определения его формы и размеров, основанный на заданных условиях. Существует множество способов построения треугольников, каждый из которых имеет свои собственные особенности и ограничения. Основные приемы и правила построения треугольников вытекают из свойств и установленных закономерностей этой геометрической фигуры.
Для построения треугольника важно знать его стороны и углы. Как правило, сначала задается длина одной из сторон, а затем находятся остальные стороны и углы треугольника с использованием геометрических конструкций и математических выкладок. В свою очередь, конструкции могут включать построение перпендикуляров, биссектрис, медиан и высот, а также построение параллельных линий и точек пересечения.
Основные конструкции треугольника

Существуют различные конструкции треугольника, которые основаны на определенных правилах и приемах:
- Конструкция по сторонам: по заданным длинам сторон можно построить треугольник, если выполняются условия неравенств треугольника.
- Конструкция по углам: по заданным значениям углов можно построить треугольник, если сумма углов треугольника равна 180 градусам.
- Конструкция по сторона и углу: по заданной стороне и заданному прилежащему углу можно построить треугольник, если выполняются условия неравенств треугольника.
- Конструкция по двум сторонам: по заданным длинам двух сторон и заданному значению угла между ними можно построить треугольник.
- Конструкция по высотам: можно построить треугольник, зная значения всех трех его высот.
- Конструкция по медианам: можно построить треугольник, зная значения всех трех его медиан.
- Конструкция по ортоцентру и центру описанной окружности: при условии заданного ортоцентра и центра описанной окружности можно построить треугольник.
Каждая из этих конструкций имеет свои особенности и требует соблюдения определенных условий. Знание и умение применять эти конструкции позволяют строить треугольники по заданным параметрам и решать задачи, связанные с этой геометрической фигурой.
Методы построения треугольника

Существует несколько основных методов, которые позволяют построить треугольник по заданным условиям:
| Метод | Описание |
|---|---|
| Метод сторон и углов | При данном методе известны длины всех сторон и значения всех углов треугольника. Построение осуществляется с использованием теоремы косинусов и синусов. |
| Метод сторон | При данном методе известны длины двух сторон и угол между ними. Построение осуществляется с использованием теоремы синусов. |
| Метод высот | При данном методе известны длины одной стороны и две высоты, проведенные из нее. Построение осуществляется с использованием свойств треугольника и теоремы Пифагора. |
| Метод проведения медиан | При данном методе известны длины двух сторон и медиана, проведенная из них. Построение осуществляется с использованием свойств треугольника и теоремы Пифагора. |
| Метод проведения биссектрис | При данном методе известны длины двух сторон и две биссектрисы, проведенные из них. Построение осуществляется с использованием свойств треугольника и теоремы синусов. |
Каждый из этих методов имеет свои преимущества и ограничения, в зависимости от типа задачи. Выбор метода зависит от известных данных и требуемой точности построения треугольника.
Прямоугольный треугольник: построение и особенности

Для построения прямоугольного треугольника можно использовать несколько разных методов.
- Один из самых простых способов построения прямоугольного треугольника - это использование прямой и окружности.
- Еще один метод - использование катетов: отметить на прямой две точки, которые будут являться основаниями катетов, а затем провести прямую линию, соединяющую эти точки.
- Также можно построить прямоугольный треугольник, используя гипотенузу и один из катетов: отметить на прямой точку, которая будет являться основанием катета, затем провести прямую линию, соединяющую эту точку с противоположным концом гипотенузы.
Прямоугольные треугольники встречаются во многих областях науки и техники. Например, в геометрии они используются для решения задач по тригонометрии. В строительстве они широко применяются при расчете углов и перпендикуляров. Также, прямоугольные треугольники используются в физике и электронике для построения прямоугольных координатных осей.
Равносторонний треугольник: приемы построения
1. С помощью циркуля и линейки: расставьте указатели циркуля на условных точках строительного листа, затем, не меняя расстояние между указателями, проведите дуги из каждой из точек пересечения указателей. Прямая, проходящая через вершины дуг, будет основанием треугольника. Затем, измерьте расстояние между вершинами и постройте перпендикуляры из основания каждый в свою сторону. Точками пересечения перпендикуляров с дугами являются вершины равностороннего треугольника. Соедините их линиями.
2. Через окружность: постройте окружность радиусом, равным длине стороны треугольника. Затем выберите любую точку на окружности - она станет одной из вершин треугольника. Соедините точку с центром окружности линией. Эта линия будет одной из сторон треугольника. Повторите процедуру дважды, начиная с других точек окружности, чтобы построить оставшиеся стороны треугольника.
3. С помощью деления отрезка пополам: постройте отрезок заданной длины. Затем найдите его середину и постройте перпендикулярный отрезок к нему. Длина перпендикуляра должна быть такой же, как и длина начального отрезка. Соедините концы перпендикуляра с серединой начального отрезка. Полученная линия будет одной из сторон треугольника. Повторите процедуру для построения оставшихся сторон треугольника.
Равнобедренный треугольник: основные правила
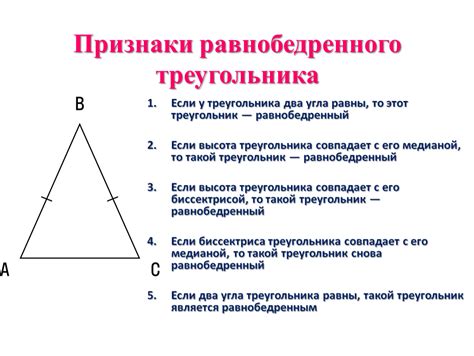
Основные правила построения равнобедренного треугольника:
| Условие | Правило |
| 1. Даны два угла и сторона между ними | Построить общую сторону и две измеренные стороны, соединить точками концы общей стороны. |
| 2. Данны две стороны и угол между ними | Построить отрезки, соединяющие концы двух измеренных сторон, и точку пересечения лежащую на отрезке, соединяющем две измеренные стороны. |
Равнобедренные треугольники часто встречаются в геометрии и находят много применений в различных областях. Зная основные правила конструирования равнобедренных треугольников, можно легко решать задачи на их построение или доказательство их свойств.
Треугольник с заданными углами: методы построения
Учитывая, что сумма углов треугольника равна 180°, мы можем определить размеры остальных углов, если заданы два из них. В основном считается, что для построения треугольника достаточно знать значения двух углов. Если известны все три угла, задача упрощается, так как можно найти длины всех сторон треугольника.
Если заданы два угла треугольника, то для построения можно использовать следующие методы:
1. Построение треугольника по известным углам методом параллельных линий:
Выберем точку A и отложим на плоскости угол, равный заданному углу α. Используем циркуль и проведем дугу радиусом AB, где A - начало угла α, а B - конец. Затем выберем точку C и отложим на плоскости угол, равный заданному углу β. Проведем дугу радиусом CB, где C - начало угла β, а B - конец. Искомая точка D будет на пересечении этих двух дуг. Для построения треугольника проведем линии AC и AD.
Примечание: этот метод основан на свойствах параллельных линий и подобия треугольников.
2. Построение треугольника по известным углам методом биссектрис:
Выберем точку A и отложим на плоскости угол, равный заданному углу α. Проведем AB - луч, делающий равные углы с двумя сторонами угла α. Затем на луче AB отложим отрезок AC, равный одной из сторон заданного угла β. Искомая точка D будет на пересечении стороны угла α и отрезка AC. Для построения треугольника проведем линии AD и DC.
Примечание: этот метод основан на свойствах биссектрис углов и подобия треугольников.
Таким образом, зная два угла треугольника, можно построить треугольник с помощью параллельных линий или биссектрис углов. Эти простые методы позволяют наглядно представить треугольник с заданными углами и отобразить его на плоскости.
Треугольник с заданными сторонами: способы построения
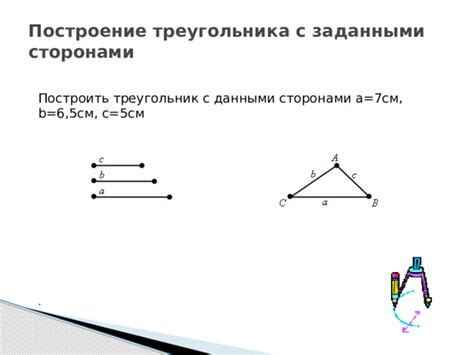
Метод 1: Используя углы. По теореме синусов можно выразить один угол треугольника через стороны. Затем, зная два угла, можно построить треугольник с помощью накладывания углов.
Метод 2: Используя высоту. Можно построить треугольник с заданными сторонами, зная хотя бы одну высоту. Для этого нужно провести высоту из одного из углов треугольника и использовать ее в качестве одной из сторон.
Метод 3: Используя медианы. Можно построить треугольник с заданными сторонами, зная хотя бы одну медиану. Для этого нужно провести медиану из одной из вершин треугольника и использовать ее в качестве одной из сторон.
Более подробные инструкции по каждому методу можно найти в специальной литературе по геометрии или в справочниках по метаматериаловедению.
| Метод | Параметры | Примечание |
|---|---|---|
| Метод 1 | Строится треугольник ABC, где AB = 5, BC = 6, AC = 7 | Углы треугольника можно накладывать с помощью угольника |
| Метод 2 | Строится треугольник ABC, где AB = 3, BC = 4, высота из угла A = 5 | Высоту можно провести с помощью циркуля и линейки |
| Метод 3 | Строится треугольник ABC, где AB = 7, медиана из вершины B = 8 | Медиану можно провести с помощью параллельного линейки |
Независимо от выбранного метода, важно строить треугольник аккуратно и точно, чтобы избежать ошибок и получить правильный результат.
Сумма углов треугольника: формула и свойства

Это свойство можно выразить математической формулой:
Сумма углов треугольника = 180°
Сумма всех трех углов в треугольнике всегда равна 180 градусам, независимо от размеров его сторон и вида треугольника.
Это свойство можно использовать для решения различных задач по геометрии. Например, если известны два угла треугольника, можно легко найти третий угол, просто вычитая сумму из 180 градусов.
Также, если известны значения двух углов, можно найти значение третьего угла, применив следующую формулу:
Значение третьего угла = 180 – (значение первого угла + значение второго угла)
Таким образом, зная сумму углов треугольника и значения двух из них, всегда можно найти значение третьего угла.