Конструирование отрезка по его координатам является одной из важных задач в геометрии. Отрезок - это прямая линия, которая соединяет две точки на плоскости. При решении этой задачи необходимо точно определить начальную и конечную точки отрезка, а также правильно построить его на плоскости.
Существует несколько методов и правил, которые позволяют конструировать отрезки по их координатам. Одним из основных методов является метод равенства отрезков по длине. Согласно этому методу, если два отрезка имеют одинаковую длину, то они равны друг другу. При конструировании отрезка по его координатам, необходимо определить его длину и сравнить ее с длиной другого отрезка.
Вторым методом является метод параллельности отрезков. Согласно этому методу, два отрезка считаются параллельными, если они имеют одинаковые коэффициенты наклона. При конструировании отрезка по его координатам, нужно определить коэффициенты наклона сторон отрезка и сравнить их, чтобы убедиться, что они параллельны.
Методы и правила

Один из методов конструирования отрезка - построение по известным координатам его концов. Для этого необходимо задать координаты начальной и конечной точки отрезка. Следующий шаг - вычисление разности координат по осям x и y каждой точки. Затем строится отрезок между двумя точками, используя полученные значения разности координат.
Правила конструирования отрезка включают использование правил треугольников, пропорции и длин отрезков. Например, для построения отрезка средней пропорциональности нужно взять отрезок и разделить его на два равных отрезка при помощи сечения. Затем из одного из концов отрезка провести прямую, перпендикулярную отрезку. Точка пересечения этой прямой и сечения будет серединой отрезка средней пропорциональности.
Другое правило - построение отрезка по заданному отношению длин. Для этого необходимо задать длину первого отрезка и отношение длин второго отрезка к первому. После чего производится конструирование отрезка в соответствии с заданными параметрами.
Важным методом конструирования отрезка является построение по заданному углу наклона и длинe отрезка. Для этого необходимо задать начальную точку, длину отрезка и угол наклона. Затем вычисляются координаты конечной точки отрезка и по ним строится сам отрезок.
Конструирование отрезка

Одним из таких методов является использование геометрических инструментов, таких как линейка и циркуль. Для построения отрезка необходимо определить начальную и конечную точки на плоскости, а затем провести линию между ними с помощью линейки.
Еще одним методом является использование координат. Для построения отрезка по координатам его конечных точек нужно определить значения координат этих точек и затем провести линию между ними. Например, если координаты начальной точки равны (x1, y1), а координаты конечной точки равны (x2, y2), то отрезок можно построить, соединив эти две точки линией.
Конструирование отрезка имеет множество практических применений, включая построение графиков функций, нахождение расстояния между точками и решение геометрических задач. О behockaи правилах конструирования отрезка по координатам важно знать при решении задач из различных областей науки и инженерии.
По координатам
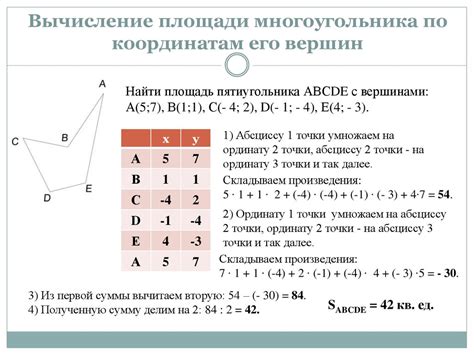
Начальная точка отрезка задается своими координатами (x1, y1), а конечная точка – своими координатами (x2, y2). Используя эти значения, можно определить длину и направление отрезка.
Длина отрезка можно вычислить по формуле sqrt((x2 - x1)2 + (y2 - y1)2). Это выражение представляет собой теорему Пифагора, где гипотенуза – это длина отрезка, а катеты – разность координат по соответствующим осям.
Направление отрезка определяется по значениям координат. Если x2 > x1 и y2 > y1, то отрезок направлен вправо и вверх. Если x2 > x1 и y2 < y1, то отрезок направлен вправо и вниз. Аналогично, если x2 < x1 и y2 > y1, то отрезок направлен влево и вверх, и если x2 < x1 и y2 < y1, то отрезок направлен влево и вниз.
Таким образом, зная координаты начальной и конечной точек отрезка, можно определить его длину и направление. Эти значения могут быть использованы для построения отрезка на координатной плоскости или для проведения других операций с отрезками.
Системы координат
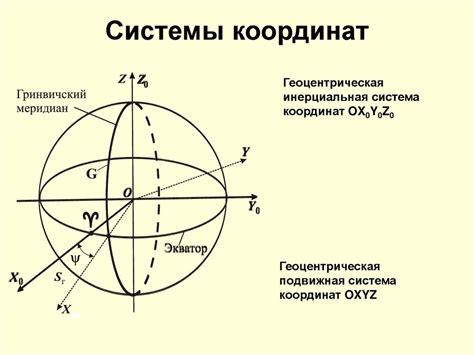
Существует несколько типов систем координат:
- Прямоугольная система координат - основана на двум перпендикулярных осях, горизонтальной (ось абсцисс) и вертикальной (ось ординат). Каждая точка задается двумя числами - абсциссой и ординатой. Прямоугольная система координат применяется для работы с плоскими объектами.
- Полярная система координат - основана на радиусе и угле, отсчитываемом от положительного направления горизонтальной оси. Точка задается двумя числами - радиусом и углом. Полярная система координат применяется для работы с круговыми объектами.
- Цилиндрическая система координат - основана на трех координатах: радиусе, угле и высоте. Точка задается тремя числами - радиусом, углом и высотой. Цилиндрическая система координат используется для работы с объектами, имеющими объемную форму.
- Сферическая система координат - основана на трех координатах: радиусе, угле азимута и угле места. Точка задается тремя числами - радиусом, углом азимута и углом места. Сферическая система координат используется для работы с географическими объектами и объектами в трехмерном пространстве.
Знание систем координат позволяет определить положение точек, строить геометрические объекты и решать различные задачи в области математики, физики, инженерии и других наук.
Абсолютные координаты
В системе абсолютных координат каждая точка на плоскости имеет свой уникальный набор координат (x, y), где x - горизонтальная координата, а y - вертикальная координата.
Для задания отрезка по абсолютным координатам необходимо указать координаты его начальной и конечной точек. Начальная точка определяется парой координат (x1, y1), а конечная точка - парой координат (x2, y2).
Пример конструирования отрезка по абсолютным координатам:
| Начальная точка | Конечная точка |
|---|---|
| (x1, y1) | (x2, y2) |
Зная начальные и конечные координаты отрезка, можно определить его длину и его угол наклона.
Абсолютные координаты являются одним из основных методов конструирования отрезков по координатам и широко применяются в графических приложениях, в том числе при создании веб-страниц с использованием языка разметки HTML.
Относительные координаты
В контексте конструирования отрезка по координатам, относительные координаты представляют собой способ задания точек или отрезков с помощью отношения к другим точкам или отрезкам в системе координат. Это позволяет гибко и удобно определять положение и размеры объектов.
Для использования относительных координат необходимо иметь изначально заданные точки или отрезки, относительно которых будут определяться новые точки или отрезки. Относительные координаты задаются в виде долей или процентов от измерений этих исходных точек или отрезков.
Например, можно задать точку на отрезке A-B с относительной координатой 0.5, что означает, что эта точка находится точно посередине между точками A и B. Для более сложных объектов, таких как многоугольники или кривые, относительные координаты позволяют определить местоположение любой точки в пределах объекта с помощью отношения к его размерам или положению других точек внутри него.
Относительные координаты находят широкое применение в графических редакторах, веб-разработке, компьютерной графике и других областях, где требуется гибкое и удобное задание положения и размеров объектов.