Прямоугольный треугольник – это треугольник, у которого один из углов равен 90 градусов. Он имеет особые свойства и широко используется в различных областях, таких как геометрия, физика, астрономия и многих других. В данной статье мы рассмотрим подробное руководство по конструкции прямоугольного треугольника по гипотенузе и катету.

Для построения прямоугольного треугольника по гипотенузе и катету нам потребуется следующее:

• Линейка: она поможет нам измерить отрезки и построить треугольник в нужном масштабе.
• Карандаш: с его помощью мы будем проводить линии и отмечать точки на листе бумаги.
• Циркуль: является необязательным инструментом, но его использование упростит процесс построения.

Приступая к построению треугольника, мы сначала отмечаем точку A, которая будет вершиной прямого угла, а затем точку B - конечную точку гипотенузы. Далее, проводим прямую AB и отмечаем на ней точку C, являющуюся конечной точкой второго катета. Полученные отрезки AB и AC будут служить основой для последующей работы.

Для завершения построения прямоугольного треугольника соединяем точки B и C, получаем прямой угол в точке A. Проверяем, что длины отрезков AB и AC соответствуют величине гипотенузы и катета. Таким образом, мы успешно построили прямоугольный треугольник по заданным гипотенузе и катету.

Подробное руководство по построению прямоугольного треугольника

Следуйте этим шагам, чтобы построить прямоугольный треугольник:

1. Выберите гипотенузу и катет, которые будут известными сторонами. Гипотенуза - это сторона прямоугольного треугольника, которая находится напротив прямого угла. Катеты - это две другие стороны треугольника.
2. Постройте основание треугольника, используя гипотенузу и один из катетов. Начните с рисования отрезка, который представляет гипотенузу, и отметьте его концы. Затем, используя свой циркуль, поставьте его конец на одном из концов гипотенузы и рисуйте дугу, чтобы сформировать прямой угол с гипотенузой. Повторите этот шаг, чтобы определить второй конец основания треугольника.
3. Постройте второй катет, используя гипотенузу и другой катет. Снова начните с рисования отрезка, который представляет гипотенузу, и отметьте его концы. Затем, используя циркуль, поставьте его конец на одном из концов гипотенузы и рисуйте дугу, чтобы сформировать прямой угол с гипотенузой. Повторите этот шаг, чтобы определить второй конец второго катета.
4. Убедитесь, что основание и отрезок-катеты встречаются в одной точке, чтобы создать прямой угол между ними. Если это не так, проверьте ваши измерения и повторите шаги, если необходимо.
5. Проверьте свою работу, убедившись, что длины сторон треугольника соответствуют вашим исходным данным. Помните, что для прямоугольного треугольника выполненная теорема Пифагора, которая гласит: a^2 + b^2 = c^2, где a и b - это катеты, а c - гипотенуза.

Построение прямоугольного треугольника может быть использовано для решения различных задач в геометрии и на практике. Например, его можно использовать для расчета векторов или для определения расстояния между двумя точками в пространстве.

Использование простых геометрических принципов и этого подробного руководства позволит вам легко и точно построить прямоугольный треугольник.

Требуемые инструменты и материалы

Для построения прямоугольного треугольника по гипотенузе и катету вам понадобятся следующие инструменты и материалы:

• Линейка или измерительная лента.
• Карандаш.
• Угольник или геодезическая транспортира.
• Бумага или лист для рисования.

Убедитесь, что ваши инструменты находятся в исправном состоянии и соответствуют требованиям точности для строительных работ. Также убедитесь, что у вас есть достаточно света и пространства для работы.

Выбор гипотенузы и катета

При конструировании прямоугольного треугольника по гипотенузе и катету необходимо правильно выбрать значения этих сторон. Гипотенузой называется наибольшая сторона треугольника, противоположная прямому углу. Катетами называются две меньшие стороны, из которых одна смежна с прямым углом.

Хорошим подходом при выборе гипотенузы и катета является определение требований конкретной задачи или конструкции, в которую будет встроен треугольник. Например, если вам нужен перпендикуляр к определенному отрезку, может быть удобно выбрать этот отрезок в качестве гипотенузы, а его одну из концевых точек в качестве одного из катетов. Таким образом, вы будете строить треугольник исходя из требований вашей задачи или конструкции.

Важно также учитывать, что прямоугольный треугольник обладает определенными свойствами, например, теоремой Пифагора, которую можно использовать для проверки правильности выбранных значений. Необходимо учитывать эти свойства при выборе гипотенузы и катета, чтобы далее можно было уверенно выполнять дальнейшие вычисления и конструирование треугольника.

Подготовка к построению

Перед началом построения прямоугольного треугольника по гипотенузе и катету необходимо выполнить несколько подготовительных шагов:

1. Выберите место, где будете проводить построение. Убедитесь, что на выбранной поверхности можно без проблем проводить линии и замеры.
2. Приготовьте инструменты, необходимые для построения. Вам понадобится линейка, карандаш, циркуль и прозрачная пластиковая линейка со скользящей блокировкой для измерений.
3. Очистите выбранную поверхность от лишней пыли и мусора. Это поможет вам проводить линии и измерения точнее.

После выполнения этих шагов вы готовы приступить к построению прямоугольного треугольника.

Построение треугольника

Для построения прямоугольного треугольника по заданным гипотенузе и катету необходимо выполнить следующие шаги:

1. Начните со схематического изображения треугольника на листе бумаги или в графическом редакторе.
2. Обозначьте гипотенузу и катеты на схеме.
3. Измерьте длину гипотенузы и катета с помощью линейки или другого измерительного инструмента.
4. На листе бумаги или в графическом редакторе отметьте начало гипотенузы и катета.
5. Соедините отмеченные точки, чтобы получить прямые линии, соответствующие гипотенузе и катету треугольника.
6. Проверьте, что гипотенуза и катеты образуют прямой угол.
7. Если необходимо, проведите дополнительные измерения или корректировки для точного построения треугольника.

Проверка прямоугольности треугольника

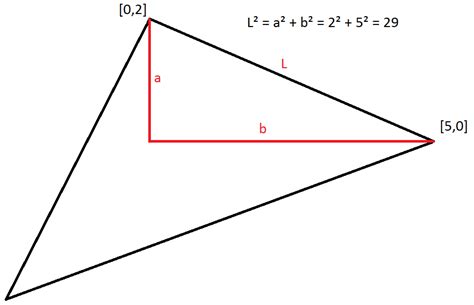
Для проверки прямоугольности треугольника с заданными гипотенузой и катетом нужно выполнить следующие шаги:

1. Возвести катет в квадрат и получить его квадрат.
2. Возвести гипотенузу в квадрат и получить ее квадрат.
3. Сложить квадраты катета и гипотенузы.
4. Проверить, равны ли полученная сумма и квадрат гипотенузы.

Если сумма квадратов катета и гипотенузы равна квадрату гипотенузы, то треугольник является прямоугольным.

Пример:

Пусть катет треугольника равен 3, а гипотенуза равна 5. Тогда:

Квадрат катета: 3² = 9

Квадрат гипотенузы: 5² = 25

Сумма квадратов катета и гипотенузы: 9 + 25 = 34

Квадрат гипотенузы: 5² = 25

Поскольку сумма квадратов катета и гипотенузы (34) не равна квадрату гипотенузы (25), треугольник не является прямоугольным.