В геометрии равнобедренным треугольником называется треугольник, у которого две стороны равны между собой, а третья сторона называется основанием. Особенностью равнобедренного треугольника является то, что углы, прилежащие к основанию, также равны. Свойство равенства этих углов называется свойством внутренних углов.
На практике, часто возникает необходимость создания равнобедренного треугольника по общему основанию. Для этого существуют различные методы и конструкции. Одной из самых простых и распространенных является конструкция на основе угла, смежного с основанием.
Для конструирования равнобедренного треугольника по общему основанию необходимо сначала построить данное основание, а затем поставить на нем определенный угол, смежный с основанием. Для этих операций можно использовать различные инструменты и методы, такие как линейка, угольник, циркуль и компас.
Что такое равнобедренный треугольник?
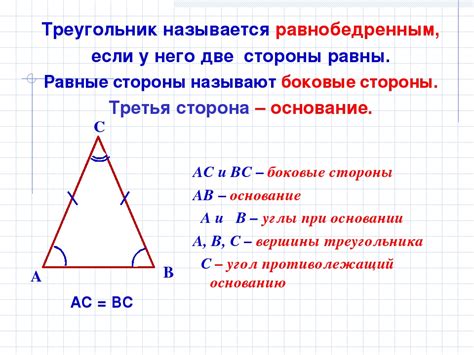
Равнобедренные треугольники можно построить, зная длину основания и одного из углов. Также можно построить равнобедренный треугольник, зная длины двух равных сторон и угол между ними. Наиболее простая конструкция равнобедренного треугольника состоит в построении его высоты, которая является биссектрисой основания и делит его на две равные части.
Равнобедренные треугольники имеют несколько интересных свойств. Например, углы при основании равнобедренного треугольника также являются равными. Также, высота треугольника, проведенная из вершины противолежащей основанию, является медианой и перпендикулярна основанию. Эти особенности делают равнобедренные треугольники удобными для решения различных задач в геометрии и физике.
Равнобедренные треугольники часто встречаются в естественных и геометрических формах. Например, пирамида, у которой основание является равнобедренным треугольником, имеет особую структуру и применяется в архитектуре и строительстве. Также, равнобедренные треугольники играют важную роль в тригонометрии при вычислении тригонометрических функций и решении различных задач, связанных с углами и сторонами треугольника.
Основные характеристики равнобедренных треугольников
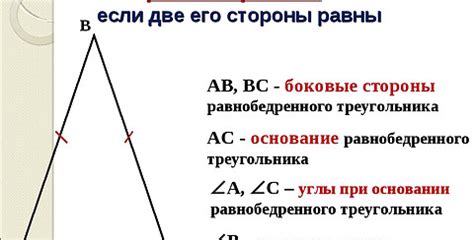
- У равнобедренного треугольника две равные стороны, называемые равными боковыми сторонами.
- Основание равнобедренного треугольника – это третья сторона, которая отличается от боковых сторон.
- Вершины равнобедренного треугольника, расположенные напротив равных боковых сторон, называются вершинами угла, а углы при этих вершинах – вершинными углами. Вершинный угол, расположенный напротив основания, называется основным углом.
- Основной угол равнобедренного треугольника всегда равен.
- Сумма углов равнобедренного треугольника всегда равна 180 градусов.
- Один из способов определить равнобедренность треугольника – это равенство углов при основании.
- Равнобедренные треугольники могут быть разносторонние или равносторонние.
Изучение равнобедренных треугольников очень важно, так как они широко применяются в геометрии и других областях науки и техники.
Как построить равнобедренный треугольник по общему основанию?

Шаг 1: Нарисуйте отрезок AB, который будет служить основанием треугольника.
Шаг 2: На середине отрезка AB поставьте точку C. Эта точка будет служить вершиной треугольника.
Шаг 3: Прокладывая от точек A и B равные отрезки, постройте два угла равные друг другу. Это можно сделать с помощью геометрической конструкции или с использованием транспортира.
Шаг 4: Проведите две прямые линии от вершины C до пересечения с продолжением отрезков AB. Обозначьте точки пересечения прямых линий с AB как D и E.
Шаг 5: Полученный треугольник CDE будет равнобедренным треугольником с общим основанием AB.
Таким образом, используя описанную конструкцию, вы можете построить равнобедренный треугольник по общему основанию. Убедитесь, что все измерения и углы согласуются в процессе построения.
| Шаг | Описание | Иллюстрация |
|---|---|---|
| Шаг 1 | Нарисуйте отрезок AB, который будет служить основанием треугольника. |  |
| Шаг 2 | На середине отрезка AB поставьте точку C. |  |
| Шаг 3 | Прокладывая от точек A и B равные отрезки, постройте два угла равные друг другу. |  |
| Шаг 4 | Проведите две прямые линии от вершины C до пересечения с продолжением отрезков AB. Обозначьте точки пересечения прямых линий с AB как D и E. |  |
| Шаг 5 | Полученный треугольник CDE будет равнобедренным треугольником с общим основанием AB. |  |
Примеры построения равнобедренных треугольников
Существует несколько способов построения равнобедренного треугольника по общему основанию:
1. Метод через равнобедренный треугольник:
| Шаги построения | Пример |
|---|---|
| 1. Провести отрезок AB, который будет являться основанием треугольника. |  |
| 2. Раскладываем циркуль из точки A и B, проводим окружности с одинаковым радиусом. |  |
| 3. Точки пересечения окружностей - вершины треугольника. |  |
2. Метод через равнобедренный треугольник и точку на продолжении основания:
| Шаги построения | Пример |
|---|---|
| 1. Провести отрезок AB, который будет являться основанием треугольника. |  |
| 2. Проложить прямую через точку B, продолжая основание треугольника. |  |
| 3. Раскладываем циркуль из точки A, проводим окружность с радиусом, равным отрезку AB. |  |
| 4. Точки пересечения окружности и прямой - вершины треугольника. |  |
Это лишь некоторые примеры построения равнобедренных треугольников по общему основанию. В зависимости от условий задачи могут использоваться и другие методы.
Как вычислить площадь равнобедренного треугольника?
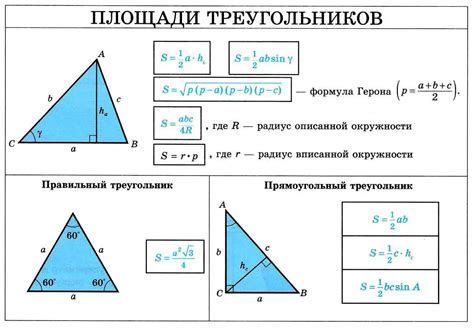
Для вычисления площади равнобедренного треугольника необходимо знать длину его основания и высоту, опущенную на это основание. Равнобедренный треугольник имеет две равные стороны и два равных угла, которые расположены напротив этих сторон.
Если известно основание треугольника и длина высоты, можно воспользоваться формулой для вычисления площади равнобедренного треугольника:
| Формула: | Площадь = (Основание * Высота) / 2 |
Например, если основание равнобедренного треугольника равно 10 сантиметров, а высота равна 8 сантиметрам, то площадь равнобедренного треугольника будет:
| Площадь = (10 * 8) / 2 = 40 сантиметров квадратных |
Таким образом, площадь равнобедренного треугольника с указанными значениями будет равна 40 сантиметров квадратных.
Важно помнить, что для вычисления площади равнобедренного треугольника необходимо знать длину основания и длину высоты, опущенной на это основание. Если одно из этих значений неизвестно, то площадь невозможно вычислить.
Особенности равнобедренных треугольников
| Особенность | Объяснение |
|---|---|
| Стороны | В равнобедренном треугольнике две стороны равны друг другу, пока третья сторона может быть разной длины. |
| Углы у основания | В равнобедренном треугольнике углы при основании равны друг другу. |
| Углы при основании | Углы при основании равнобедренного треугольника равны между собой. |
| Высота | Высота равнобедренного треугольника, опущенная на основание, является биссектрисой. |
Равнобедренные треугольники встречаются в различных геометрических задачах и конструкциях. Их свойства и особенности позволяют упростить решение задач и выполнить точную конструкцию фигур. Поэтому знание особенностей равнобедренных треугольников является важным в геометрии.
Применение равнобедренных треугольников в геометрии и архитектуре
Еще одно применение равнобедренных треугольников заключается в измерении высоты или ширины объектов в архитектуре. Например, при проектировании зданий, можно использовать равнобедренные треугольники для определения высоты, а также для расчетов углов и площадей поверхностей.
В архитектуре равнобедренные треугольники также используются для создания прочных и устойчивых конструкций. Благодаря их особенностям, равнобедренные треугольники могут служить опорными точками для строительных элементов, обеспечивая им дополнительную стабильность.
Также равнобедренные треугольники используются при раскладке каркасов зданий или мостов, что позволяет добиться более равномерного распределения нагрузки и увеличить прочность конструкции.
Таким образом, равнобедренные треугольники являются неотъемлемой частью геометрии и архитектуры. Они позволяют более эффективно решать задачи, связанные с измерением и конструированием, а также способствуют созданию прочных и устойчивых строительных конструкций.