Начертательная геометрия - одна из фундаментальных дисциплин, которая изучает пространственные фигуры и их свойства. В этой статье мы рассмотрим основные шаги, необходимые для построения треугольника, используя инструменты и знания начертательной геометрии.
Первым шагом в конструкции треугольника является выбор основания. Основанием треугольника может служить отрезок, линия или даже поверхность. После выбора основания, необходимо определить длину его сторон. Для этого можно использовать геометрический компас и линейку.
Далее, нужно построить вершины треугольника. Вершины могут быть расположены на концах сторон, на серединах сторон или на пересечении сторон с другими линиями. При построении треугольника необходимо учесть, что сумма длин любых двух сторон треугольника должна быть больше третьей стороны.
После построения вершин треугольника, можно провести его стороны. Для этого следует использовать прямую линию или линейку. Стороны треугольника должны быть прямыми отрезками, соединяющими соответствующие вершины. Убедитесь, что стороны не пересекаются и не пересекают основание треугольника.
В результате правильно построенного треугольника, его стороны будут образовывать три угла. Углы треугольника могут быть равными или неравными. Для измерения углов можно использовать геометрический угольник или универсальный угольник.
Определение треугольника
Сторона треугольника - это отрезок, соединяющий две вершины треугольника. Угол треугольника - это область плоскости, ограниченная двумя сторонами треугольника.
Треугольники могут быть классифицированы по различным характеристикам, таким как длины сторон и величины углов.
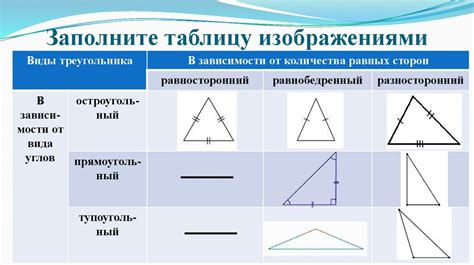
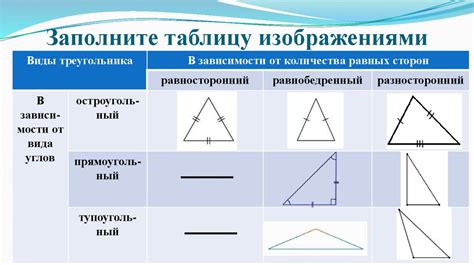
В зависимости от длин сторон, треугольники могут быть:
- Равносторонними - треугольник, у которого все стороны равны.
- Равнобедренными - треугольник, у которого две стороны равны.
- Разносторонними - треугольник, у которого все стороны различны.
В зависимости от величин углов, треугольники могут быть:
- Остроугольными - треугольник, у которого все углы меньше 90 градусов.
- Тупоугольными - треугольник, у которого один угол больше 90 градусов.
- Прямоугольными - треугольник, у которого один угол равен 90 градусов.
Сумма углов треугольника всегда равна 180 градусов. Это свойство треугольников называется теоремой о сумме углов треугольника.
Что такое треугольник и зачем нужно его изучать?
Изучение треугольника позволяет узнать основные свойства и закономерности этой фигуры. Например, треугольник может быть различных типов в зависимости от длин сторон и величин углов. Изучение этих типов позволяет анализировать и классифицировать различные геометрические объекты. Кроме того, треугольник является основой для изучения более сложных фигур, таких как прямоугольник, квадрат, параллелограмм и т.д.
Изучение треугольника также важно для понимания многих практических сфер, таких как архитектура, строительство и инженерное дело. Многие конструкции и расчеты требуют знания свойств треугольников. Например, для построения прочной конструкции необходимо правильно рассчитать углы и длины сторон треугольника.
Кроме того, изучение треугольника способствует развитию логического и аналитического мышления. Решение геометрических задач требует умения анализировать информацию, находить закономерности и применять математические методы для решения задач. Таким образом, изучение треугольника помогает развить навыки логического мышления и абстрактного мышления, которые могут быть полезными во многих сферах жизни.
Таким образом, изучение треугольника является необходимой и важной задачей в начертательной геометрии. Знание свойств и закономерностей треугольника позволяет развивать логическое мышление, аналитические навыки и применять их в практических задачах. Идеальное владение треугольником является основой для изучения и понимания более сложных геометрических фигур.
Свойства треугольника
У треугольника есть несколько важных свойств:
- Сумма углов треугольника: Внутренние углы треугольника в сумме дают 180 градусов. Это означает, что сумма трех углов треугольника всегда равна 180°.
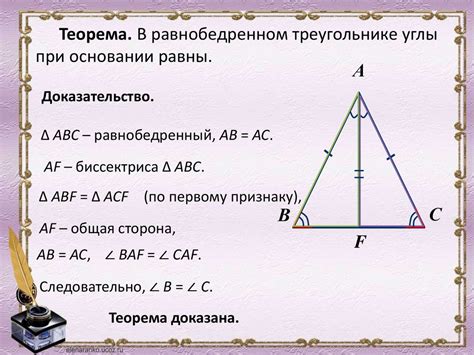
- Типы треугольников: В зависимости от своих свойств треугольники могут быть различных типов. Например, равносторонний треугольник имеет три равные стороны и три равных угла. Равнобедренный треугольник имеет две равные стороны и два равных угла. Прямоугольный треугольник имеет прямой угол, то есть угол, равный 90 градусов.
- Сумма длин двух сторон больше третьей: В любом треугольнике сумма длин двух сторон всегда больше длины третьей стороны. Это называется неравенством треугольника.
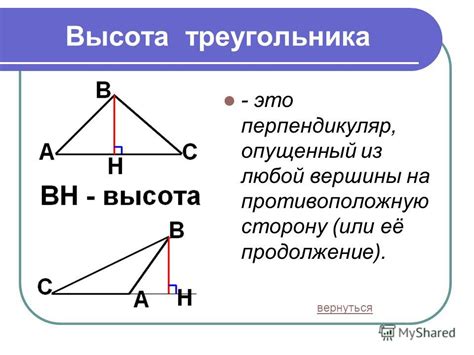
- Высоты треугольника: Высоты треугольника – это перпендикуляры, опущенные из вершин треугольника на противоположные стороны. Высоты могут быть внутренними (опущены внутрь треугольника) или внешними (опущены за пределы треугольника).
Понимание этих свойств поможет вам лучше понять треугольники и использовать их в решении геометрических задач и задач построения.
Какие свойства имеет треугольник и как их использовать при его изучении?
Основные свойства треугольника:
| Стороны | Каждая сторона треугольника – это отрезок, соединяющий две вершины. Сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Это неравенство называется неравенством треугольника и является одним из ключевых свойств треугольника. |
| Углы | У треугольника есть три угла, образованных сторонами. Сумма всех углов треугольника всегда равна 180°. Это свойство называется суммой углов треугольника и также является важным при изучении треугольников. |
| Высоты и медианы | Высота треугольника – это отрезок, перпендикулярный одной из сторон треугольника и проходящий через противоположную вершину. Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Высоты и медианы имеют важное значение при решении различных задач и нахождении различных характеристик треугольника. |
| Площадь | Площадь треугольника – это мера его поверхности. Площадь треугольника можно найти, зная длины его сторон и высоту, проведенную к одной из сторон. Формула для нахождения площади треугольника зависит от известных данных и может быть разной для различных видов треугольников. |
| Теорема Пифагора | Теорема Пифагора – это одна из самых известных теорем в математике, которая гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Эта теорема широко используется при решении задач, связанных с треугольниками. |
Используя эти свойства и знания о треугольниках, можно решать различные задачи, связанные с их изучением, нахождением характеристик и применением в практических ситуациях.
Как построить треугольник
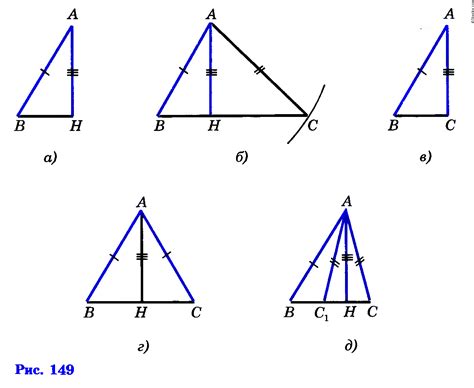
1. Определите длины сторон треугольника. Если известны только углы треугольника, воспользуйтесь тригонометрическими соотношениями для определения соответствующих сторон.
2. Начертите на листе бумаги отрезки, соответствующие длинам сторон треугольника в масштабе. Обозначьте их буквами A, B и C.
3. Найдите пересечение отрезков AB и BC. Обозначьте полученную точку буквой D.
4. Соедините точки A и B отрезком, обозначьте его буквой AB. Соедините точки B и C отрезком, обозначьте его буквой BC. Соедините точки C и D отрезком, обозначьте его буквой CD.
5. Убедитесь, что отрезки AB, BC и CD не пересекаются внутри фигуры. Если пересекаются, проверьте правильность выполнения предыдущих шагов.
6. Проверьте, что отрезки AB, BC и CD образуют замкнутую фигуру без самопересечений. Если есть самопересечения, убедитесь, что все шаги выполнены правильно.
7. Треугольник построен. Обозначьте его буквами ABC.
При выполнении этих шагов соблюдайте точность и аккуратность. Только правильно построенный треугольник даст корректные результаты при решении геометрических задач!
Шаги и инструкции для правильного построения треугольника
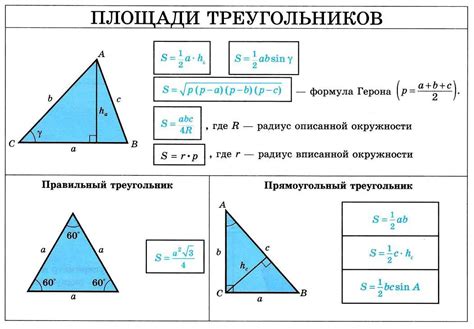
- Нарисуйте основание треугольника, которое будет являться отрезком прямой линии.
- Укажите середину основания треугольника и проведите от нее перпендикуляр, с помощью циркуля и линейки, вверх от основания.
- С помощью циркуля и линейки, измерьте расстояние от середины основания до ее конца и отметьте эту точку на перпендикуляре.
- Соедините точку на перпендикуляре с концами основания треугольника, чтобы получить две наклонные стороны треугольника.
- Убедитесь, что все стороны треугольника имеют одинаковую длину, измерьте длины отрезков с помощью линейки.
- Проведите линии, соединяющие концы наклонных сторон треугольника, чтобы закрыть его и создать правильный треугольник.
Проделав все эти шаги, вы получите правильный треугольник, у которого все стороны равны и все углы равны 60 градусам. Используя эти инструкции, вы сможете легко нарисовать любой правильный треугольник.