Осевое сечение является одной из важных концепций в геометрии. Довольно часто возникают ситуации, когда необходимо найти осевое сечение для конуса. Знание методов и приемов для решения таких задач является крайне полезным и может пригодиться в различных областях, включая строительство, машиностроение и архитектуру.
Осевое сечение конуса представляет собой плоскость, которая пересекает конус вдоль его оси. Плоскость проходит через вершину конуса и разделяет его на две симметричные части. При нахождении осевого сечения необходимо определить его форму и размеры. Для этого можно использовать несколько методов и алгоритмов.
Один из простых способов найти осевое сечение конуса - использовать геометрические свойства фигуры. Если известны высота и радиус основания конуса, можно построить плоскость, проходящую через вершину и центр основания. Такая плоскость будет служить осевым сечением, которое разделит конус на две равные части.
Определение осевого сечения
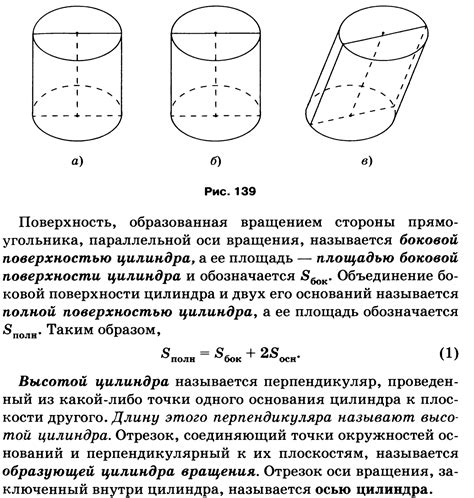
В осевом сечении будут видны основание конуса и его ось. Однако, все элементы, находящиеся на расстоянии от оси большем, чем радиус основания, будут невидимы в этом сечении.
Осевое сечение имеет форму эллипса тогда и только тогда, когда плоскость сечения проходит через центр основания конуса. В противном случае, оно будет касательным параболе или овалу.
Осевые сечения важны при решении задач, связанных с конусами. Они помогают определить форму и размеры сечений, а также найти интересующие нас параметры. Зная форму осевого сечения, мы можем рассчитать площадь, периметр, высоту и другие характеристики фигуры, которую оно образует.
Конус, его параметры и формула объема
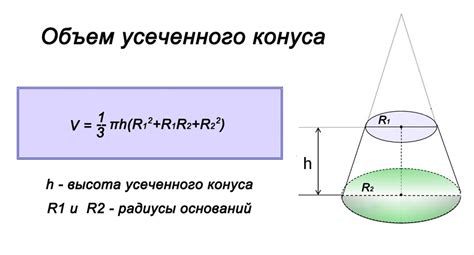
Основание конуса - это закрытая плоская фигура, которая может быть кругом, эллипсом или многоугольником.
Ребро конуса - это отрезок, соединяющий вершину с точками основания.
Высота конуса - это расстояние между вершиной и плоскостью основания.
Объем конуса можно вычислить по формуле:
V = (1/3) * π * r^2 * h,
где V - объем конуса, π - число пи (приближенно равно 3,14), r - радиус основания, h - высота конуса.
Зная радиус основания и высоту конуса, можно вычислить его объем.
Особенности осевого сечения конуса
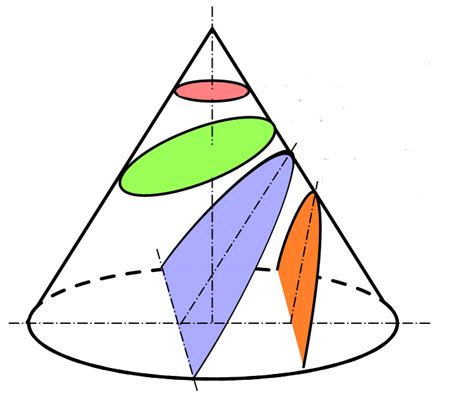
Осевое сечение конуса представляет собой плоскую фигуру, полученную путем пересечения плоскости с осью конуса. Осевое сечение конуса имеет ряд особенностей, которые важно учитывать при изучении данного геометрического объекта.
Одна из основных особенностей осевого сечения конуса заключается в том, что оно всегда является эллипсом. Форма эллипса зависит от положения плоскости, которая проходит через ось конуса. Если плоскость параллельна основанию конуса, то осевое сечение будет кругом. А если плоскость пересекает конус под углом, то получится эллипс с различными полуосями.
Еще одной важной особенностью осевого сечения конуса является его центр. Центр эллипса осевого сечения находится на пересечении плоскости с осью конуса. Это означает, что осевое сечение всегда будет симметричным относительно центра.
Также стоит отметить, что осевое сечение конуса может быть эллипсом или окружностью в зависимости от типа конуса. Например, у прямого конуса все осевые сечения будут кругами. А у наклонного конуса осевые сечения будут эллипсами с различными полуосями.
Важно понимать, что осевое сечение конуса играет важную роль в геометрии и имеет множество применений в различных областях науки и техники. Изучая особенности осевого сечения, можно получить полное представление о форме и свойствах конуса.
| Тип конуса | Особенности осевого сечения |
|---|---|
| Прямой конус | Все осевые сечения являются кругами |
| Наклонный конус | Осевые сечения являются эллипсами с различными полуосями |
Методы определения осевого сечения
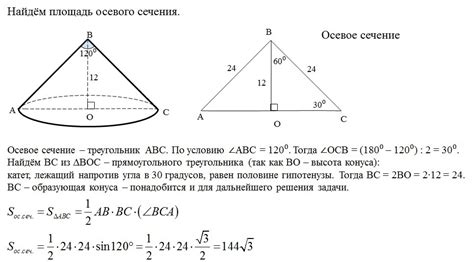
| Метод | Описание |
| Метод пересечения | Данный метод заключается в пересечении плоскости, проходящей через вершину и ось конуса, с плоскостью, которую необходимо определить как осевое сечение. Построив сечение, можно определить его форму и размеры. |
| Метод параметризации | При использовании этого метода осевое сечение определяется с помощью параметрического описания, задаваемого уравнением плоскости. Это позволяет более точно определить осевое сечение и рассчитать его характеристики. |
| Метод графической интерполяции | Этот метод основан на графической интерполяции геометрических данных конуса. Используя известные размеры и форму конуса, можно примерно определить его осевое сечение, нарисовав его на графике или чертеже. |
Каждый из этих методов имеет свои преимущества и ограничения, поэтому их выбор зависит от конкретной задачи и доступных данных о конусе. Важно использовать правильный метод для достижения точных результатов при определении осевого сечения конуса.
Практическое применение осевых сечений конуса
Осевые сечения конуса имеют широкое практическое применение в различных областях, включая инженерию, архитектуру и геометрию.
- Инженерия: Осевые сечения конуса используются для проектирования и изготовления различных инженерных конструкций, таких как вентиляционные трубы, обратные конусы для ракет и многое другое. Осевые сечения помогают инженерам определить форму и размеры каждого сечения для достижения желаемых результатов.
- Архитектура: При проектировании архитектурных сооружений, осевые сечения конуса играют важную роль в определении формы и размеров различных элементов, таких как колонны, столбы, купола и крыши. Они позволяют архитекторам лучше визуализировать и представить конструкцию в трехмерном пространстве.
- Геометрия: В геометрии, осевые сечения конуса используются для изучения различных свойств конусов и их взаимосвязи с другими геометрическими фигурами. Они помогают ученым и студентам лучше понять геометрические принципы и применить их в реальной жизни.
Все эти примеры демонстрируют практическое значение осевых сечений конуса. Они являются важным инструментом для решения различных задач в разных областях и способствуют более точному и эффективному проектированию и изготовлению.