Перевод дроби в десятичную дробь – одна из основных задач, с которой сталкиваются все, кто изучает математику. Этот процесс может вызывать затруднения, особенно у начинающих, но на самом деле, он не так сложен, как кажется. В этой статье мы рассмотрим несколько простых шагов, которые помогут вам правильно перевести дробь в десятичную дробь.
Прежде чем начать перевод, важно понять основные термины и определения. Дробь состоит из двух чисел: числителя и знаменателя. Числитель – это верхняя часть дроби, которая показывает, сколько долей целого имеется. Знаменатель – это нижняя часть дроби, которая показывает, на сколько долей целое разделено. Например, в дроби 3/4, числитель равен 3, а знаменатель равен 4.
Перевод дроби в десятичную дробь осуществляется путем деления числителя на знаменатель. При этом важно учесть, что некоторые дроби могут быть циклическими, то есть иметь бесконечное количество десятичных знаков.
Определение десятичной дроби
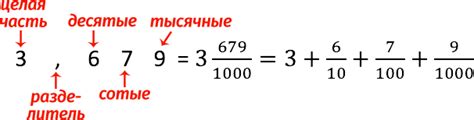
Десятичная дробь может быть переведена из обычной дроби путем деления числителя на знаменатель. Результатом деления будет бесконечная или конечная десятичная дробь. Если дробь является периодической, то в десятичной записи одна или несколько цифр повторяются бесконечное количество раз.
Например, дробь 1/3 в десятичной записи будет иметь вид 0.3333..., где тройка повторяется бесконечное количество раз. Дробь 2/5 в десятичной записи будет 0.4.
Десятичные дроби важны во многих областях, включая финансы, науку и инженерию. Они позволяют точно измерять дробные значения и использовать их для выполнения различных математических операций.
Понятие десятичной дроби

Десятичная дробь может быть конечной или бесконечной. В конечной десятичной дроби после запятой или точки идет определенное количество знаков, в то время как в бесконечной десятичной дроби последовательность знаков повторяется бесконечно.
Для перевода обыкновенной дроби в десятичную дробь необходимо разделить числитель на знаменатель и записать результат в виде десятичной дроби. Если полученная десятичная дробь является конечной, то перевод считается завершенным. В противном случае, если десятичная дробь повторяется или образует бесконечную последовательность, необходимо найти период повторяемости и обозначить его специальным символом над повторяющейся последовательностью.
| Термин | Описание |
|---|---|
| Десятичная дробь | Десятичное представление рационального числа, состоящее из десятичной части и десятичной части. |
| Десятичная часть | Число перед запятой в десятичной дроби. |
| Дробная часть | Число после запятой или точки в десятичной дроби. |
| Конечная десятичная дробь | Десятичная дробь с определенным количеством знаков после запятой или точки. |
| Бесконечная десятичная дробь | Десятичная дробь, в которой последовательность знаков повторяется бесконечно. |
Примеры десятичных дробей

Для лучшего понимания процесса перевода обыкновенной дроби в десятичную дробь рассмотрим несколько примеров:
| Обыкновенная дробь | Десятичная дробь |
|---|---|
| 1/2 | 0.5 |
| 3/4 | 0.75 |
| 2/5 | 0.4 |
| 5/8 | 0.625 |
Как видно из примеров, десятичная дробь представляет собой число с десятичной точкой, где числитель обыкновенной дроби становится цифрами до точки, а знаменатель становится числом после точки. Для определения длины периода в периодической десятичной дроби используется метод деления, который позволяет найти повторяющуюся последовательность цифр.
Используя эти примеры, можно легко освоить навык перевода обыкновенной дроби в десятичную форму и улучшить понимание математических операций с дробями.
Как получить десятичную дробь из обыкновенной

Существует несколько способов получения десятичной дроби из обыкновенной. Один из самых распространенных способов - деление числителя на знаменатель. Этот метод подходит для обыкновенных дробей, у которых знаменатель не является десятичной дробью или содержит только конечное число десятичных разрядов.
Для начала, делим числитель на знаменатель. Затем продолжаем деление, приписывая нули к остатку и деля на знаменатель до тех пор, пока не получим требуемое количество десятичных разрядов или пока не закончится остаток.
Если остаток в какой-то момент начинает повторяться, значит, десятичная дробь является периодической. В этом случае, повторение остатка после запятой обычно обозначается фигурной скобкой над повторяющейся частью.
Например, пусть у нас есть дробь 3/4. Для перевода ее в десятичную дробь, мы делим 3 на 4:
- 3 / 4 = 0.75
Таким образом, десятичная дробь, эквивалентная 3/4, равна 0.75.
Однако, не все обыкновенные дроби можно точно представить в виде десятичной дроби. Например, дробь 1/3 не имеет конечного представления в десятичной системе. При делении 1 на 3 мы получим бесконечную последовательность троек после запятой: 0.33333333...
Поэтому, при переводе дробей в десятичные дроби, необходимо учитывать, что некоторые дроби могут иметь периодическое представление или быть бесконечными.
Шаг 1: Определение числа после запятой

Перевод дроби в десятичную дробь начинается с определения числа десятичных разрядов, которые понадобятся для точного представления. Число после запятой определяет, сколько цифр будет находиться после запятой в десятичном представлении.
Например, если дробь имеет знаменатель, кратный степени 10 (например, 10, 100, 1000 и т. д.), то десятичная дробь будет иметь ограниченное число десятичных разрядов, равное числу нулей в знаменателе. Например, дробь 2/10 будет иметь один десятичный разряд, а дробь 3/100 будет иметь два десятичных разряда.
Если знаменатель не является кратным степени 10, то число десятичных разрядов будет определяться размером знаменателя. Чем больше знаменатель, тем больше десятичных разрядов будет требоваться для точного представления десятичной дроби.
Определение числа после запятой очень важно для правильного перевода дроби в десятичную дробь. Неправильное определение может привести к округлению или обрезанию десятичных разрядов и, следовательно, к неточному представлению дроби.