Двоичная система счисления является основой для работы компьютеров и программирования. Понимание того, как конвертировать число в двоичную систему, может быть очень полезным навыком для разработчиков и всех, кто работает с компьютерами.
В этом подробном руководстве мы рассмотрим процесс конвертации чисел из десятичной системы счисления в двоичную. Вы узнаете основные правила и шаги для выполнения этой операции, а также получите несколько примеров для лучшего понимания.
Прежде чем начать, важно понимать, что двоичная система счисления основана на использовании только двух символов: 0 и 1. Числа записываются справа налево, где каждая цифра представляет степень числа 2. Например, число 1010 в двоичной системе эквивалентно числу 10 в десятичной системе.
Теперь перейдем непосредственно к процессу конвертации. Загляните в наше подробное руководство, чтобы полностью освоить этот навык и с легкостью выполнять конвертацию чисел в двоичную систему.
Что такое двоичная система и зачем она нужна?

Зачем нам нужна двоичная система? Перевод чисел в двоичную систему позволяет нам эффективно хранить и обрабатывать данные. В отличие от десятичной системы, которая использует десять цифр от 0 до 9, двоичная система является более простой и надежной, так как она основывается на двух основных состояниях. Кроме того, двоичная система легко сопоставляется с электронными сигналами, что делает ее идеальной для работы с электронными устройствами.
Преобразование чисел в двоичную систему также позволяет нам легко выполнить различные операции, такие как сложение, вычитание, умножение и деление. Это особенно важно в программировании и компьютерных науках, где двоичная система является основой для работы с битами и байтами.
Таким образом, двоичная система играет важную роль в области информатики и электроники, обеспечивая простой и эффективный способ представления и обработки данных. Понимание двоичной системы помогает нам лучше понять работу компьютеров и сделать наши программы и устройства более эффективными.
Преимущества использования двоичной системы

Преимущества использования двоичной системы включают:
Простота и надежность: В отличие от десятичной системы, которая требует использования десяти различных цифр, двоичная система использует всего две цифры - 0 и 1. Это делает ее намного проще для понимания и работы с ней. Кроме того, двоичная система более устойчива к ошибкам, поскольку ее составляющие элементы намного проще и надежнее в использовании.
Универсальность: Двоичная система является универсальной системой численности, которая применима в различных областях науки и техники. Она используется в компьютерах, электронике, цифровой связи, технологии программирования и многих других областях. Благодаря своей универсальности, двоичная система позволяет эффективно передавать, обрабатывать и хранить информацию, что особенно важно в современном информационном мире.
Простота арифметических операций: В двоичной системе арифметические операции, такие как сложение, вычитание, умножение и деление, намного проще и эффективнее, чем в десятичной системе. В двоичной системе все арифметические операции сводятся к простым правилам, которые легко применять в компьютерных и электронных устройствах. Это позволяет обеспечить более эффективное и быстрое выполнение арифметических операций.
Легкость представления и хранения данных: В двоичной системе числа могут быть представлены и хранятся с использованием меньшего количества битов, чем в десятичной системе. Это делает представление и хранение данных более экономичным и эффективным. Кроме того, двоичная система позволяет компактно представлять и обрабатывать большие объемы информации, что особенно полезно в области компьютеров и цифровых устройств.
Все эти преимущества позволяют сделать двоичную систему основой современных технологий и средств коммуникации. Она является основой для работы компьютеров, цифровой техники и различных программных систем. Поэтому знание и понимание двоичной системы является важным элементом образования в области информационных технологий и компьютерных наук.
Подготовка

Также, убедитесь, что вы знакомы с понятиями разрядов и позиционных значений. В двоичной системе каждая цифра занимает определенный разряд и имеет свое позиционное значение. Например, в числе 1011 первая цифра имеет позиционное значение 1, вторая - 2, третья - 4, а четвертая - 8.
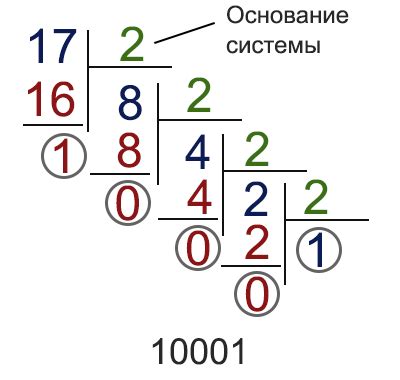
Кроме того, имеет смысл ознакомиться с основными правилами конвертирования чисел в двоичную систему. Одно из таких правил - деление числа на 2 и запись остатка внизу, повторяя процесс до тех пор, пока не получится нулевое значение. Например, для числа 10 процесс выглядит следующим образом: 10/2 = 5 и остаток 0, 5/2 = 2 и остаток 1, 2/2 = 1 и остаток 0, 1/2 = 0 и остаток 1. Остатки в обратном порядке составляют двоичное представление числа - 1010.
Список материалов, необходимых для конвертации числа в двоичную систему
Для успешной конвертации числа в двоичную систему вам понадобятся следующие материалы:
- Бумага и ручка для записи промежуточных результатов.
- Калькулятор для выполнения арифметических операций.
- Книга или статья, содержащая методику конвертации числа в двоичную систему.
- Система счисления и правила перевода чисел в двоичную форму.
- Тренировочные примеры для отработки навыков конвертации.
Не забывайте, что для эффективного изучения процесса конвертации чисел в двоичную систему, нужно обладать базовыми знаниями арифметики и привыкнуть к ручной работе с числами. Удачной работы!
Шаги конвертации
- Разделите исходное число на 2.
- Запишите остаток от деления (0 или 1) в начало нового числа, это будет самый младший бит.
- Если результат деления равен 0, прекратите процесс конвертации.
- В противном случае, повторите шаги 1-3 для частного.
- В конце получите двоичное число, записав все остатки в обратном порядке.
Шаг 1: Перевод числа из десятичной системы счисления в двоичную

- Начните с самого правого (младшего) разряда и работайте в сторону самого левого (старшего) разряда.
- Разделите число на 2.
- Запишите остаток от деления на 2.
- Продолжайте делить полученное целочисленное значение на 2 и записывать остатки до тех пор, пока не получите 0.
- Запишите полученные остатки в обратном порядке - это и будет двоичное представление числа.
Вот пример:
Дано число 42.
Начнем с самого правого разряда и поделим число на 2:
- 42 ÷ 2 = 21 остаток 0
Далее, поделим полученное целочисленное значение на 2:
- 21 ÷ 2 = 10 остаток 1
Продолжим делить:
- 10 ÷ 2 = 5 остаток 0
- 5 ÷ 2 = 2 остаток 1
- 2 ÷ 2 = 1 остаток 0
- 1 ÷ 2 = 0 остаток 1
Запишем полученные остатки в обратном порядке: 101010.
Таким образом, число 42 в двоичной системе равно 101010.
Шаг 2: Визуализация двоичного числа

После того, как мы перевели число в двоичную систему, мы можем визуализировать его для лучшего понимания. Для этого используется обычно таблица, где каждая цифра двоичного числа размещается в отдельной ячейке.
Начиная с самого правого разряда двоичного числа, мы записываем его цифры слева направо. Если цифр в числе меньше разрядности, мы заполняем пустые разряды нулями. Например, если наше двоичное число имеет 8 разрядов, а исходное число состоит из 4 цифр, мы заполняем первые 4 разряда нулями.
Для примера возьмем число 42, которое в десятичной системе имеет следующее представление: 00101010. В таблице это будет выглядеть следующим образом:
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
Такая визуализация позволяет наглядно увидеть структуру двоичного числа и обращаться к отдельным его разрядам при необходимости.
Примеры

Ниже приведены несколько примеров конвертации чисел в двоичную систему счисления:
Пример 1:
Десятичное число: 25
Двоичное представление: 11001
Пример 2:
Десятичное число: 50
Двоичное представление: 110010
Пример 3:
Десятичное число: 128
Двоичное представление: 10000000
Пример 4:
Десятичное число: 0
Двоичное представление: 0
Пример 5:
Десятичное число: 1023
Двоичное представление: 1111111111
Используя приведенные выше примеры, вы можете легко научиться конвертировать числа в двоичную систему счисления.
Пример 1: Конвертация числа 10 в двоичную систему

Для конвертации числа 10 в двоичную систему, мы используем алгоритм деления числа на 2 и записи остатков. В данном примере мы начинаем с числа 10 и продолжаем делить его на 2 до тех пор, пока не получим нулевой результат.
10 ÷ 2 = 5, с остатком 0
5 ÷ 2 = 2, с остатком 1
2 ÷ 2 = 1, с остатком 0
1 ÷ 2 = 0, с остатком 1
Теперь мы записываем остатки в обратном порядке: 1010. Полученное число 1010 является двоичным представлением числа 10.