Нахождение точки касания графика с касательной – важная задача в математике и геометрии. Она позволяет определить точку пересечения между графическим представлением функции и ее касательной. Это может быть полезно, например, для определения скорости или изменения функции в конкретной точке.

Существует несколько методов, которые позволяют найти координаты точки касания графика с касательной. Один из таких методов - метод дифференцирования. Дифференцирование позволяет найти производную функции в заданной точке, которая является коэффициентом при x в уравнении касательной. Зная производную, мы можем найти уравнение касательной и найти координаты точки касания.

Еще один метод, который можно использовать для нахождения координаты точки касания графика с касательной, - метод аппроксимации. Он основан на приближении графика функции с помощью линейной функции (касательной). Для этого необходимо рассмотреть две близкие точки на графике функции и построить через них прямую линию. Эта прямая линия будет приближенно представлять касательную к графику в заданной точке, и мы сможем найти координаты точки касания.

Оба этих метода позволяют найти координаты точки касания графика с касательной, но каждый из них имеет свои особенности и применяется в разных случаях. Выбор метода зависит от конкретной задачи и предпочтений исследователя или инженера.

Методы нахождения точки касания графика и касательной

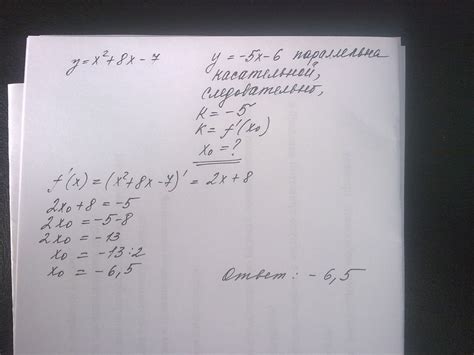
Существуют различные методы нахождения точки касания графика и его касательной. Один из наиболее распространенных методов - дифференцирование. Идея заключается в том, что касательная к графику функции имеет такой же наклон, как и касательная к кривой графика функции в данной точке. Дифференцирование позволяет найти угловой коэффициент касательной - производную функции в данной точке. Затем используется формула для нахождения уравнения прямой, проходящей через данную точку с известным угловым коэффициентом.

Еще одним методом нахождения точки касания является геометрический анализ. График функции и его касательная могут быть рассмотрены как две кривые, имеющие общую точку касания. Решение этого уравнения позволяет найти координаты точки касания.

Третий метод нахождения точки касания - алгебраический анализ. Уравнение функции и уравнение касательной могут быть записаны в алгебраической форме. Затем решение системы уравнений позволяет найти точку касания.

Выбор метода нахождения точки касания зависит от конкретной ситуации и требований к точности результата. Иногда для нахождения точки касания можно использовать несколько методов одновременно, чтобы повысить точность и достоверность результата.

Геометрический подход

Геометрический подход к нахождению координаты точки касания графика с касательной подразумевает использование геометрических свойств графика и касательной линии.

Для выполнения этого метода необходимо найти точку пересечения графика с касательной линией. Для этого можно воспользоваться следующим алгоритмом:

1. Найти уравнение касательной линии в точке, в которой требуется определить координату точки касания.
2. Найти точку пересечения графика с касательной линией путем решения системы уравнений, состоящей из уравнения графика и уравнения касательной линии.
3. Найти координату точки пересечения графика с касательной линией, которая будет являться координатой точки касания.

Геометрический подход позволяет точно определить координаты точки касания графика с касательной линией на основе геометрических свойств фигур. Однако для решения системы уравнений может потребоваться использование алгебраических методов, что может быть достаточно сложно.

При использовании геометрического подхода необходимо также обратить внимание на возможные особенности графика, такие как ось симметрии, вертикальные и горизонтальные асимптоты, и особые точки, которые могут влиять на процесс нахождения координаты точки касания.

Аналитический подход

Метод нахождения координаты точки касания графика с касательной с использованием аналитического подхода основан на использовании производной функции в данной точке.

Для начала необходимо найти производную исследуемой функции. Производная показывает наклон касательной к графику функции в каждой точке и позволяет найти координаты точек касания.

Пусть дана функция f(x) и точка (a, f(a)), в которой нужно найти касательную. Найдем производную функции f'(x) и вычислим ее значение в точке a. Полученное значение будет являться коэффициентом наклона касательной.

Теперь уравнение касательной к графику функции f(x) в точке (a, f(a)) можно записать в виде:

Где y - координата точки на касательной, x - ее абсцисса, f(a) - значение функции f(x) в точке a, f'(a) - значение производной функции f(x) в точке a.

Зная коэффициенты уравнения касательной, можно использовать его для нахождения других точек этой касательной или для анализа свойств графика функции в окрестности точки касания.

Численные методы

В контексте нахождения координаты точки касания графика с касательной численные методы могут быть использованы для приближенного решения этой задачи. Они позволяют аппроксимировать график функции и вычислять его производные в заданных точках.

Одним из таких численных методов является метод дихотомии. Он основан на применении итерационного процесса, который позволяет находить корни уравнений. В данном случае, можно использовать данный метод для приближенного нахождения координаты точки касания графика с касательной.

Другим методом, которые может быть применен для решения данной задачи, является метод Ньютона. Этот метод основан на аппроксимации функции касательной в заданной точке и нахождении ее корня с помощью итерационного процесса.

Таким образом, численные методы позволяют приближенно решать задачу нахождения координаты точки касания графика с касательной. Они являются эффективным инструментом для решения сложных математических задач, когда точного аналитического решения нет или его сложно найти.