Медианы треугольника - это линии, соединяющие вершины треугольника с серединами противоположных сторон. Пересечение медиан образует точку, называемую центроидом, которая обладает рядом интересных свойств и имеет важное значение в геометрии. Эта точка делит каждую из медиан в соотношении 2:1, то есть расстояние от вершины до центроида вдвое меньше, чем расстояние от центроида до середины противоположной стороны.
Существует несколько методов для определения координат центроида и пересечения медиан треугольника. Один из самых простых и распространенных методов - использование средних арифметических значений координат вершин треугольника. Для треугольника с вершинами A(x1, y1), B(x2, y2) и C(x3, y3) можно вычислить координаты центроида G(xg, yg) с помощью следующих формул:
xg = (x1 + x2 + x3) / 3
yg = (y1 + y2 + y3) / 3
Другой метод для определения координат центроида - использование координат векторов медиан. Координаты центроида можно выразить как сумму координат концов медиан, поделенную на 3:
xg = (x1 + x2 + x3)/3
yg = (y1 + y2 + y3)/3
Координаты пересечения медиан полезны для решения различных задач в геометрии. Они могут быть использованы для нахождения площади треугольника по формуле Герона, для построения окружности, описанной вокруг треугольника, и для нахождения расстояния от вершины треугольника до противоположной стороны. Координаты центроида также могут быть полезны при решении задач в физике, механике и других областях, где треугольник используется для моделирования различных систем.
Методы определения координат пересечения медиан треугольника
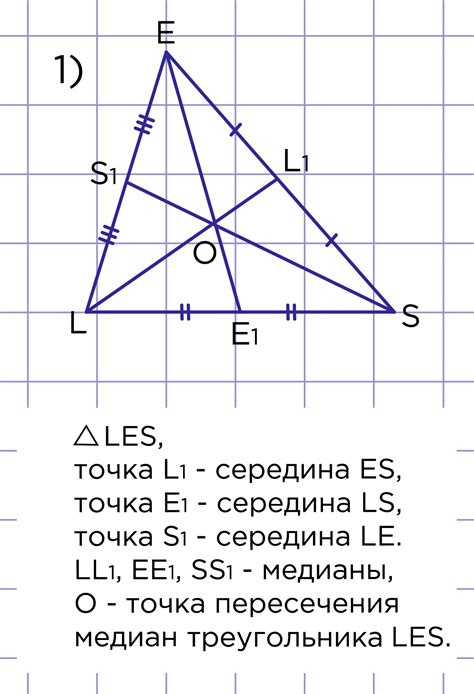
Существует несколько методов вычисления координат пересечения медиан треугольника.
- Метод координатных плоскостей: для каждой медианы находим уравнение прямой, затем составляем систему уравнений для пересечения этих прямых
- Метод векторных вычислений: находим вектора каждой медианы, затем составляем систему уравнений для пересечения этих векторов
- Метод использования геометрических свойств медиан: с использованием известных свойств медиан треугольника, таких как равенство площадей треугольников, можно вывести формулу для определения координат пересечения медиан
Для каждого метода необходимо знание координат вершин треугольника. С использованием любого из методов можно определить координаты пересечения медиан, их точность зависит от точности исходных данных и выбранного метода вычислений.
Знание координат пересечения медиан треугольника может быть полезным в различных областях, таких как геометрия, инженерия, компьютерная графика и другие.
Геометрический подход

Для рассчета координат пересечения медиан можно использовать геометрические свойства треугольника. Например, известно, что медиана, проведенная из вершины треугольника, делит противоположную сторону пополам. Также известно, что все три медианы пересекаются в одной точке, которая делится в отношении 2:1 относительно каждой медианы.
Для вычисления координат центра тяжести треугольника можно использовать координаты вершин треугольника. Пусть (x1, y1), (x2, y2) и (x3, y3) - координаты вершин треугольника. Тогда координаты центра тяжести можно найти следующим образом:
| Формула для нахождения координат x центра тяжести: | x = (x1 + x2 + x3) / 3 |
|---|---|
| Формула для нахождения координат y центра тяжести: | y = (y1 + y2 + y3) / 3 |
Итак, геометрический подход позволяет найти точное положение пересечения медиан треугольника при известных координатах его вершин. Этот метод широко используется в геометрии, картографии, компьютерной графике и других областях, где требуется нахождение центра тяжести многогранников.
Использование векторных вычислений

Векторные вычисления позволяют эффективно решать задачи, связанные с координатами пересечения медиан треугольника. Для расчета координат пересечения медиан можно использовать метод векторного произведения.
Для начала определим координаты вершин треугольника. Пусть A(x1, y1), B(x2, y2) и C(x3, y3) - координаты вершин треугольника ABC.
Затем найдем координаты точек пересечения медиан с помощью векторного произведения. Для этого нужно найти координаты векторных сумм медиан. Медианы - это отрезки, соединяющие вершины треугольника с серединами противоположных сторон.
Медианы можно найти по формуле:
Ma = (A + B)/2
Mb = (B + C)/2
Mc = (C + A)/2
Определим векторы AMa, BMb и CMc:
AMa = Ma - A
BMb = Mb - B
CMc = Mc - C
Теперь найдем векторное произведение векторов AMa и BMb:
AMa x BMb = [(y2 - y1)(0 - (y1 + y2)/2) - (0 - x1)((y1 + y2)/2 - y1)]
В результате получим координаты точки пересечения медиан M:
M(xm, ym) = M(x1 + (x2 - x1)/2, y1 + (y2 - y1)/2)
Аналогично находим координаты точки пересечения медиан M2:
M2(xm2, ym2) = M2(x2 + (x3 - x2)/2, y2 + (y3 - y2)/2)
И координаты точки пересечения медиан M3:
M3(xm3, ym3) = M3(x3 + (x1 - x3)/2, y3 + (y1 - y3)/2)
Таким образом, с помощью векторных вычислений можно быстро и точно определить координаты пересечения медиан треугольника.
Применение координат пересечения медиан

1. Геометрические вычисления
Позиция точки пересечения медиан может быть вычислена с использованием формул для нахождения координат центра тяжести треугольника. Эти вычисления основаны на средних значениях координат вершин треугольника. Такие вычисления могут быть полезными, когда требуется определить положение какой-либо точки внутри треугольника или проверить, лежит ли точка внутри треугольника.
2. Конструирование графиков
Графическое представление данных в виде координат пересечения медиан может быть полезным в различных областях. Например, в анализе данных и статистике можно использовать эту информацию для визуализации распределения данных, выделения центра тяжести или определения направлений эволюции.
3. Инженерные расчеты
В инженерных расчетах координаты пересечения медиан могут использоваться для определения геометрических характеристик конструкций. Например, они могут позволить определить центр тяжести системы масс в конструкции или рассчитать распределение нагрузок на определенную часть конструкции.
В общем, знание координат пересечения медиан треугольника может быть полезным в разнообразных задачах, связанных с геометрией, статистикой, инженерией и других областях.