Корень a в функции x – разнообразные методы и практические примеры использования

Корень является одной из самых важных математических операций, которая находит широкое применение в различных областях науки и техники. Корень a в функции x - это способ найти число, которое при возведении в степень x даст число a. Эта операция может быть представлена различными способами и имеет множество применений.

Основной способ обозначить корень - использование символа √ перед числом. Например, √25 означает корень числа 25. Извлечение корня из числа можно представить в виде выражения: x = √a. Это означает, что при возведении числа x в степень 2 мы получим число a.

Одной из основных задач в использовании корня в функции x является нахождение значения по известному числу и степени. Например, если нужно найти число, которое при возведении в квадрат даст 25, мы можем использовать корень: x = √25. Результатом будет число 5, так как 5 в квадрате даёт 25.

Корень a в функции x: интродукция

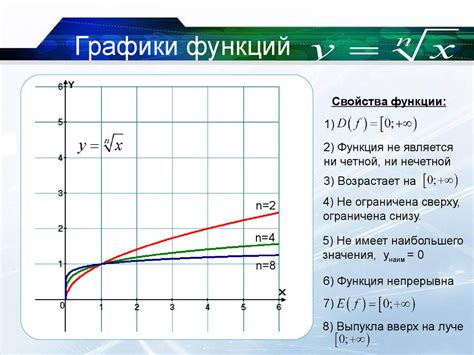
Корень a в функции x имеет широкий спектр применения и находит свое применение в различных областях науки и техники, включая физику, экономику, инженерию и программирование. Вычисление корня a в функции x может помочь в решении задач, связанных с оптимизацией производства, предсказанием трафика на дорогах, анализом финансовых данных и многими другими.

Существуют различные способы нахождения корня a в функции x, включая аналитические методы, численные методы и методы интерполяции. Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода зависит от конкретной задачи и требований пользователя.

Для лучшего понимания принципа нахождения корня a в функции x, рассмотрим примеры использования этого понятия. Например, при решении задачи оптимизации производства можно использовать корень a, чтобы найти оптимальное значение переменной x, при котором функция, описывающая производственные затраты, достигает минимума. Аналогично, при анализе финансовых данных можно использовать корень a, чтобы найти значения переменной x, при которых функция, описывающая доходность инвестиций, равна нулю, что поможет определить точку безубыточности.

Формула для расчета корня a в функции x

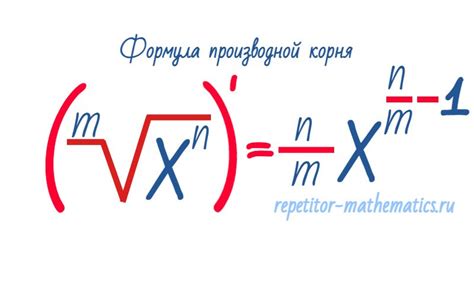
Корень a в функции x часто используется при решении различных математических задач. Расчет корня a позволяет найти значение x, при котором функция равна a. Для этого существует специальная формула, которая выражает зависимость между корнем a и функцией x.

Формула для расчета корня a в функции x выглядит следующим образом:

x = a^(1/2)

Данная формула означает, что значение x, при котором функция равна a, можно получить путем возведения числа a в степень 1/2, то есть взятием квадратного корня из a.

Пример использования данной формулы:

Пусть дано уравнение x^2 = 25, где необходимо найти значения x. В данном случае, функция x^2 равна 25, поэтому a = 25. С помощью формулы для расчета корня a в функции x, получаем:

x = 25^(1/2)

Результатом данного выражения является число 5, так как 5^2 = 25. Таким образом, уравнение x^2 = 25 имеет два решения: x = 5 и x = -5.

Формула для расчета корня a в функции x является удобным математическим инструментом, который позволяет находить значения переменной x при заданных функциях. Она часто применяется в различных областях науки, инженерии и финансах для решения задач и оптимизации процессов.

Способ 1: Использование библиотечной функции

Для вычисления корня a в функции x можно воспользоваться библиотечной функцией с возведением в степень 1/a. Такой подход позволяет достичь точного значения корня, используя готовую математическую функцию, предоставляемую языком программирования или сторонней библиотекой.

Пример использования:

В этом примере мы импортировали модуль math и использовали функцию pow() для вычисления корня. Аргументами функции являются значение a и степень, в которую необходимо возвести аргумент. В данном случае мы возвели a в степень 1/2, что равносильно вычислению квадратного корня. Результатом вычислений является значение x, которое равно корню из a.

Способ 2: Итерационный метод

Основная идея итерационного метода заключается в том, что исходное приближение к корню уточняется на каждой итерации. Для этого используется некоторая итерационная формула, которая позволяет получить более точное значение корня. Чем больше количество итераций, тем более точное значение корня можно получить.

Применение итерационного метода требует определения итерационной формулы, которая зависит от конкретной функции и условий задачи. Некоторые из наиболее распространенных итерационных методов включают метод Ньютона, метод простой итерации и метод бисекции.

Для примера рассмотрим метод простой итерации. В этом методе используется следующая итерационная формула:

1. Выберем начальное приближение корня a, например, a = 1.
2. Выполним итерационную формулу: a_n+1 = f(a_n), где f(x) - функция, корень которой мы ищем.
3. Повторяем шаг 2 до тех пор, пока значение a_n+1 не станет достаточно близким к a_n.
4. Полученное значение a_n является приближенным значением корня a.

Итерационный метод является достаточно простым и гибким подходом к нахождению корня a в функции x. Он широко применяется в различных областях, таких как математика, физика, экономика и т.д. Использование итерационного метода позволяет получить достаточно точные значения корня при условии правильного выбора итерационной формулы и начального приближения.

Примеры использования

Использование функции корня a в программировании может быть полезным во многих случаях. Вот несколько примеров:

1. Расчет стандартного отклонения: для вычисления стандартного отклонения необходимо возвести каждое значение в квадрат, затем просуммировать все значения и взять квадратный корень из полученной суммы. Функция корня a поможет в этом расчете.

2. Вычисление среднего геометрического: среднее геометрическое - это корень a из произведения всех значений. Функция корня a позволит нам вычислить это значение.

3. Решение квадратного уравнения: в общем виде, квадратное уравнение задается вида ax^2 + bx + c = 0, где a, b и c - известные коэффициенты. Функция корня a позволит нам найти корни этого уравнения.

4. Определение расстояния между двумя точками: функция корня a позволяет нам вычислить расстояние между двумя точками по формуле d = √((x2-x1)^2 + (y2-y1)^2).

Все эти примеры демонстрируют, что использование функции корня a может быть весьма полезным в решении различных задач, связанных с математикой и программированием.