Корень числа – это математическая операция, обратная возведению в степень. Она позволяет найти число, которое при возведении в указанную степень даст исходное число. Корень можно вычислить различными способами – аналитически или приближенно, используя формулы или численные методы. Знание этих способов и формул позволяет с легкостью решать задачи, связанные с извлечением корня.
Для вычисления корня числа можно использовать формулу, основанную на связи между корнем и степенью. Если мы хотим найти корень n-ной степени из числа a, то вычисление можно произвести с помощью формулы:
кореньn из a = a1/n
Таким образом, возведение в степень является обратной операцией к извлечению корня. Если мы возведем число в степень, а затем извлечем из результата корень соответствующей степени, мы получим исходное число. Например, извлекая квадратный корень из числа 9, мы получим 3, так как 3 в квадрате равно 9.
Что такое корень числа и зачем он нужен
Корень числа оказывается полезным во многих областях математики и естественных наук. Например, в геометрии он помогает находить длину сторон в задачах, связанных с прямоугольными треугольниками. В физике и инженерии корень помогает решать задачи электрических цепей или определять среднее значение физической величины.
Вычисление корня числа может быть осуществлено различными способами, в зависимости от требуемой точности и сложности самого числа. Численные методы, такие как метод Ньютона или метод бисекции, позволяют находить корни чисел в тех случаях, когда нет точной аналитической формулы. Однако для определенных чисел существуют простые формулы, позволяющие вычислить корень без использования численных методов.
Знание и понимание основ корня числа является важным элементом в математике и науке в целом. Непосредственное применение корня числа в реальных задачах позволяет получать точные и адекватные результаты, что делает его неотъемлемой частью многих областей знания.
Способы вычисления корня числа

1. Метод итераций. Этот метод основан на последовательном приближении к искомому корню. Начиная с произвольного значения, на каждом шаге значение корня уточняется. Процесс продолжается до тех пор, пока разность между полученным и ожидаемым значением не станет достаточно малой.
2. Метод Ньютона. Это итеративный метод, который использует производные исходной функции для нахождения корня. Начиная с произвольного значения, метод Ньютона стремится найти лучшую оценку корня, используя информацию о тангенсе угла наклона касательной к кривой функции в данной точке.
3. Метод деления отрезка пополам. Этот метод основан на идее, что если функция знакопеременна на концах отрезка, то она имеет корень на этом отрезке. Отрезок последовательно делится пополам до тех пор, пока разность значений на концах отрезка не станет достаточно малой.
4. Использование математических формул. Для некоторых конкретных случаев, таких как корень квадратный, кубический и т.д., существуют математические формулы, позволяющие вычислить корень числа без необходимости проводить итерации или делить отрезок пополам.
Выбор метода вычисления корня числа зависит от конкретной задачи и требуемой точности. Некоторые методы могут давать быстрые и точные результаты для определенных типов функций и чисел, в то время как другие могут быть менее эффективными или требовать большего количества вычислительных ресурсов.
Метод нахождения корня числа в степенной форме
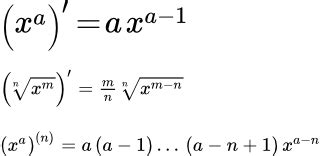
Существует несколько способов вычисления корня числа в степенной форме:
- Метод возведения в степень с последующим приближением: данный метод заключается в последовательном возведении числа в степень и проверке полученного значения. Для увеличения точности результатов можно использовать метод Ньютона или метод биссекции.
- Метод итераций: данный метод заключается в последовательных итерациях с использованием формулы, позволяющей приближенно найти корень числа в степенной форме. Существуют различные формулы и алгоритмы для применения этого метода.
- Метод интерполяции: данный метод основан на интерполяции функции, заданной для нахождения корня числа. Он заключается в аппроксимации исходной функции и нахождении нуля этой аппроксимации.
Выбор метода нахождения корня числа в степенной форме зависит от точности и скорости вычислений, а также от требований к результатам.
При использовании любого из указанных методов необходимо учитывать особенности чисел, с которыми работает алгоритм. Например, для вычисления корня отрицательного числа можно использовать комплексные числа или заменить их на положительные через применение модуля.
Итерационный метод вычисления корня числа

Для вычисления корня числа с помощью итерационного метода применяется формула:
xn+1 = (xn + a/xn) / 2
где xn+1 – новое приближение к корню, xn – предыдущее приближение, a – число, корень которого вычисляется.
Итерационный метод начинается с выбора произвольного начального приближения x0 и последовательного обновления приближений согласно формуле. Чем больше количество итераций, тем более точное значение корня будет получено.
Преимущество итерационного метода заключается в его простоте и универсальности. Он может быть применен для вычисления корня любого числа, в том числе и чисел, которые нельзя выразить аналитически.
Однако итерационный метод также имеет недостатки. Некоторые корни могут сходиться медленно или вовсе не сходиться. Поэтому необходимо следить за точностью вычислений и остановиться, когда достигнута нужная точность.
Метод Ньютона вычисления корня числа

Данный метод основывается на следующей идее: если у нас есть начальное приближение корня числа, то мы можем найти лучшее приближение, используя формулу:
| Формула | Вычисление |
|---|---|
| xn+1 = xn - f(xn)/f'(xn) | Новое приближение = Предыдущее приближение - (Значение функции в предыдущем приближении) / (Значение производной функции в предыдущем приближении) |
Здесь xn - предыдущее приближение, xn+1 - новое приближение, f(xn) - значение функции в предыдущем приближении, f'(xn) - значение производной функции в предыдущем приближении.
Процесс продолжается, пока разница между предыдущим и новым приближениями не станет достаточно маленькой, то есть пока мы не достигнем желаемой точности.
Метод Ньютона позволяет вычислить корень числа с высокой точностью и эффективностью. Однако, для его применения необходимо знание значение производной функции в каждой итерации, что может быть сложной задачей в некоторых случаях.
Формулы для вычисления корня числа

1. Квадратный корень - это наиболее распространенная форма корня, которая обозначается символом √. Формула для вычисления квадратного корня следующая: √a = b, где a - число, b - квадратный корень из числа a.
2. Кубический корень - это корень степени 3, и обозначается символом ∛. Формула для вычисления кубического корня выглядит так: ∛a = b, где a - число, b - кубический корень из числа a.
3. Натуральный логарифм - это форма корня, вычисляемая с использованием натурального логарифма. Формула для вычисления натурального логарифма корня числа выглядит следующим образом: ln(a) = b, где a - число, b - натуральный логарифм корня числа a.
4. Общий корень - это корень любой степени n, и обозначается символом √n. Формула для вычисления общего корня имеет вид: √n x¹/n = b, где x - число, n - степень корня, b - общий корень из числа x.
Формулы для вычисления корня чисел играют важную роль в математике и ежедневной жизни, позволяя нам решать различные задачи, связанные с извлечением корней чисел.
Формула для вычисления квадратного корня

Для вычисления квадратного корня применяется специальная формула √x = y, где x - число, из которого требуется извлечь корень, а y - сам корень. Для простоты расчетов применяется ряд методов, которые позволяют приближенно находить значение корня.
Одним из наиболее распространенных методов является метод Ньютона, также известный как метод касательных. Для этого используется следующая формула: y0 = (x0 + x / x0) / 2, где y0 - первое приближение к корню, x0 - число, из которого извлекается корень.
Еще одним часто используемым методом является метод Дичле, также известный как метод деления пополам. Для вычисления квадратного корня используется следующая формула: y0 = (a + b) / 2, где y0 - первое приближение к корню, a и b - два числа, между которыми находится корень.
В зависимости от точности, требуемой для вычисления квадратного корня, можно применять различные методы и формулы. Поэтому важно учитывать конкретную задачу и выбрать наиболее подходящий способ вычисления корня.
Формула для вычисления кубического корня

Формула для вычисления кубического корня имеет вид:
- Если число положительное: ∛a = a1/3
- Если число отрицательное: ∛a = -(-a)1/3
В первом случае кубический корень берется из положительного числа, а во втором случае – из отрицательного числа. Важно помнить, что кубический корень из отрицательного числа является комплексным числом.
Формула позволяет вычислить кубический корень любого числа, включая иррациональные числа. Она основана на алгоритме возведения в степень и может быть использована для подсчета кубического корня вручную или с использованием калькулятора.