Феномен корня из 1 равен 1 является одним из интересных математических явлений, которые могут вызывать смущение и вопросы у студентов, только начинающих осваивать базовую алгебру.
Однако, несмотря на то что данный феномен может показаться парадоксальным или даже противоречивым, его объяснение на самом деле довольно простое. Корень из 1 по определению равен тому числу, которое при возведении в квадрат дает 1.
Таким образом, если мы возведем число 1 в квадрат, мы получим 1. То есть 1 * 1 = 1. Из этого следует, что корень из 1 равен 1, так как есть только одно число, возведение которого в квадрат дает 1.
Феномен корня из 1

В математике, корень числа является величиной, возведение которой в некоторую степень дает исходное число. Но что произойдет, если мы возведем число 1 в некоторую степень? Все степени будут равны 1, в том числе и степень, равная 1/2, что соответствует взятию квадратного корня.
Для большинства чисел, взятие корня из соответствующего числа будет иметь место только в случае, когда это число положительное. Но для числа 1 есть исключение. Взятие корня из 1 дает нам всегда 1, будь то обычный корень, квадратный корень, кубический корень или любой другой корень.
Этот феномен имеет как теоретическое, так и практическое значение. Он заключает в себе идею единицы, которая является базовой и всеобъемлющей в математике. Единица – это исходный элемент, от которого мы отталкиваемся при построении всей системы чисел. Феномен корня из 1 говорит нам, что даже после множества математических операций, мы всегда возвращаемся к исходной точке – единице.
Этот факт играет важную роль в различных областях математики и физики, таких как теория чисел, алгебра, геометрия, электричество и многих других. Также это является основой для доказательств и формулировок математических теорем и законов.
Таким образом, феномен корня из 1 является неотъемлемой частью математического мира. Он показывает, что даже самые простые и очевидные вещи могут иметь глубокий смысл и оказывать значительное влияние на различные области знания.
Математический феномен

Корень из единицы, обозначаемый как √1 или 1^1/2, равен одному. Это может показаться странным, поскольку мы можем подумать, что корни рассчитываются путем извлечения квадратного, кубического или другого корня числа. Однако, несмотря на это, корень из единицы равен ровно одному.
Этот феномен может быть объяснен с помощью свойств математической операции возведения в степень. Когда мы возводим число в некоторую степень, мы умножаем это число само на себя столько раз, сколько указано в показателе степени. Таким образом, 1^1/2 означает умножение единицы самой на себя половину раза.
Очевидно, что умножение числа само на себя половину раза равносильно умножению числа само на себя один раз. Поэтому корень из единицы равен одному.
Этот математический феномен демонстрирует, как математика может иногда приводить к удивительным и неожиданным результатам. Важно помнить, что математика строится на логике и строгих правилах, и даже кажущиеся необычными результаты имеют свое обоснование.
Геометрическое представление
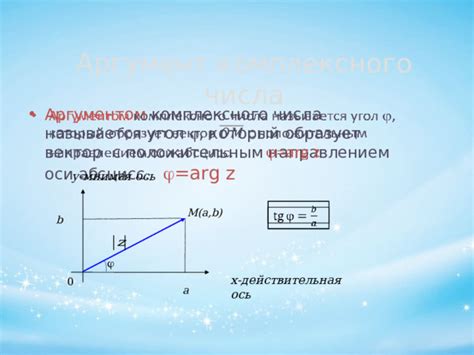
Чтобы лучше понять, почему корень из 1 равен 1, можно воспользоваться геометрическим представлением числа 1 на комплексной плоскости.
Комплексная плоскость представляет собой плоскость, на которой числа представлены в виде точек с двумя координатами: реальной и мнимой частью. Реальная ось представляет вещественные числа, а мнимая ось – мнимые числа.
Число 1 можно представить на комплексной плоскости как точку, которая находится на расстоянии 1 от начала координат и лежит на положительной вещественной оси. Это точка (1, 0).
Теперь представим, что мы возводим число 1 в какую-либо степень. Например, возведение в степень 2: 1^2 = 1 * 1 = 1. В геометрическом представлении означает, что мы умножаем точку (1, 0) на саму себя. Результатом будет та же самая точка (1, 0), так как умножение на 1 не изменяет положения точки.
Аналогично, при возведении числа 1 в любую положительную степень, мы всегда получим точку (1, 0). Это объясняет, почему корень из 1 равен 1 – это геометрический факт, который можно легко представить на комплексной плоскости.
Геометрическое представление позволяет наглядно увидеть, что число 1 является особенным и не меняется при возведении в любую нечетную положительную степень.
Примеры иллюстрирующие феномен
Феномен, при котором корень из 1 равен 1, можно проиллюстрировать на примере следующих математических операций:
1. Возведение числа 1 в любую степень всегда дает результат равный 1:
12 = 1
13 = 1
110 = 1
И так далее.
2. Умножение числа 1 на любое другое число также дает результат, равный этому числу:
1 * 2 = 2
1 * 3 = 3
1 * (-5) = -5
И так далее.
3. Деление числа на само себя всегда равно 1:
1 / 1 = 1
2 / 2 = 1
4 / 4 = 1
И так далее.
Такие примеры иллюстрируют феномен, при котором корень из 1 равен 1 и подтверждают его справедливость в математике.
Связь с комплексными числами

Комплексные числа - это числа, состоящие из двух частей: действительной и мнимой. Действительная часть представляет обычное вещественное число, а мнимая часть обозначается буквой i и представляет собой "мнимую единицу".
Мнимая единица i обладает свойством i^2=-1, то есть квадрат мнимой единицы равен -1. Используя это свойство, можно получить корень из -1, который обозначается как i. Также можно заметить, что i^4=(i^2)^2=1^2=1.
Из этого следует, что корни из единицы могут быть найдены как множество {1, -1, i, -i}, так как возведение каждого из этих чисел в четвертую степень дает 1.
Связь между корнем из 1 и комплексными числами заключается в том, что корень из 1 является частным случаем комплексных чисел. В комплексной плоскости, корни из 1 представлены вершинами регулярного многоугольника. Например, корень из 1 равен 1, корень из -1 равен -1, корень из i равен i и т. д.
Таким образом, корень из 1 равен 1 в контексте комплексных чисел из-за свойств мнимой единицы и возведения в четвертую степень.
Практическое применение феномена

Феномен, заключающийся в том, что корень из 1 равен 1, имеет множество практических применений в математике и науке. Одно из таких применений связано с решением уравнений и функций.
Во-первых, важно учитывать, что корень из 1 равен 1, это можно использовать при решении квадратных уравнений. Например, если имеется уравнение вида x^2 = 1, то мы знаем, что возможны два варианта решения: x = 1 или x = -1.
Во-вторых, данное свойство может применяться при вычислении значений функций. Например, если имеется функция f(x) = √(x^2), то при подстановке значения 1 вместо x мы получим результат равный 1.
Кроме того, обратимся к практическим применениям феномена в физике. Например, при вычислении силы тока в цепи по закону Ома, мы можем рассмотреть случай, когда сопротивление равно 1 Ом. Тогда, сила тока будет равна разности потенциалов между двумя точками на цепи.
Практическое применение феномена также находится в геометрии. Например, при вычислении длины стороны квадрата, мы можем применить факт, что у каждого квадрата все стороны равны друг другу и равны длине стороны равной 1. Таким образом, при подсчете периметра квадрата можно просто умножить значение стороны на 4.
Таким образом, практическое применение феномена, заключающегося в равенстве корня из 1 равен 1, широко используется в математике, науке и других областях знаний.



