В математике иногда возникают ситуации, когда необходимо найти корень из нецелого числа. Это может быть задача из физики, экономики или любой другой области, где точность является важным фактором. Решение такой задачи требует определенных знаний и навыков, и в данной статье мы рассмотрим гайд и различные способы решения этой проблемы.

Первый и самый простой способ - использование калькулятора с функцией вычисления корня. В большинстве современных калькуляторов есть такая функция, и ее использование не вызывает особых трудностей. Достаточно ввести число, из которого нужно найти корень, и нажать соответствующую кнопку. Однако, при использовании калькулятора нужно быть внимательным, чтобы не допустить ошибок при вводе данных или выборе функции.

Второй способ - использование математического программного обеспечения, такого как MATLAB или Wolfram Alpha. Эти программы предоставляют мощные средства для работы с математическими вычислениями и способны решить задачу с корнем из нецелого числа с высокой точностью. Однако, их использование требует определенных навыков программирования и знания синтаксиса соответствующего языка.

Третий способ - использование численных методов. Один из таких методов - метод Ньютона, который позволяет найти корень уравнения с заданной точностью. Для его применения необходимо иметь функцию, уравнение которой нужно решить, а также значение начального приближения. Метод Ньютона является итерационным, то есть требует нескольких шагов для достижения нужной точности. Однако, его использование может быть сложным и требует определенных математических знаний.

Как решить задачу с корнем из нецелого числа? Гайд и способы

1. Методы численного анализа:

• Метод Ньютона: этот метод позволяет найти приближенное значение корня нецелого числа. Для его применения нужно задать начальное приближение и последовательно уточнять результат, пока не будет достигнута желаемая точность.

• Метод деления отрезка пополам: этот метод основан на теореме Больцано-Коши и позволяет найти корень числа, если оно удовлетворяет условию неравенства. Для его применения нужно задать начальный отрезок, где находится корень, и далее последовательно делить отрезок пополам, выбирая ту его часть, на которой выполняется условие неравенства.

2. Методы аналитической геометрии:

• Графический метод: при помощи графика функции можно найти приближенное значение корня нецелого числа. Для этого строится график функции, заданной уравнением, и находится точка пересечения графика с осью абсцисс.

• Аналитический метод: этот метод основан на аналитическом решении уравнения, содержащего корень нецелого числа. Для его применения нужно привести уравнение к виду, где корень выражен явно, и найти его значение.

Решение задачи с корнем из нецелого числа может потребовать применения комбинации разных методов и техник в зависимости от поставленной задачи и доступных ресурсов. Важно выбрать наиболее подходящий метод для конкретной ситуации и выполнить необходимые вычисления с высокой точностью.

Алгоритм для вычисления квадратного корня из нецелого числа

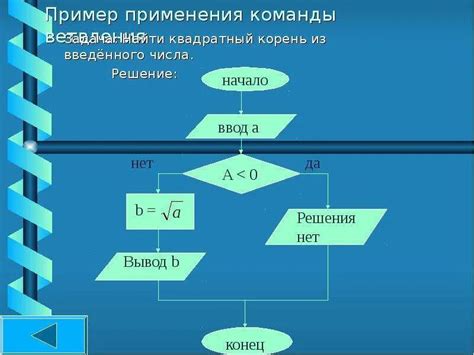
Алгоритм Ньютона использует итеративный подход для приближенного нахождения корня. Он основан на простой идее: если мы начинаем с некоторого начального приближения к корню, то на каждой итерации можно получить более точное приближение путем уточнения этого приближения.

Алгоритм Ньютона для вычисления квадратного корня можно описать следующим образом:

1. Выберите начальное приближение к корню (например, половина исходного числа).
2. Вычислите новое приближение к корню, используя формулу: x = (x + (n / x)) / 2, где x - текущее приближение, n - исходное число.
3. Повторяйте шаг 2 до достижения желаемой точности.

Начав с достаточно хорошего начального приближения, алгоритм Ньютона может сходиться к корню с высокой точностью даже за несколько итераций. Он часто используется в различных математических библиотеках и языках программирования.

Подводя итог, алгоритм Ньютона представляет собой эффективный способ вычисления квадратного корня из нецелого числа. Он прост в реализации и обеспечивает высокую точность при достаточном количестве итераций.

Метод Ньютона для вычисления корня из нецелого числа

Метод Ньютона предоставляет один из способов вычисления корня из нецелого числа. Этот метод основан на итерационном подходе, который позволяет приближенно находить значение корня числа.

Следуя методу Ньютона, можно получить приближенное значение корня из нецелого числа. Начиная с некоторого начального приближения, метод Ньютона использует формулу:

x_n+1 = x_n - f(x_n)/f'(x_n)

где x_n - n-ое приближение корня, f(x_n) - значение функции в точке x_n и f'(x_n) - значение производной функции в точке x_n.

Процесс продолжается до тех пор, пока значение приближения удовлетворяет заданной точности или требованиям. Чем больше количество итераций, тем более точное значение корня получается.

Одним из ключевых преимуществ метода Ньютона является его скорость сходимости. Однако следует отметить, что этот метод может привести к ошибкам, если начальное приближение выбрано неправильно или функция имеет особенности.

Приведем пример использования метода Ньютона для вычисления корня из нецелого числа:

1. Задаем начальное приближение корня.
2. Вычисляем значение функции в точке начального приближения.
3. Вычисляем значение производной функции в точке начального приближения.
4. Используем формулу метода Ньютона для получения нового приближенного значения корня.
5. Повторяем шаги 2-4 до достижения необходимой точности.

Таким образом, метод Ньютона является эффективным инструментом для вычисления корня из нецелого числа. Зная начальное приближение и точность, можно получить точное (или приближенное) значение корня, что может быть полезно в различных областях науки и техники.

Использование библиотек для вычисления корня из нецелого числа

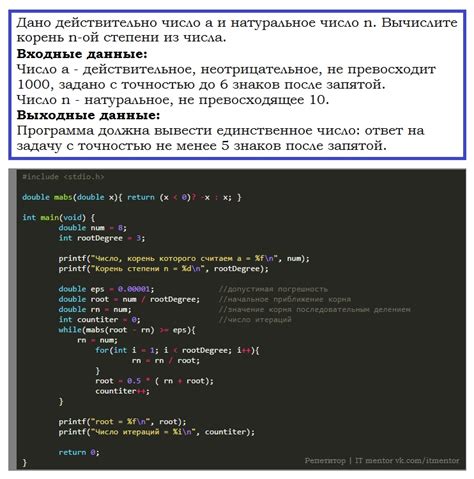
Решение задачи с вычислением корня из нецелого числа может быть достигнуто при помощи различных библиотек программирования, которые предоставляют готовые функции для выполнения данной операции.

Одной из таких библиотек является math в языке программирования Python. Для вычисления корня из нецелого числа можно использовать функцию sqrt(), которая возвращает квадратный корень заданного числа. Например:

import math
number = 5.5
root = math.sqrt(number)
print("Квадратный корень из числа", number, "равен", root)

Также в языке программирования Java можно воспользоваться классом Math, который содержит метод sqrt() для вычисления квадратного корня нецелого числа. Пример использования:

import java.lang.Math;
public class Main {
public static void main(String[] args) {
double number = 5.5;
double root = Math.sqrt(number);
System.out.println("Квадратный корень из числа " + number + " равен " + root);
}
}

Другим примером является язык программирования JavaScript, в котором также существуют функции для вычисления корня из нецелого числа. Одной из таких функций является Math.sqrt(). Пример использования:

let number = 5.5;
let root = Math.sqrt(number);
console.log("Квадратный корень из числа", number, "равен", root);

Подобные библиотечные функции позволяют упростить процесс вычисления корня из нецелого числа и получить точный результат без необходимости вручную реализовывать алгоритмы для выполнения данной операции.

Примеры задач и их решения с использованием корня из нецелого числа

Пример 1: Расчет площади круга

Задача: Найти площадь круга с радиусом, равным 3.5 см.

Решение: Площадь круга можно рассчитать по формуле S = π * r^2, где π - число Пи (примерно равно 3.14159), r - радиус круга. В данной задаче радиус круга равен 3.5, поэтому заменяем r в формуле и подставляем значение числа Пи. Получаем S = 3.14159 * (3.5)^2 = 3.14159 * 12.25 = 38.48 (приближенно).

Пример 2: Расчет длины окружности

Задача: Найти длину окружности с радиусом, равным 2.8 метра.

Решение: Длину окружности можно найти по формуле C = 2 * π * r, где π - число Пи (примерно равно 3.14159), r - радиус окружности. В данной задаче радиус окружности равен 2.8, поэтому заменяем r в формуле и подставляем значение числа Пи. Получаем C = 2 * 3.14159 * 2.8 = 17.60 (приближенно).

Пример 3: Расчет стороны квадрата

Задача: Найти сторону квадрата, площадь которого равна 25 квадратных сантиметров.

Решение: Площадь квадрата можно найти по формуле S = a^2, где a - сторона квадрата. В данной задаче площадь квадрата равна 25, поэтому заменяем S в формуле и находим корень из полученного значения. Получаем a = √25 = 5.

Замечание: Во всех примерах предполагается, что заданные значения радиуса или площади положительные и ненулевые.

Рекомендации по выбору метода вычисления корня из нецелого числа

Одним из самых простых и распространенных методов для вычисления корня из нецелого числа является метод взятия корня с помощью калькулятора. Этот метод подходит для ситуаций, когда точность не является критически важной, и когда требуется быстрое приближенное значение корня.

Если точность является важным фактором, аналитический метод, такой как метод Ньютона, может быть предпочтительным. Этот метод позволяет найти более точное приближение корня, используя первоначальное приближение и итеративный процесс уточнения значения. Однако метод Ньютона требует больше времени и вычислительных ресурсов.

Для более сложных и обширных вычислений, когда необходимо вычислить корень из нецелого числа с большей точностью, можно использовать численные методы, такие как метод бисекции или метод Чебышева. Эти методы разбивают интервал на две части и находят корень в заданной точности.

Иногда, в зависимости от конкретной задачи, может быть разумным использование специализированных функций или библиотек, предоставляемых языком программирования или математическими программами. Например, в языке Python можно использовать функцию math.sqrt() для вычисления корня из числа.

Важно выбрать метод вычисления корня из нецелого числа, который наилучшим образом соответствует конкретной задаче, учитывая требуемую точность, доступные ресурсы и время выполнения. Экспериментирование с различными методами и тестирование их на реалистичных данных может помочь определить самый эффективный и точный способ вычисления корня из нецелого числа в заданной ситуации.