Квадратное уравнение является одним из фундаментальных понятий в математике. В его основе лежит квадратный трехчлен, который можно представить в виде ax^2 + bx + c = 0. Решение квадратного уравнения обычно связано с нахождением его корней. Корень уравнения - это значение переменной, при котором уравнение превращается в верное равенство.
Корни квадратного уравнения можно найти с помощью дискриминанта, который определяется по формуле D = b^2 - 4ac. Дискриминант позволяет изучать количество и характер корней уравнения. В случае, когда дискриминант равен нулю, уравнение имеет один корень.
Существует несколько методов нахождения корня квадратного уравнения с дискриминантом ноль. Один из самых простых способов - использование формулы корня, которая записывается как x = -b/2a. Эта формула позволяет найти значение корня уравнения без необходимости выполнения дополнительных вычислений.
Рассмотрим пример. Пусть дано квадратное уравнение 2x^2 + 4x + 2 = 0. Чтобы найти корень этого уравнения, сначала нужно определить его дискриминант. Подставим значения коэффициентов a, b и c в формулу дискриминанта: D = 4^2 - 4*2*2. Расчитаем значение дискриминанта: D = 16 - 16 = 0.
Определение квадратного уравнения

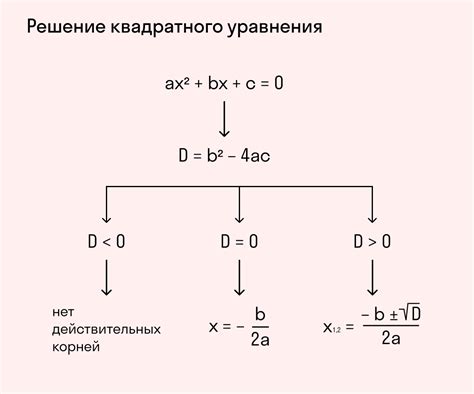
Квадратное уравнение может иметь три варианта решения:
| Вариант решения | Количество корней |
|---|---|
| Два различных корня | Дискриминант D > 0 |
| Один корень (корень кратности два) | Дискриминант D = 0 |
| Корней нет (комплексные корни) | Дискриминант D |
Дискриминант (D) квадратного уравнения можно вычислить по формуле: D = b^2 - 4ac.
Пример: Дано уравнение 2x^2 - 5x + 2 = 0.
Для определения количества корней и их значений, необходимо вычислить дискриминант:
D = (-5)^2 - 4 * 2 * 2 = 25 - 16 = 9.
Поскольку D > 0, значит, уравнение имеет два различных корня.
Понятие и формула квадратного уравнения
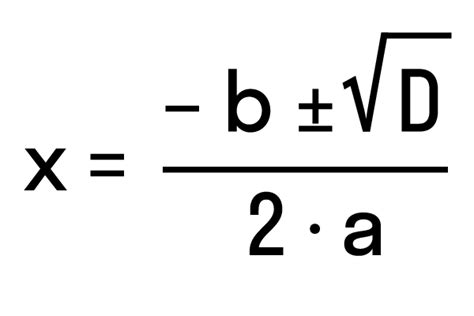
При решении квадратных уравнений применяется так называемая формула дискриминанта, которая позволяет определить количество и значения корней такого уравнения.
Дискриминант квадратного уравнения определяется по формуле: D = b2 - 4ac. Он высчитывается по коэффициентам уравнения.
Затем происходит проверка значения дискриминанта:
- Если D > 0, то квадратное уравнение имеет два различных вещественных корня.
- Если D = 0, то квадратное уравнение имеет один вещественный корень, который называется действительным корнем кратности два.
- Если D , то квадратное уравнение не имеет вещественных корней. На этом этапе можно определить, что корни уравнения будут комплексными числами.
Если получено значение дискриминанта, можно использовать другую формулу, чтобы найти корни уравнения:
Если D > 0, то корни уравнения найдутся по формуле: x1 = (-b + √D) / (2a) и x2 = (-b - √D) / (2a).
Если D = 0, то корень уравнения найдется по формуле: x = -b / (2a).
При D используется комплексная формула для нахождения корней: x1 = (-b + i√(-D)) / (2a) и x2 = (-b - i√(-D)) / (2a), где i – мнимая единица.
Зная значения коэффициентов a, b и c, можно использовать формулу дискриминанта и последующие расчеты, чтобы найти корни и решить квадратное уравнение.
Дискриминант квадратного уравнения
Дискриминант квадратного уравнения - это число, которое вычисляется по формуле: D = b2 - 4ac. Он играет важную роль при решении квадратных уравнений, так как позволяет определить, сколько действительных корней имеет уравнение.
Когда дискриминант равен нулю (D = 0), это означает, что квадратное уравнение имеет один действительный корень. Это можно использовать для нахождения этого корня с помощью формулы: x = -b/2a. Таким образом, решение уравнения будет иметь вид x = корень из D / 2a.
Пример:
Рассмотрим квадратное уравнение 2x2 - 4x + 2 = 0. Чтобы найти дискриминант, используем формулу: D = (-4)2 - 4*2*2 = 16 - 16 = 0.
Так как дискриминант равен нулю, уравнение имеет один действительный корень. Решим уравнение используя формулу: x = -(-4) / 2*2 = 4 / 4 = 1.
Таким образом, уравнение 2x2 - 4x + 2 = 0 имеет один корень x = 1.
Определение дискриминанта

Если дискриминант больше нуля, то квадратное уравнение имеет два различных действительных корня.
Если дискриминант равен нулю, то квадратное уравнение имеет один действительный корень. Этот корень называется «корнем кратности 2», так как он появляется дважды.
Если дискриминант меньше нуля, то квадратное уравнение не имеет действительных корней. В этом случае корни уравнения будут комплексными числами.
Знание значения дискриминанта позволяет анализировать квадратное уравнение на простоту или сложность решения, а также предсказать количество корней и их характеристики.
Связь дискриминанта с корнями уравнения

Дискриминант квадратного уравнения имеет важную связь с его корнями. Дискриминант определяет количество и тип корней уравнения и позволяет нам получить дополнительную информацию о его решениях. Рассмотрим несколько случаев:
- Когда дискриминант равен нулю, то уравнение имеет ровно один вещественный корень. Этот корень является двойным, то есть квадратное уравнение имеет два одинаковых решения.
- Когда дискриминант больше нуля, то уравнение имеет два различных вещественных корня. Эти корни можно найти с помощью формулы квадратного корня.
- Когда дискриминант меньше нуля, то уравнение не имеет вещественных корней. Однако, оно имеет комплексные корни, которые можно выразить в виде комплексных чисел.
Итак, дискриминант является индикатором числа корней и характеризует природу решений квадратного уравнения. Изучение дискриминанта позволяет нам более глубоко понять свойства и поведение корней квадратного уравнения.
Корни квадратного уравнения с дискриминантом ноль

Дискриминант, обозначаемый как D, играет важную роль в решении квадратных уравнений. Он вычисляется по формуле D = b2 - 4ac.
Если дискриминант равен нулю (D = 0), это означает, что уравнение имеет один корень. Корень такого уравнения называется "корнем кратности 2".
Чтобы найти корни квадратного уравнения с дискриминантом ноль, используется следующий метод:
1. Раскрываем скобки и приводим подобные члены в уравнении.
2. Приравниваем уравнение к нулю.
3. Решаем полученное линейное уравнение и находим значение корня.
Например, рассмотрим квадратное уравнение x2 - 6x + 9 = 0. В этом случае, дискриминант равен нулю: D = (-6)2 - 4(1)(9) = 0.
Выполним шаги для нахождения корня:
1. Раскроем скобки: x2 - 6x + 9 = 0.
2. Приравняем уравнение к нулю: x2 - 6x + 9 = 0.
3. Решим полученное линейное уравнение: x = 3.
Таким образом, уравнение x2 - 6x + 9 = 0 имеет один корень x = 3.
Методы нахождения корней с дискриминантом ноль

Когда дискриминант квадратного уравнения равен нулю, это означает, что уравнение имеет один корень. При этом корень совпадает с вершиной параболы, которую задает данное уравнение.
Для нахождения этого корня можно воспользоваться несколькими методами. Один из них - это метод зависимости от знака коэффициента при x2. Если этот коэффициент положителен, то корень будет отрицательным, а если отрицателен - корень будет положительным.
Другой метод - это метод выражения корня через коэффициенты уравнения. Если уравнение имеет вид ax2 + bx + c = 0, то корень можно выразить как x = -b/2a. Таким образом, с помощью данной формулы можно найти корень квадратного уравнения с дискриминантом ноль.
Пример использования этой формулы:
Уравнение: 3x2 - 6x + 3 = 0
Для нахождения корня, используя формулу x = -b/2a, нужно найти значения коэффициентов a и b. Подставив их в формулу, получим:
x = -(-6) / (2 * 3) = 6 / 6 = 1
Таким образом, корень квадратного уравнения 3x2 - 6x + 3 = 0 равен 1.
Примеры квадратных уравнений с дискриминантом ноль

Давайте рассмотрим несколько примеров квадратных уравнений с дискриминантом равным нулю.
- Уравнение x2 - 4x + 4 = 0
- Уравнение 2x2 + 4x + 2 = 0
Дискриминант этого уравнения равен нулю, так как D = (-4)2 - 4 * 1 * 4 = 0.
Чтобы найти корень данного уравнения, можно воспользоваться формулой: x = -b/2a.
В данном случае, a = 1 и b = -4, поэтому x = -(-4)/2*1 = 4/2 = 2.
Дискриминант этого уравнения также равен нулю, так как D = 42 - 4 * 2 * 2 = 0.
Применяя формулу для нахождения корня, получаем: x = -b/2a.
В данном случае, a = 2 и b = 4, следовательно, x = -4/2*2 = -4/4 = -1.
Таким образом, квадратные уравнения с дискриминантом равным нулю имеют один корень, который можно найти с помощью формулы x = -b/2a. Эти уравнения представляют собой особый случай и обладают свойством, что их графики касаются оси OX.