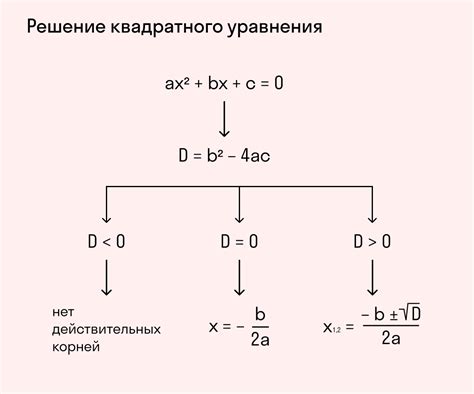
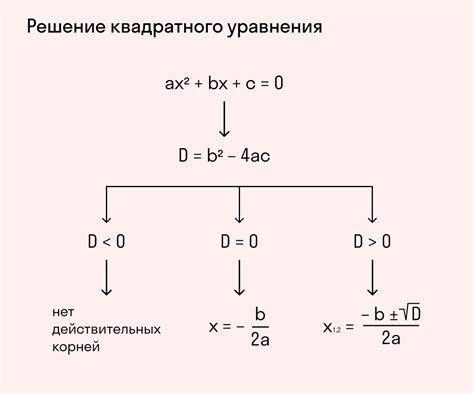
При решении квадратного уравнения вида ax^2 + bx + c = 0, одним из основных этапов является нахождение корней. Изучая дискриминант, мы можем определить тип решений этого уравнения и узнать, сколько корней оно имеет. Если дискриминант положительный, то у уравнения два различных вещественных корня. Если дискриминант равен нулю, то у уравнения один вещественный корень. Если дискриминант отрицательный, то у уравнения два комплексных корня.
Формула для вычисления дискриминанта имеет вид: D = b^2 - 4ac. Корень по дискриминанту представляет собой число, которое можно получить путем извлечения квадратного корня из дискриминанта. Имеет два знака - положительный и отрицательный. Положительный корень по дискриминанту используется при решении квадратного уравнения, а отрицательный корень по дискриминанту – при построении графика квадратной функции.
Существует несколько способов вычисления корня по дискриминанту. Во-первых, можно воспользоваться формулой: x = (-b ± √D) / (2a), где ± означает, что нужно рассмотреть два случая - с положительным и отрицательным значением корня. Во-вторых, можно использовать готовые решения, предоставляемые математическими программами и онлайн-калькуляторами. Такие инструменты позволяют быстро и точно вычислить корень по дискриминанту, не требуя излишних вычислительных усилий.
Что такое дискриминант?

Чтобы найти дискриминант квадратного уравнения, необходимо вычислить значение выражения, содержащегося под знаком радикала в формуле дискриминанта. Дискриминант обозначается буквой D и вычисляется следующим образом:
D = b2 - 4ac
- Если D < 0, то уравнение не имеет действительных корней;
- Если D = 0, то уравнение имеет один действительный корень, который является дважды кратным;
- Если D > 0, то уравнение имеет два различных действительных корня.
Дискриминант играет важную роль в изучении квадратных уравнений и находит применение в различных областях, таких как физика, экономика, техника и другие.
Определение понятия и его основные свойства
Дискриминант вычисляется по формуле: D = b^2 - 4ac. Он может принимать три значения:
| Значение дискриминанта | Характер решений уравнения |
|---|---|
| D > 0 | Уравнение имеет два различных вещественных корня |
| D = 0 | Уравнение имеет один вещественный корень |
| D < 0 | Уравнение не имеет вещественных корней |
В случае, когда дискриминант D >= 0, корень по дискриминанту определяется по следующей формуле: x = (-b ± √D) / (2a). Здесь знак ± означает, что нужно рассчитать два значения - с положительным и отрицательным знаком.
Основные свойства корня по дискриминанту:
- Корень по дискриминанту позволяет вычислить значения корней квадратного уравнения, если значение дискриминанта известно.
- Для положительного дискриминанта D > 0, уравнение имеет два различных вещественных корня.
- Для нулевого дискриминанта D = 0, уравнение имеет один вещественный корень.
- Для отрицательного дискриминанта D < 0, уравнение не имеет вещественных корней.
Зачем нужен дискриминант в квадратном уравнении?

Квадратное уравнение имеет вид:
ax2 + bx + c = 0,
где a, b и c - коэффициенты уравнения.
Дискриминант этого уравнения вычисляется по формуле:
D = b2 - 4ac.
- Если D > 0, то уравнение имеет два различных корня. При этом значение D указывает на количество корней.
- Если D = 0, то уравнение имеет один корень. В данном случае корни будут совпадать.
- Если D < 0, то уравнение не имеет действительных корней. В таком случае решение будет комплексным.
Таким образом, дискриминант позволяет нам определить, какие корни имеет квадратное уравнение и что делать дальше с этими корнями. Он является важным инструментом при решении квадратных уравнений и может помочь нам найти правильное решение.
Роль дискриминанта и его значение для решения уравнения

Дискриминант квадратного уравнения определяется по формуле: D = b^2 - 4ac, где a, b и c - коэффициенты уравнения.
Значение дискриминанта позволяет ответить на три основных вопроса:
- Если D > 0, то уравнение имеет два различных вещественных корня. Количество корней может быть определено по формуле: x1 = (-b + √D) / (2a) и x2 = (-b - √D) / (2a).
- Если D = 0, то уравнение имеет только один вещественный корень. Корень может быть найден по формуле: x = -b / (2a).
- Если D < 0, то уравнение не имеет вещественных корней, а имеет два комплексных корня. Действительная и мнимая части комплексных корней могут быть найдены по формуле: x1 = (-b + i√(-D)) / (2a) и x2 = (-b - i√(-D)) / (2a).
Таким образом, значение дискриминанта позволяет определить, сколько и какие корни имеет квадратное уравнение. Эта информация важна для решения уравнения и анализа его поведения в различных случаях.
Формула дискриминанта

Для квадратного уравнения вида ax^2 + bx + c = 0, дискриминант вычисляется по формуле:
D = b2 - 4ac
Если дискриминант больше нуля (D > 0), то квадратное уравнение имеет два действительных корня.
Если дискриминант равен нулю (D = 0), то квадратное уравнение имеет один действительный корень, который является двойным.
Если дискриминант меньше нуля (D < 0), то квадратное уравнение не имеет действительных корней.
Как вычислить дискриминант для квадратного уравнения
Формула для вычисления дискриминанта имеет вид:
Д = b² - 4ac
где a, b и c - коэффициенты квадратного уравнения.
Способы вычисления дискриминанта зависят от заданных коэффициентов:
1. Если коэффициент a равен нулю, то это уже не квадратное уравнение. Дискриминант становится неприменимым в этом случае.
2. Если a не равно нулю, но дискриминант положителен, то уравнение имеет два различных вещественных корня.
3. Если a не равно нулю, но дискриминант равен нулю, то уравнение имеет один вещественный корень, который является кратным.
4. Если a не равно нулю, но дискриминант отрицателен, то уравнение имеет два комплексных корня, которые являются сопряженными.
Теперь вы знаете, как вычислить дискриминант для квадратного уравнения и использовать его для определения характера корней. Это позволяет вам более точно решить уравнение и получить нужную информацию о его решениях.
Какова связь между дискриминантом и корнями уравнения?

Дискриминант вычисляется по формуле D = b² - 4ac, где a, b и c – коэффициенты квадратного уравнения ax² + bx + c = 0.
Если дискриминант больше нуля (D > 0), то уравнение имеет два различных действительных корня. Действительные корни будут расположены на числовой оси симметрично относительно вертикальной прямой, проходящей через вершину параболы.
Если дискриминант равен нулю (D = 0), то уравнение имеет ровно один действительный корень. Действительный корень будет являться вершиной параболы и будет находиться на числовой оси.
Если дискриминант меньше нуля (D < 0), то уравнение имеет два комплексных корня. Комплексные корни будут представлять собой пару сопряженных чисел и будут лежать в комплексной плоскости.
Таким образом, дискриминант позволяет не только определить количество корней уравнения, но и указать их тип и положение на числовой оси. Знание дискриминанта помогает более полно понять свойства и график квадратного уравнения.
Как использовать дискриминант для нахождения корней
Чтобы найти корни квадратного уравнения, необходимо выполнить следующие шаги:
- Вычислить дискриминант по формуле D = b^2 - 4ac.
- Определить тип корней по значению дискриминанта:
- Если D > 0, то уравнение имеет два действительных корня.
- Если D = 0, то уравнение имеет один действительный корень.
- Если D < 0, то уравнение имеет два комплексных корня.
- Вычислить корни уравнения, используя формулы:
- Если D > 0, то x1 = (-b + √D) / 2a и x2 = (-b - √D) / 2a.
- Если D = 0, то x = -b / 2a.
- Если D < 0, то x1 = (-b + i√|D|) / 2a и x2 = (-b - i√|D|) / 2a, где i - мнимая единица.
Теперь вы знаете, как использовать дискриминант для нахождения корней квадратного уравнения. Этот метод является универсальным и применим для любого квадратного уравнения. Не забывайте проверять полученные корни, подставляя их обратно в исходное уравнение и убеждаясь, что они удовлетворяют ему.
Когда дискриминант положителен?

Когда дискриминант положителен, то это означает, что у квадратного уравнения существуют два различных вещественных корня. Другими словами, уравнение имеет два решения.
Положительный дискриминант говорит о том, что квадратное уравнение имеет пересечение с осью абсцисс, то есть его график пересекает ось X в двух точках.
Значение дискриминанта отражает характер решений квадратного уравнения:
1. Если D > 0, то уравнение имеет два различных вещественных корня;
2. Если D = 0, то уравнение имеет один вещественный корень (корень кратности 2);
3. Если D < 0, то уравнение не имеет вещественных корней, а имеет два мнимых корня, которые представляют собой комплексные числа.