Реберный граф является одной из основных структур данных, используемых в теории графов. Он представляет собой набор вершин и ребер, связывающих эти вершины. Реберный граф широко применяется в различных областях, включая компьютерные науки, математику, сетевые технологии и многое другое.
Правильное построение реберного графа является важным этапом при решении различных задач, таких как поиск кратчайшего пути, определение связности графа и многих других. В данной статье мы рассмотрим основные шаги, которые необходимо выполнить для построения реберного графа.
Первым шагом при построении реберного графа является определение вершин и ребер. Вершины обозначаются числами или буквами, а ребра - парами вершин, которые они соединяют. Вторым шагом является рисование вершин и ребер в соответствии с заданными параметрами.
После рисования графа необходимо проверить его корректность. Для этого можно воспользоваться алгоритмами проверки связности, наличия циклов и других свойств графа. Если граф оказывается некорректным, необходимо внести соответствующие изменения и повторить процесс построения.
В этой статье мы рассмотрели основные шаги по правильному построению реберного графа. Эти шаги позволяют создать структуру данных, которая может быть использована для решения различных задач. Знание и понимание этих шагов является необходимым для всех, кто работает с графами и интересуется теорией графов.
Построение реберного графа: основы и практические примеры
Для построения реберного графа необходимо знать набор объектов и отношения между ними. Вершины графа представляют собой эти объекты, а ребра соединяют вершины, обозначая отношения между ними. Например, если объекты представляют города, то ребра могут указывать наличие дорог между городами или другие виды связей.
Построение реберного графа может быть выполнено вручную или с помощью программного обеспечения. Один из практических способов построения реберного графа - использование таблицы смежности. Таблица смежности представляет собой двумерную таблицу, где столбцы и строки соответствуют вершинам графа. Если есть связь между двумя вершинами, то в соответствующей ячейке ставится единица, в противном случае - ноль.
| Вершина 1 | Вершина 2 | Вершина 3 | |
|---|---|---|---|
| Вершина 1 | 0 | 1 | 1 |
| Вершина 2 | 1 | 0 | 0 |
| Вершина 3 | 1 | 0 | 0 |
В данном примере реберный граф содержит три вершины и представляет отношения между ними. Вершина 1 связана с вершинами 2 и 3, а вершины 2 и 3 не имеют других связей.
Построение реберного графа может быть усложнено, если имеются неориентированные связи или множественные ребра между вершинами. В таких случаях таблица смежности может быть заменена на другие структуры данных, такие как список смежности или матрица инцидентности.
Построение реберного графа может быть полезным инструментом для анализа и визуализации различных систем и процессов. Он позволяет легко представить сложные отношения и топологию сети в виде графа, что упрощает дальнейший анализ и принятие решений.
Что такое реберный граф?
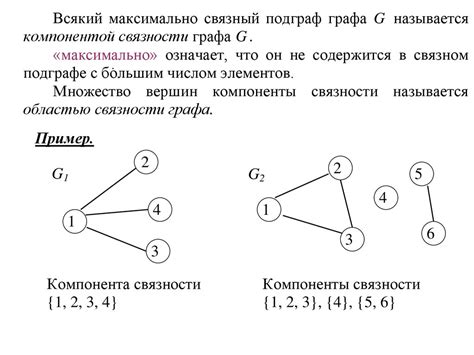
Ребра в графе могут быть направленными или ненаправленными. В случае направленного графа ребра имеют направление и связывают одну вершину с другой в определенном порядке. В ненаправленном графе ребра связывают вершины без задания направления.
Реберные графы широко используются в различных областях, таких как теория графов, сетевые технологии, оптимизация и транспортное планирование. Они могут быть использованы для моделирования различных явлений, описания взаимодействий между объектами или поиска оптимальных маршрутов.
Для построения реберного графа необходимо определить вершины и соединяющие их ребра. Вершины могут представлять собой географические объекты, узлы сети, пункты структуры или любые другие элементы, между которыми существуют связи или отношения. Ребра могут быть заданы в виде весов или меток, которые соответствуют определенным параметрам или характеристикам связей, таким как расстояние, пропускная способность или время передачи данных.
Как построить реберный граф?
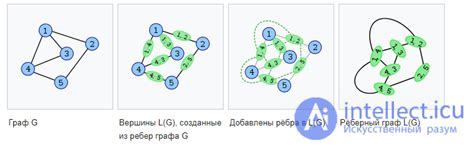
Шаг 1: Определение вершин графа
Вершины графа представляют отдельные элементы или объекты, которые требуется исследовать. Например, если мы анализируем систему социальных связей, то каждый человек будет представлять отдельную вершину графа.
Шаг 2: Определение ребер графа
Ребра графа представляют собой связи между вершинами. Необходимо определить, какие вершины связаны друг с другом. Например, в случае системы социальных связей, ребро между двумя вершинами будет означать, что два человека имеют связь друг с другом.
Шаг 3: Определение направленности ребер (необязательно)
В некоторых случаях может потребоваться указать направленность ребер графа. Например, если мы анализируем поток информации между различными вершинами, то можно указать направление этого потока.
После определения вершин и ребер графа, необходимо визуализировать его. Граф можно представить с помощью специальных программ или рисовать вручную. Для наглядности можно использовать различные стили и цвета, чтобы выделить определенные связи или группы вершин.
Шаг 5: Анализ графа
Построенный реберный граф можно использовать для анализа различных связей или паттернов. Например, можно исследовать центральные вершины, наиболее связанные вершины или группы вершин, которые обладают особыми свойствами.
В данном разделе мы рассмотрели основные шаги по построению реберного графа. Этот инструмент может быть полезен для анализа различных систем и сетей, а также помогает визуализировать сложные связи между элементами.
Примеры построения реберных графов
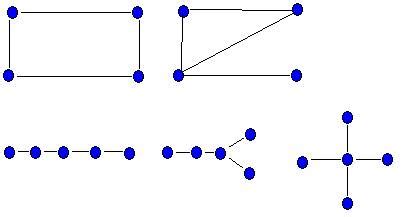
Пример 1:
Допустим, у нас есть исходный граф с вершинами A, B, C, D и ребрами AB, AC, BC, BD. Чтобы построить его реберный граф, мы добавляем вершины, соответствующие каждому ребру, а затем проводим ребра между вершинами, соответствующими ребрам, которые имеют общий конец. В данном случае ребра AB и AC имеют общий конец A, поэтому мы проводим ребро между вершинами AB и AC.
Пример 2:
Рассмотрим исходный граф с вершинами A, B, C и ребрами AB, AC, BC. Для построения реберного графа, мы добавляем вершины, соответствующие каждому ребру, и проводим ребра между вершинами, имеющими общий конец. В данном случае ребра AB и AC имеют общий конец A, поэтому мы проводим ребра между вершинами AB и AC. Ребро BC имеет общий конец C с ребром AC, поэтому мы проводим ребро между вершинами BC и AC.
Пример 3:
Предположим, у нас есть исходный граф с вершинами A, B, C и ребрами AB, AC, BC. Для создания реберного графа мы добавляем вершины, соответствующие каждому ребру, и соединяем их ребрами, имеющими общий конец. В данном примере ребра AB и AC имеют общий конец A, поэтому мы проводим ребра между вершинами AB и AC. Ребра BC и AC имеют общий конец C, поэтому мы проводим ребра между вершинами BC и AC.
Это лишь несколько примеров построения реберных графов. В зависимости от постановки задачи и характеристик исходного графа, построение реберного графа может варьироваться. Однако, основной принцип состоит в том, чтобы добавить вершины, соответствующие ребрам исходного графа, и провести ребра между вершинами, имеющими общий конец.
Важные моменты при построении реберного графа
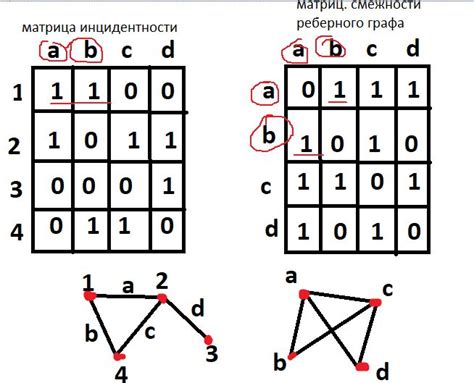
При построении реберного графа есть несколько важных моментов, которые следует учитывать. Эти моменты помогут сделать граф информативным, понятным и эффективным в использовании.
1. Выбор подходящей структуры
Первым шагом при построении реберного графа является выбор подходящей структуры данных для хранения графа. В зависимости от конкретной задачи и требований, можно использовать различные структуры, такие как списки смежности или матрицы смежности. Каждая структура имеет свои преимущества и недостатки, которые следует учитывать при выборе.
2. Определение вершин и ребер
Для построения реберного графа необходимо четко определить множество вершин и множество ребер. Вершины представляют объекты или сущности, между которыми могут быть установлены связи. Ребра представляют собой сами связи между вершинами. Важно определить, какие связи следует учитывать и какие вершины рассматривать в графе.
3. Установление взаимосвязей
Чтобы граф был информативным, необходимо установить правильные взаимосвязи между вершинами. Это поможет отразить основные связи и зависимости между объектами. Важно учитывать различные типы связей, такие как направленные и ненаправленные ребра, и выбирать соответствующие между ними типы связей.
4. Правильное обозначение ребер
При обозначении ребер в графе следует выбирать удобные и информативные метки. Это поможет легко понять основную суть ребра и его значимость в графе. Рекомендуется использовать понятные и краткие обозначения, которые будут понятны для всех пользователей.
5. Отображение графа
Учитывая эти важные моменты, построение реберного графа станет более эффективным и удобным. Следуя принципам хорошего проектирования, можно создать информативный и наглядный граф, который поможет лучше понять и анализировать взаимосвязи между объектами в заданной системе или предметной области.
Инструкция по построению реберного графа
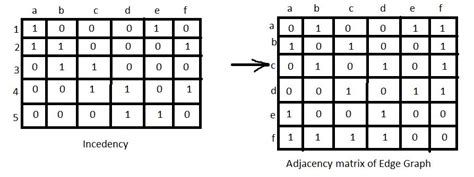
Шаг 1: Определение узлов
Первым шагом в построении реберного графа является определение всех узлов, которые будут представлены в графе. Узлы представляют собой объекты или сущности, между которыми могут существовать связи. Каждому узлу присваивается уникальное имя или метка.
Шаг 2: Определение связей
Затем необходимо определить связи между узлами. Связи могут быть направленными или ненаправленными, в зависимости от возможности двухстороннего взаимодействия между узлами. Каждая связь должна быть названа исходя из смысла их связи.
Шаг 3: Построение графа
Далее следует построение реберного графа с использованием определенных узлов и связей. Граф может быть представлен в виде диаграммы или матрицы, в зависимости от предпочтения и нужд анализа. Каждый узел изображается как точка или круг, а связи обозначаются линиями или стрелками, указывающими направление связи.
Шаг 4: Анализ графа
Последний шаг в построении реберного графа заключается в анализе полученного графа и выявлении особенностей его структуры. Можно определить наиболее центральные узлы, обнаружить наиболее интенсивные связи или выявить группы связанных узлов. Такой анализ может помочь в решении различных задач, таких как оптимизация связей или выявление слабых мест в структуре.
Построение реберного графа позволяет наглядно представить сложные структуры и взаимосвязи между их элементами. Этот инструмент является неотъемлемой частью анализа данных и позволяет выявлять особенности структуры, которые иначе могли бы быть упущены. Поэтому знание и умение построения реберного графа являются важными компетенциями в анализе и визуализации данных.