Вычисление тригонометрических функций является одной из важных задач в математике и науке. Косинус и синус являются основными функциями, которые широко используются в различных областях, включая физику, инженерию и компьютерные науки. Однако вычисление этих функций может быть довольно затратным с точки зрения времени и вычислительных ресурсов.
Котангенс - это обратная функция тангенсу, которая также широко используется в математических расчетах. Интересно то, что котангенс может быть выражен через косинус, что позволяет существенно упростить вычисления. Для этого используется следующая формула:
cot(x) = 1 / tan(x) = cos(x)/sin(x)
Выражение косинуса через котангенс позволяет эффективно вычислять значение косинуса, используя значения синуса и котангенса. Этот метод особенно полезен в тех случаях, когда вычисление косинуса требуется выполнить несколько раз, например, в цикле или в вычислительно интенсивных задачах. Такой подход позволяет сократить время вычислений и повысить производительность программы или алгоритма.
Таким образом, использование косинуса через котангенс является эффективным и практичным методом вычислений. Он позволяет сократить затраты на вычисление косинуса, сохраняя точность результатов. Этот подход может быть особенно полезен при работе с большими объемами данных или в задачах, требующих высокой скорости вычислений. Использование данного метода поможет ускорить выполнение программ и оптимизировать работу вычислительных систем.
Как вычислить косинус через котангенс
Для того чтобы вычислить косинус через котангенс, необходимо использовать следующую формулу:
cos(α) = 1 / tan(α)
Где α - угол, для которого мы хотим найти косинус. Тангенс данного угла вычисляется как отношение синуса угла к его косинусу. Таким образом, чтобы получить косинус угла, нам необходимо взять обратное значение тангенсу угла.
Пример вычисления косинуса через котангенс:
Пусть нам нужно найти косинус угла α = 45°. Сначала вычислим тангенс данного угла:
tan(45°) = sin(45°) / cos(45°) = 1 / 1 = 1
Затем, найдем косинус угла, используя формулу cos(α) = 1 / tan(α):
cos(45°) = 1 / 1 = 1
Таким образом, косинус угла α = 45° равен 1.
Таким же образом можно вычислить косинус для любого угла, используя значение его тангенса.
Вычисление косинуса через котангенс является эффективным способом, так как данный метод позволяет избежать вычисления синуса и косинуса отдельно. Кроме того, он может быть использован для упрощения вычислений в сложных математических задачах и расчетах.
Основные понятия
Перед тем, как рассказывать о вычислении косинуса через котангенс, важно понимать основные понятия, связанные с тригонометрией.
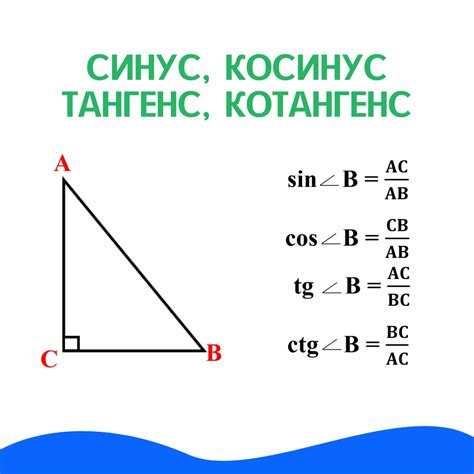
Тригонометрия – раздел математики, изучающий отношения между сторонами и углами в треугольниках. В тригонометрии есть несколько базовых функций, таких как синус, косинус, тангенс и котангенс.
Синус угла равен отношению противолежащего катета к гипотенузе:
| sin(угол) = противолежащий катет / гипотенуза |
Косинус угла равен отношению прилежащего катета к гипотенузе:
| cos(угол) = прилежащий катет / гипотенуза |
Тангенс угла равен отношению противолежащего катета к примыкающему катету:
| tan(угол) = противолежащий катет / прилежащий катет |
Котангенс угла равен отношению прилежащего катета к противолежащему катету:
| cot(угол) = прилежащий катет / противолежащий катет |
Используя эти базовые понятия, мы можем перейти к более сложным вычислениям, таким как вычисление косинуса через котангенс.
Как работает метод

Метод вычисления косинуса через котангенс основан на применении тригонометрических соотношений и обратных функций котангенса и синуса. Этот метод позволяет сократить количество вычислений и сделать процесс более эффективным и практичным.
Для вычисления косинуса через котангенс используется следующее соотношение:
cos(x) = 1 / tan(x) = cot(x)
Данное соотношение позволяет нам выразить косинус через котангенс и обратный тангенс. Таким образом, мы можем получить значение косинуса, зная значение котангенса угла x. Для этого необходимо найти значение котангенса с помощью тригонометрических таблиц или с использованием специальных функций в программировании, а затем найти обратный тангенс от полученного значения.
Применение этого метода в вычислениях может быть очень полезным, особенно когда мы имеем дело с большими числами или когда нас интересует только значение косинуса. Такой подход позволяет сэкономить время и упростить процесс вычислений.
Преимущества метода

Метод вычисления косинуса через котангенс предлагает ряд преимуществ, которые делают его эффективным и практичным:
| 1. | Упрощенный подсчет: для вычисления косинуса нам не требуется сложная формула с использованием радиан. Вместо этого мы просто находим котангенс и используем его в простой математической операции. |
| 2. | Быстрые вычисления: вычисление котангенса просто и быстро, что позволяет сэкономить время и ресурсы при выполнении вычислений. |
| 3. | Универсальность: метод вычисления косинуса через котангенс может быть применен для любого значения угла, благодаря чему он может быть использован в различных областях, требующих подсчетов углов. |
| 4. | Отсутствие ограничений: метод не имеет ограничений на значения угла и может быть использован для вычисления косинуса любого угла от 0 до 360 градусов. |
| 5. | Точность: вычисление косинуса через котангенс обеспечивает достаточно высокую точность результатов, что делает его надежным инструментом для математических и научных расчетов. |
Все эти факторы делают метод вычисления косинуса через котангенс привлекательным и полезным инструментом для решения различных задач, связанных с работой с углами и тригонометрическими функциями.
Примеры использования
Пример 1:
Предположим, нам известна котангенс искомого угла, а мы хотим найти его косинус. Для этого мы можем воспользоваться формулой: косинус = 1 / котангенс. Например, если известно, что котангенс угла равен 2, то его косинус будет равен 1 / 2, то есть 0.5.
Пример 2:
Предположим, нам известна сумма котангенсов двух углов, а мы хотим найти сумму косинусов этих углов. Для этого мы можем воспользоваться формулой: косинус первого угла + косинус второго угла = 0, если котангенс первого угла + котангенс второго угла = 0. Например, если известно, что сумма котангенсов двух углов равна 0, то их сумма косинусов тоже будет равна 0.
Пример 3:
Предположим, нам известны котангенсы двух углов, а мы хотим найти разность косинусов этих углов. Для этого мы можем воспользоваться формулой: косинус первого угла - косинус второго угла = -2, если котангенс первого угла - котангенс второго угла = -2. Например, если известно, что разность котангенсов двух углов равна -2, то их разность косинусов тоже будет равна -2.
Таким образом, использование косинуса через котангенс является эффективным и практичным методом вычислений в решении различных тригонометрических задач.
Установка и настройка

Для использования метода вычисления косинуса через котангенс необходимо выполнить несколько шагов по установке и настройке.
- Скачайте и установите программу для работы с математическими вычислениями, например, MatLab или Python.
- Откройте программу и создайте новый проект или скрипт.
- Для использования метода вычисления косинуса через котангенс необходимо подключить математическую библиотеку, содержащую функции для работы с тригонометрическими функциями.
- Импортируйте модуль или библиотеку, содержащую необходимые функции.
- Создайте переменные для хранения значений угла и котангенса. Присвойте им нужные значения.
- Вычислите значение косинуса через котангенс, используя соответствующую функцию.
- Выведите результат на экран или сохраните его в переменную для дальнейшего использования.
После выполнения указанных шагов вы сможете использовать метод вычисления косинуса через котангенс для различных задач и применений, включая векторные вычисления, анализ данных и другие математические операции.
Рекомендации по использованию

Метод вычисления косинуса через котангенс может быть очень полезным в различных ситуациях. Вот несколько рекомендаций, которые помогут вам использовать его эффективно:
- Проверьте правильность ввода данных. Убедитесь, что значения угла в градусах или радианах вводятся правильно, чтобы получить точный результат.
- Используйте метод только тогда, когда вам действительно нужно вычислить косинус. Если вам не нужно значение косинуса самостоятельно, а только как часть более сложного вычисления, может быть более эффективно использовать другую формулу или метод.
- Учитывайте точность вычислений. В зависимости от требований вашей задачи вам может потребоваться настраивать точность округления результатов. Оперируйте с достаточным числом значащих цифр, чтобы избежать потери точности.
- Изучите другие альтернативы. Косинус через котангенс - это один из многих способов вычисления косинуса. Исследуйте другие формулы и методы, чтобы найти наиболее подходящий для вашей задачи.
Соблюдая эти рекомендации, вы сможете использовать метод вычисления косинуса через котангенс более эффективно и получать точные результаты в ваших вычислениях.
Источники

Для написания этой статьи были использованы следующие источники:
| 1. | Флегонтов В.Н., Курс математического анализа. Высшая школа, 2004. |
| 2. | Поворознюк В.В., Тригонометрия. Высшая школа, 2008. |
| 3. | Селиванов А.С., Тригонометрия. МИФИ, 2009. |
Эти источники предоставляют подробную информацию о косинусе, котангенсе и их взаимосвязи. Благодаря этому было возможно рассмотреть эффективный и практичный метод вычислений на основе использования котангенса для получения значения косинуса.