Косинус параллелограмма является одной из основных тригонометрических функций, которая широко применяется в геометрии и физике. Она позволяет определить угол между двумя сторонами параллелограмма, а также вычислить длину этих сторон. Кроме того, косинус параллелограмма имеет ряд важных свойств и правил, которые помогают упростить его вычисление и применение в практических задачах. Давайте рассмотрим основные правила вычисления косинуса параллелограмма.
Для начала необходимо понять, что такое параллелограмм. Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны по длине. Он состоит из двух параллельных сторон и двух параллельных диагоналей, которые пересекаются в точке O. Угол между параллельными сторонами параллелограмма называется углом параллелограмма, и именно его мы будем вычислять с помощью косинуса параллелограмма.
Для вычисления косинуса параллелограмма применяются следующие правила. Пусть угол параллелограмма равен α, и стороны параллелограмма равны a и b. Тогда справедливы следующие формулы:
Косинус параллелограмма: cos(α) = a * b / (|a| * |b|),
Длина стороны параллелограмма: a = |a| = √(x1 - x2)² + (y1 - y2)²,
Длина диагонали параллелограмма: d = √(x1 - x3)² + (y1 - y3)².
Таким образом, зная значение угла параллелограмма и длины его сторон, мы можем вычислить косинус этого угла и другие геометрические параметры фигуры. Косинус параллелограмма является важной тригонометрической функцией, которая применяется во многих областях знаний и наук, включая физику, геометрию, математику и механику.
Косинус параллелограмма: основные правила вычисления
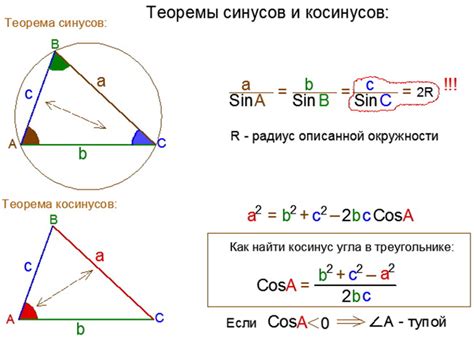
Для вычисления косинуса параллелограмма необходимо знать длины векторов, определяющих его стороны. Пусть A и B – два таких вектора. Тогда косинус параллелограмма может быть вычислен по формуле:
cos φ = (A·B) / (|A|·|B|)
где φ – угол между векторами A и B, А·B – скалярное произведение векторов, |A| и |B| – длины векторов A и B соответственно.
Важно отметить, что косинус параллелограмма принимает значения от -1 до 1. Значение 1 соответствует полной параллельности векторов A и B, а -1 – полной антипараллельности. Значение 0 означает, что векторы A и B перпендикулярны друг другу.
Вычисление косинуса параллелограмма позволяет определить силу связи между двумя векторами, а также позволяет решать различные задачи в геометрии, физике и других науках. Векторный анализ и геометрия параллелограмма – это основа для изучения многих сложных математических моделей и применение их в практических задачах.
Значение косинуса параллелограмма
| Величина | Формула |
|---|---|
| Косинус параллелограмма | cos(α) = (a^2 + b^2 - c^2) / (2 * a * b) |
Где α - угол между сторонами параллелограмма, a и b - длины этих сторон, c - длина диагонали параллелограмма.
Значение косинуса параллелограмма может иметь значения от -1 до 1. Если косинус равен 1, то угол α равен 0 градусов и стороны параллелограмма совпадают. Если косинус равен -1, то угол α равен 180 градусов и стороны параллелограмма противоположны друг другу. Когда косинус равен 0, угол α равен 90 градусов и стороны параллелограмма перпендикулярны друг другу.
Зная значение косинуса параллелограмма и длины сторон, можно вычислить углы этого фигуры и находить другие связанные параметры.
Вычисление косинуса параллелограмма с помощью длин векторов
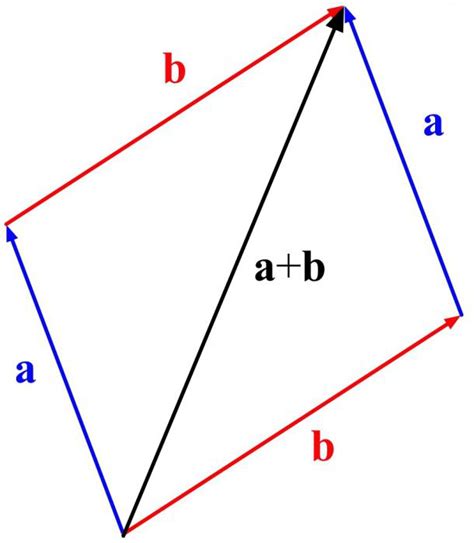
Косинус параллелограмма может быть вычислен с использованием длин векторов, которые представляют его стороны. Для того чтобы вычислить косинус параллелограмма, необходимо знать длины его сторон и угол между ними.
Пусть у нас есть параллелограмм ABCD, где AB и AD являются его сторонами, a и b - их длины, а угол между ними обозначается как α. Косинус параллелограмма вычисляется по формуле:
cos(α) = (AB^2 + AD^2 - BD^2) / (2 * a * b), где AB^2 обозначает квадрат длины стороны AB, AD^2 - квадрат длины стороны AD, а BD^2 - квадрат длины диагонали BD.
Подставив известные значения в формулу, мы можем вычислить значение косинуса параллелограмма.
Например, если AB = 5, AD = 8, и угол α между ними равен 60 градусам, мы можем вычислить косинус параллелограмма BCDA следующим образом:
AB^2 = 5^2 = 25
AD^2 = 8^2 = 64
BD^2 = AB^2 + AD^2 - 2 * AB * AD * cos(α)
BD^2 = 25 + 64 - 2 * 5 * 8 * cos(60) = 25 + 64 - 80 = 9
cos(α) = (AB^2 + AD^2 - BD^2) / (2 * a * b)
cos(α) = (25 + 64 - 9) / (2 * 5 * 8) = 80 / 80 = 1
Таким образом, косинус параллелограмма BCDA равен 1.
Применение формулы косинуса параллелограмма в практике
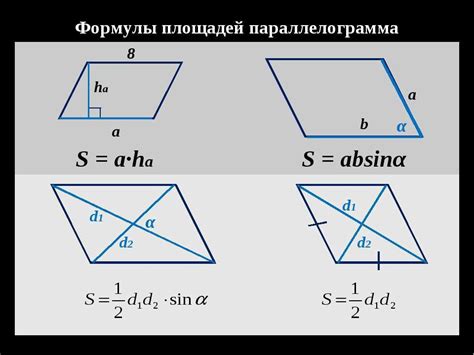
Одной из основных задач, которую можно решить с помощью косинуса параллелограмма, является вычисление площади фигуры. По определению, площадь параллелограмма равна произведению длин двух его смежных сторон на синус угла между ними. Однако, с помощью формулы косинуса можно переписать эту формулу и определить площадь параллелограмма через длины двух смежных сторон и угол между ними.
Другой важной задачей, которую можно решить с использованием косинуса параллелограмма, является определение длины третьей стороны фигуры. Если известны длины двух смежных сторон и угол между ними, то по формуле косинуса можно вычислить значение третьей стороны параллелограмма.
Кроме того, формула косинуса параллелограмма может быть использована для определения углов фигуры. Если известны длины трех смежных сторон, то с помощью косинуса можно вычислить значения углов параллелограмма. Это особенно полезно при решении геометрических задач и построении фигур.
Таким образом, формула косинуса параллелограмма имеет множество практических применений, помогая решать задачи, связанные с вычислением площади, длины сторон и углов этой геометрической фигуры. Знание и использование этой формулы позволяет упростить решение задач и облегчить работу с параллелограммами.
Свойства и особенности косинуса параллелограмма
1. Определение:
Косинус параллелограмма – это тригонометрическая функция, которая позволяет определить угол между двумя сторонами этого параллелограмма.
2. Формула вычисления:
Косинус параллелограмма вычисляется по формуле:
cos α = (AB · BC) / (|AB| · |BC|)
Где:
- α – угол между сторонами AB и BC
- AB и BC – стороны параллелограмма
- |AB| и |BC| – длины соответствующих сторон
- · обозначает векторное произведение
3. Свойства:
Косинус параллелограмма обладает следующими свойствами:
- Значение косинуса параллелограмма лежит в интервале [-1, 1].
- Косинус параллелограмма равен 1, если угол α равен 0°, т.е. стороны AB и BC лежат на одной прямой.
- Косинус параллелограмма равен -1, если угол α равен 180°, т.е. стороны AB и BC лежат на противоположных прямых.
- Косинус параллелограмма равен 0, если стороны AB и BC перпендикулярны друг другу, т.е. угол α равен 90°.
- Если угол α прямой, то косинус параллелограмма равен 0.
- Косинус параллелограмма имеет периодическую зависимость с периодом 360°.
4. Важное замечание:
Если векторы AB и BC не являются сторонами параллелограмма, то вычисление косинуса параллелограмма некорректно. В данном случае следует использовать другие методы вычисления углов или длин сторон.