В геометрии существует много разных понятий и формул, которые помогают нам изучать и анализировать фигуры и объекты. Одной из таких формул является формула косинуса, которая находит свое применение в треугольниках. Косинус треугольника – это одно из основных геометрических понятий, которое помогает нам определить отношение между сторонами и углами треугольника.
Косинус треугольника определяется соотношением между длиной одной стороны треугольника и углом, образованным этой стороной и другими двумя сторонами. Формула косинуса выглядит следующим образом: cos(A) = (b^2 + c^2 - a^2) / (2 * b * c), где A – угол, b и c – стороны треугольника.
Косинус треугольника имеет множество практических применений в различных областях. Например, его используют для изучения физики и механики, а также в решении задач связанных с тригонометрией. Косинус треугольника позволяет нам вычислить углы и стороны треугольника, а также определить его форму и свойства. Это необходимо, например, при построении и изучении геометрических фигур или в решении задач на геометрическую оптику и межпланетную навигацию.
Что такое косинус треугольника и как его вычислить?
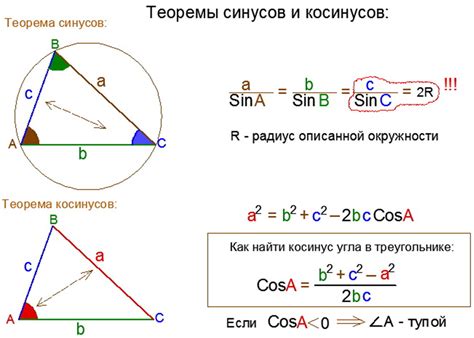
Для вычисления косинуса треугольника используется следующая формула:
- cos(A) = b / c, где A – угол между гипотенузой и одной из сторон, b – длина этой стороны, c – длина гипотенузы.
Существует несколько способов вычисления косинуса треугольника. Если известны длины всех сторон треугольника, можно воспользоваться формулой косинусов:
- cos(A) = (b^2 + c^2 - a^2) / (2 * b * c), где A – угол между сторонами b и c, a – длина третьей стороны.
Если известны длины двух сторон треугольника и величина между ними угла, то можно воспользоваться формулой косинусов:
- cos(A) = (b^2 + c^2 - a^2) / (2 * b * c), где A – угол между сторонами b и c, a – длина третьей стороны.
Косинус треугольника имеет широкое практическое применение. Он может использоваться для нахождения неизвестных сторон и углов треугольника, для определения подобия треугольников, для рассчета площади треугольника и многих других геометрических задач.
Как работает формула косинуса треугольника?
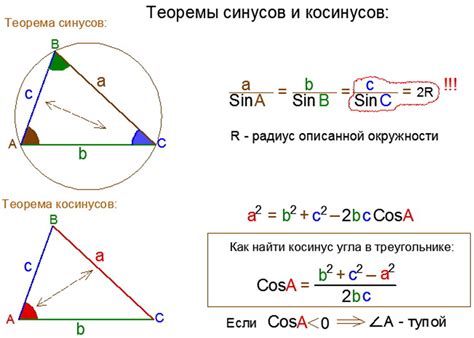
Формула косинуса треугольника используется для вычисления значения косинуса угла внутри треугольника. Косинус это отношение длины прилегающего катета к гипотенузе треугольника. Формула выражается следующим образом:
cos(α) = a / c
где α - угол внутри треугольника, a - прилегающий катет, c - гипотенуза треугольника
Данная формула основывается на теореме Пифагора, которая утверждает, что квадрат гипотенузы треугольника равен сумме квадратов двух катетов.
Практическое применение формулы косинуса треугольника включает в себя решение задач геометрии и тригонометрии. Например, с помощью формулы можно вычислить длину стороны треугольника, если известны значения двух других сторон и угла между ними.
Для использования формулы косинуса треугольника достаточно знать значения двух сторон и угла между ними. После подстановки этих значений в формулу можно получить значение косинуса угла и использовать его в решении задачи.
Как вычислить косинус треугольника по длинам его сторон?
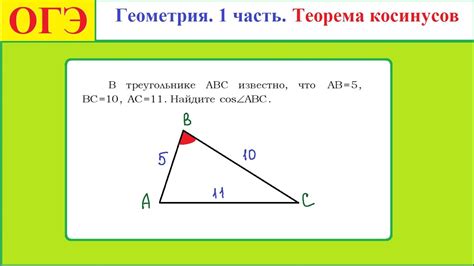
Для вычисления косинуса треугольника по длинам его сторон можно воспользоваться формулой косинуса, которая выглядит следующим образом:
| Формула косинуса треугольника | ||
|---|---|---|
| cos(A) = (b^2 + c^2 - a^2) / (2 * b * c) | cos(B) = (a^2 + c^2 - b^2) / (2 * a * c) | cos(C) = (a^2 + b^2 - c^2) / (2 * a * b) |
Где А, В и С - углы треугольника, а a, b и c - длины его сторон.
Чтобы вычислить косинус треугольника по длинам его сторон, необходимо знать длины всех трех сторон. Подставив значения в формулу, можно определить косинус каждого угла треугольника.
Зная косинусы углов треугольника, можно рассчитать дополнительные характеристики, такие как площадь, периметр, радиусы вписанной и описанной окружностей и т.д. Косинус также используется в различных областях, таких как геодезия, физика и графика.
Практическое применение косинуса треугольника

1. Решение треугольников
Косинус треугольника позволяет нам решать различные задачи, связанные с тригонометрией. Например, если известны длины двух сторон треугольника и угол между ними, то с помощью косинуса треугольника можно вычислить длину третьей стороны. Это может быть полезно, например, при создании конструкций или проектировании объектов.
2. Навигация и картография
Косинус треугольника используется для определения расстояний и направлений на карте или местности. Если у нас есть информация о позиции двух точек на земле (широта, долгота) и угле между ними, то с помощью косинуса треугольника можно вычислить расстояние и направление между этими точками. Это особенно важно для мореплавания, авиации и спутниковой навигации.
3. Физика
Косинус треугольника широко используется в физике, особенно при изучении сил и векторов. Например, при вычислении компонентов силы по направлению и углу наклона, угол между силой и горизонтом может быть выражен с помощью косинуса треугольника. Это помогает установить, какая часть силы направлена по горизонтали и вертикали.
Важно помнить, что для получения точных результатов необходимо использовать единицы измерения, соответствующие задаче, и учитывать особенности треугольника и углов, с которыми вы работаете.
Таким образом, косинус треугольника играет важную роль в геометрии и находит свое применение в решении различных задач. Понимание его принципов и использование позволяют нам решать сложные задачи и применять знания тригонометрии на практике.
Расчет высоты треугольника с использованием косинуса
h = a * cos(theta)
где h - высота треугольника, a - длина стороны, примыкающей к углу theta.
Данная формула позволяет рассчитать высоту треугольника при известных значениях его стороны и угла при этой стороне. Расчет высоты треугольника с использованием косинуса может быть полезен для решения различных задач, например:
- Определение высоты горы или дерева на основе известного угла и расстояния до объекта;
- Определение высоты здания по измеренному углу наклона и расстоянию до здания;
- Расчет высоты паруса на яхте на основе известного угла между парусом и горизонтом;
- Определение высоты объектов на фотографии после проведения поправки на перспективу.
Таким образом, косинус треугольника является полезным математическим инструментом для решения задач в различных областях, связанных с геометрией и измерениями высоты.
Определение угла между сторонами треугольника с помощью косинуса
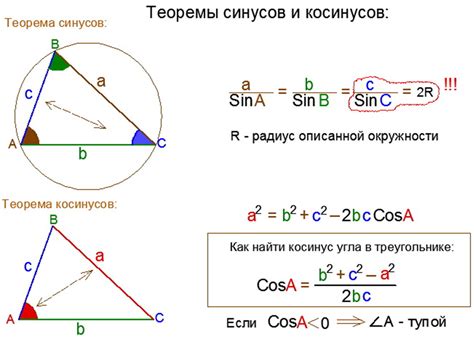
cos(𝐴) = (𝑏² + 𝑐² − 𝑎²) / (2𝑏𝑐)
cos(𝐵) = (𝑎² + 𝑐² − 𝑏²) / (2𝑎𝑐)
cos(𝐶) = (𝑎² + 𝑏² − 𝑐²) / (2𝑎𝑏)
В этих формулах 𝐴, 𝐵 и 𝐶 - это углы треугольника, а 𝑎, 𝑏 и 𝑐 - длины его сторон.
Выражение в числителе формулы представляет собой сумму квадратов двух сторон треугольника, вычитаемую из квадрата третьей стороны. Затем полученное значение делится на произведение длин двух сторон, соединяющих данный угол.
Используя формулу косинуса, можно определить значение трех углов треугольника. Зная длины сторон, можно вычислить каждый угол, подставив соответствующие значения в формулу.
Практическое применение косинуса треугольника заключается в решении геометрических задач, измерении углов и определении соотношений между сторонами треугольника. Косинус треугольника может быть полезен при проектировании зданий, строительстве дорог, навигации и многих других отраслях математики, физики и инженерии.