Косинус – это одна из основных тригонометрических функций, которая широко применяется в математике и ее приложениях. Он особенно полезен при решении задач связанных с геометрией, таких как вычисление расстояния между точками или нахождение углов между векторами. Косинус треугольника является важной составляющей в этих вычислениях и определяет отношение длины катета к гипотенузе.
Формула косинуса треугольника основывается на теореме Пифагора и утверждает, что для любого прямоугольного треугольника выполняется следующее соотношение: квадрат длины гипотенузы равен сумме квадратов длин катетов. Используя эту формулу, мы можем вычислить значения косинуса для каждого угла треугольника.
Существует несколько способов вычисления косинуса треугольника. Один из самых простых способов - использовать величины всех сторон треугольника. Для этого необходимо найти значения всех сторон треугольника и затем применить формулу косинуса, указывая эти значения. Другой способ заключается в использовании координатных осей и знания точных координат вершин треугольника. При помощи этих данных мы можем применить формулу косинуса, чтобы определить значения косинуса углов.
Значение и применение косинуса треугольника
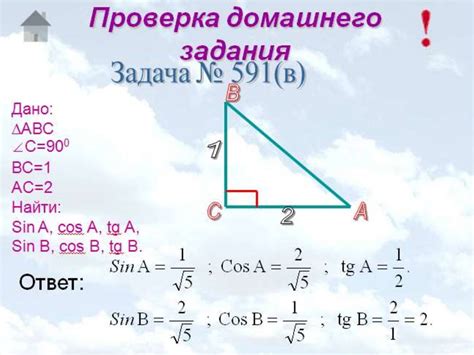
Косинус треугольника имеет множество применений в различных областях науки и техники. Одно из основных применений - решение задачи нахождения неизвестной стороны треугольника при известных значениях других сторон и углов.
Другое важное применение косинуса треугольника - нахождение углов треугольника по известным значениям его сторон. Для этого можно использовать обратную функцию косинуса - арккосинус.
Косинус треугольника также используется в геометрии при определении прямолинейного движения по известным значениям скорости и угла движения.
Кроме того, косинус треугольника находит свое применение в физике, при изучении динамики движения объектов под воздействием силы тяжести или других сил.
Знание формулы и способа вычисления косинуса треугольника позволяет решать различные задачи, связанные с геометрией, физикой, инженерией, а также использовать его в программировании и математическом моделировании.
Формула и определение
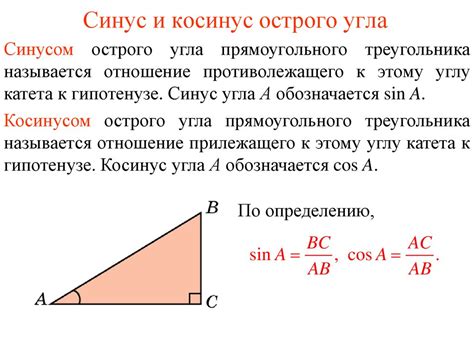
Формула для вычисления косинуса треугольника основана на теореме Пифагора и выражается следующим образом:
cos(A) = adjacent / hypotenuse
где:
- cos(A) - косинус угла A;
- adjacent - длина прилегающего катета;
- hypotenuse - длина гипотенузы.
Таким образом, косинус треугольника позволяет определить отношение длин сторон треугольника и угла между ними. Эта функция широко используется в геометрии, физике и других науках при решении различных задач.
Способы вычисления косинуса треугольника

| Метод | Формула |
|---|---|
| 1. Используя длины сторон треугольника | cos(A) = (b^2 + c^2 - a^2) / (2bc) |
| 2. Используя значения углов треугольника | cos(A) = cos(a) = (b^2 + c^2 - a^2) / (2bc) |
| 3. Используя координаты вершин треугольника | cos(A) = (AB · AC) / (|AB| * |AC|) |
Выбор способа вычисления косинуса треугольника зависит от имеющихся данных и требуемой точности. Важно помнить, что косинус треугольника может быть вычислен только для остроугольных треугольников. Если треугольник является тупоугольным, то косинус тупого угла будет отрицательным.