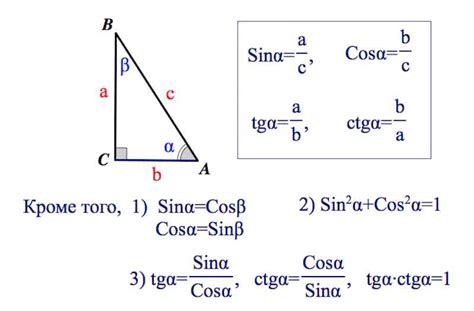
Косинус и синус являются фундаментальными тригонометрическими функциями, которые широко используются в математике, физике и других науках. Изучение связи между этими функциями позволяет решать разнообразные задачи, включая определение неизвестных углов и расчет длин сторон треугольников.
Формула, связывающая косинус и синус угла, известна как формула косинуса. Она устанавливает, что квадрат косинуса угла равен разности единицы и квадрата синуса этого же угла. Математически эта формула записывается как:
cos2(α) = 1 - sin2(α)
Используя данную формулу, можно рассчитать значение косинуса угла, если известно значение синуса этого угла. Для этого необходимо возвести синус угла в квадрат, вычесть полученное значение из единицы и извлечь квадратный корень из полученного результата. Полученное число будет являться косинусом исходного угла.
Понимание формулы косинуса и синуса, а также умение применять их в практических расчетах, позволяет решать различные задачи, связанные с треугольниками, углами и геометрическими фигурами. Эти навыки находят применение в таких областях, как геодезия, астрономия, физика и инженерное дело.
Какой косинус угла по формуле синуса?

Формула для нахождения косинуса угла по синусу выглядит следующим образом:
cos(α) = ±√(1 - sin²(α))
Знак ± указывает на то, что значение косинуса может быть положительным или отрицательным, в зависимости от значений катетов и гипотенузы треугольника.
Для вычисления косинуса угла по формуле синуса сначала нужно найти значение синуса угла, а затем подставить его в формулу и выполнить вычисления. Полученный результат будет являться значением косинуса угла.
Зная формулу для косинуса по синусу, мы можем легко расчитать значения косинуса угла, используя графики или таблицы значений синусов и косинусов.
Например, если синус α = 0.8, то соответствующий косинус можно расчитать следующим образом:
cos(α) = ±√(1 - sin²(α))
cos(α) = ±√(1 - 0.8²)
cos(α) = ±√(1 - 0.64)
cos(α) = ±√(0.36)
cos(α) ≈ ±0.6
Таким образом, косинус угла α, если синус α равен 0.8, будет примерно равняться ±0.6.
Вычисление косинуса угла через синус
Один из таких способов - использование тригонометрической формулы:
cos(α) = √(1 - sin^2(α)),
где α - угол, sin(α) - синус угла α.
Для вычисления косинуса угла через синус необходимо сначала найти квадрат синуса угла, затем вычесть его из 1 и извлечь квадратный корень от полученного значения.
Например, если sin(α) = 0.6, то положим этот результат в формулу:
cos(α) = √(1 - 0.6^2) = √(1 - 0.36) = √0.64 = 0.8.
Таким образом, косинус угла α, где sin(α) = 0.6, равен 0.8.
Это лишь один из способов вычисления косинуса угла, но он является одним из наиболее распространенных и простых для понимания.
Формула для расчета косинуса угла по синусу
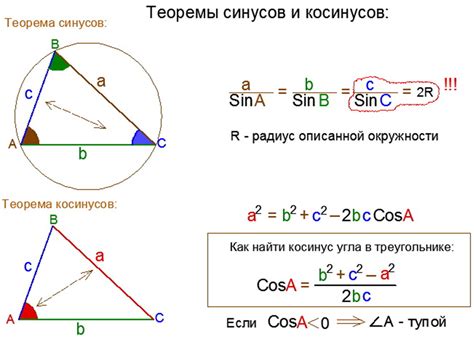
Формула для расчета косинуса угла по синусу выглядит следующим образом:
cos(угол) = ±√(1 - sin^2(угол))
В этой формуле "угол" представляет собой значение угла в радианах или градусах. Знак ± указывает на то, что косинус может быть положительным или отрицательным, в зависимости от квадранта, в котором находится угол.
Чтобы рассчитать косинус угла по его синусу, следует сначала возвести значение синуса угла в квадрат, затем вычесть это значение из единицы и взять квадратный корень из получившегося результата.
Например, если дан угол, чей синус равен 0,6, чтобы найти его косинус, нужно выполнить следующие действия:
cos(угол) = ±√(1 - 0,6^2)
cos(угол) = ±√(1 - 0,36)
cos(угол) = ±√0,64
cos(угол) = ±0,8
Итак, косинус угла будет равен ±0,8.
Формула для расчета косинуса угла по синусу позволяет перейти от одной тригонометрической функции к другой и находит широкое применение в различных областях знаний.
Примеры расчетов косинуса угла
Пример 1:
Рассмотрим прямоугольный треугольник ABC, где угол С равен 60 градусов и гипотенуза AC равна 10 единиц. Для расчета косинуса угла С, мы можем использовать формулу:
косинус С = прилежащий катет / гипотенуза
В данном примере, прилежащий катет AC равен 10 * cos(60°) = 5 единиц.
Пример 2:
Предположим, что у нас есть угол D, равный 45 градусам, и катет AD, равный 8 единиц. Мы можем использовать формулу для расчета косинуса угла D:
косинус D = прилежащий катет / гипотенуза
Таким образом, косинус угла D равен 8 * cos(45°) = 8 * (sqrt(2) / 2) = 4 * sqrt(2) единиц.
Пример 3:
Допустим, у нас есть прямоугольный треугольник PQR, угол Q равен 30 градусам, гипотенуза PR равна 6 единиц, а прилежащий катет PQ равен 3 единицам. Для расчета косинуса угла Q, мы можем использовать формулу:
косинус Q = прилежащий катет / гипотенуза
В данном случае, косинус угла Q равен 3 / 6 = 0.5 единицы.
Это лишь несколько примеров расчета косинуса угла. Формула исключительно зависит от значений угла и длины сторон треугольника, поэтому расчет может быть произведен для любого треугольника с известными значениями.
Пример 1: Расчет косинуса угла по синусу
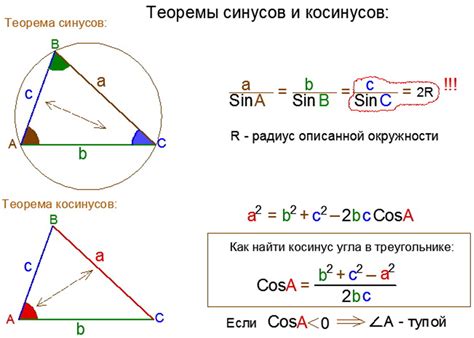
Чтобы рассчитать косинус угла по его синусу, необходимо использовать тригонометрическую формулу:
cos Ɵ = √(1 - sin^2 Ɵ),
где Ɵ - угол, sin Ɵ - синус угла.
Давайте рассмотрим пример расчета косинуса угла по его синусу:
- Пусть у нас есть треугольник, в котором синус угла равен 0.8.
- Подставляем значение синуса в формулу: cos Ɵ = √(1 - sin^2 Ɵ).
- Выполняем вычисления: cos Ɵ = √(1 - 0.8^2) = √(1 - 0.64) = √0.36 = 0.6.
Таким образом, косинус угла, соответствующего синусу 0.8, равен 0.6.
Зная синус угла, вы можете использовать эту формулу для расчета косинуса и нахождения других значений, связанных с углом.
Пример 2: Как найти косинус угла через синус
Существует простая формула, позволяющая найти косинус угла, если известен синус этого угла. Для этого необходимо использовать тригонометрическое тождество:
косинус угла = √(1 - синус^2 угла)
Для примера, представим себе угол, у которого синус равен 0.6. Чтобы найти косинус этого угла, мы должны подставить значение синуса в формулу:
косинус угла = √(1 - 0.6^2) ≈ √(1 - 0.36) ≈ √0.64 ≈ 0.8
Таким образом, косинус угла равен примерно 0.8.
Теперь вы можете использовать эту формулу, чтобы быстро найти косинус угла через синус, не проводя сложных вычислений.
Применение формулы косинуса угла по синусу
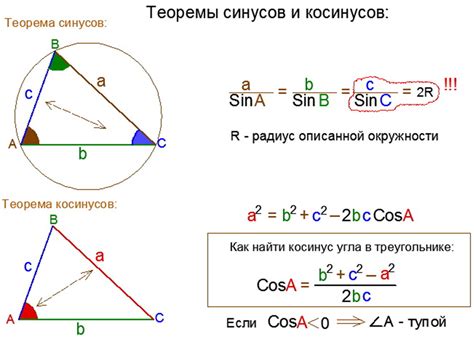
Формула косинуса угла по синусу позволяет вычислить значение косинуса угла, если известен синус этого угла и его ориентация на координатной плоскости.
Косинус угла по синусу вычисляется по следующей формуле:
cos(α) = ±√(1 - sin²(α))
Здесь α - угол, sin(α) - его синус.
Математическая формула позволяет найти значения косинуса угла в пределах от -1 до 1, но со знаком "±" отражает его ориентацию:
- Если sin(α) положительный и α лежит в первой или четвёртой четверти, то косинус α также положительный.
- Если sin(α) положительный и α лежит во второй или третьей четверти, то косинус α отрицательный.
- Если sin(α) равен нулю, то косинус α равен 1.
Формула косинуса угла по синусу широко применяется в различных областях, таких как геометрия, тригонометрия, физика, инженерия и другие, и используется для нахождения значений тригонометрических функций углов и решения разнообразных задач.
Вычисление косинуса угла с помощью формулы синуса
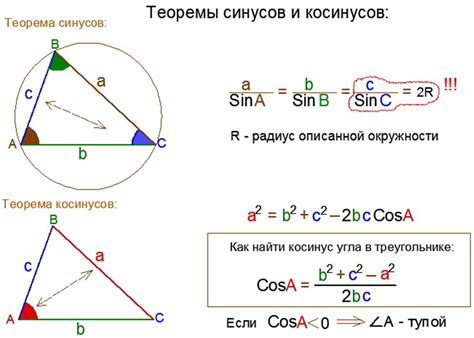
Формула для вычисления косинуса угла по синусу имеет следующий вид:
cos(α) = sqrt(1 - sin^2(α))
где α - угол, sin(α) - значение синуса угла.
Для вычисления косинуса угла нужно сначала получить значение синуса угла, а затем применить эту формулу. Например, если у нас есть угол α, для которого sin(α) равно 0.6, можно вычислить косинус угла следующим образом:
cos(α) = sqrt(1 - sin^2(α))
cos(α) = sqrt(1 - (0.6)^2)
cos(α) = sqrt(1 - 0.36)
cos(α) = sqrt(0.64)
cos(α) ≈ 0.8
Таким образом, косинус угла α при заданном значении синуса равен примерно 0.8.
Формула вычисления косинуса угла по синусу позволяет быстро и удобно определить значение этой тригонометрической функции без использования таблиц косинусов или специальных калькуляторов.
Значение косинуса угла при известном синусе

cos(α) = sqrt(1 - sin^2(α)),
где α - значение угла, sin(α) - синус угла.
Используя данную формулу, можно расчитать значение косинуса угла при известном синусе. Для этого нужно:
- Найти значение синуса угла, обратившись к таблицам или использовав соотношение с другими геометрическими параметрами.
- Возвести значение синуса угла в квадрат и вычесть из 1.
- Извлечь квадратный корень из полученного числа.
Таким образом, значение косинуса угла можно рассчитать, зная значение синуса. Например, если синус угла равен 0,5, то косинус угла будет равен sqrt(1 - 0,5^2) = sqrt(1 - 0,25) = sqrt(0,75) ≈ 0,866.
Значение косинуса угла при известном синусе имеет важное значение в тригонометрии, геометрии, физике и других областях науки.