Число Паскаля – это числовой треугольник, в котором каждый элемент получается путем сложения двух элементов, расположенных над ним. Это треугольник был впервые описан и назван в честь французского математика Блеза Паскаля. Главное свойство числа Паскаля – замечательная комбинаторная структура, показывающая связь между комбинаторными коэффициентами и алгеброй. Относительно изучения кратности суммы цифр двузначного числа трем в числах Паскаля, существует гипотеза.
Согласно этой гипотезе, сумма цифр двузначного числа будет кратна трем, если и только если это число находится на одном из боковых краев треугольника Паскаля. К примеру, числа 1, 10, 45, 120 и так далее, образуют края треугольника Паскаля и являются кратными трем.
Доказательство этой гипотезы требует дополнительных исследований и математических доказательств. Существуют различные методы и подходы для исследования свойств числа Паскаля, и каждый из них играет важную роль в понимании и применении этой комбинаторной конструкции. Исследования в области чисел Паскаля позволяют нам расширять границы нашего знания и открывать новые тайны комбинаторики и алгебры.
Кратность суммы цифр
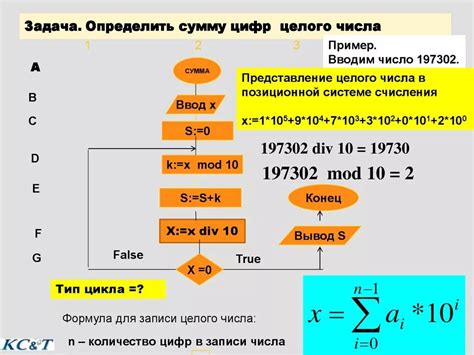
Чтобы понять кратность суммы цифр двузначного числа, сначала необходимо разложить число на цифры. Например, для числа 47 сумма цифр будет равна 4 + 7 = 11. Затем нужно определить, сколько раз сумма цифр делится на три. Если сумма цифр делится на три без остатка, то кратность будет равна 1. Если остаток от деления равен одному, то кратность будет равна 2. Если остаток равен двум, то кратность равна 0.
В числе Паскаля можно выделить специфические свойства кратности суммы цифр двузначных чисел. Например, сумма цифр любого числа Паскаля будет кратна трём числом, номер которого чётный. То есть, если в числе Паскаля цифр четное количество, то сумма цифр двузначных чисел будет кратна трем.
| Число Паскаля | Сумма цифр двузначного числа | Кратность суммы цифр трем |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 2 | 0 |
| 3 | 3 | 1 |
| 4 | 4 | 0 |
| 5 | 5 | 2 |
| 6 | 6 | 0 |
| 7 | 7 | 0 |
| 8 | 8 | 2 |
| 9 | 9 | 1 |
Двузначное число

Двузначное число представляет собой число, состоящее из двух цифр. Всего существует 90 двузначных чисел, начиная с 10 и заканчивая 99. Двузначные числа могут быть положительными, отрицательными или нулевыми, в зависимости от значения их цифр.
Двузначные числа удобно представлять в виде таблицы, где первая цифра представлена в столбце десятков, а вторая цифра - в столбце единиц. В таблице можно наблюдать, что двузначные числа увеличиваются от 10 до 99 последовательно, меняя только последнюю цифру.
| 10 | 11 | 12 | 13 | 14 | 15 | ... | 98 | 99 |
Каждое двузначное число можно представить в виде суммы десятков и единиц. Например, число 45 можно представить как 40 + 5. Важно отметить, что сумма цифр не может быть больше 18, так как самое большое двузначное число - 99.
В числе Паскаля можно найти двузначные числа, у которых сумма цифр кратна трем. Например, число 12 (1 + 2 = 3) и число 39 (3 + 9 = 12) удовлетворяют данному условию. Это связано с особенностями треугольника Паскаля, где каждое число представляет сумму двух чисел расположенных над ним.
Число Паскаля

В числе Паскаля второй строкой начинается ряд двузначных чисел, которые по сравнению со строкой выше образуют новые числа. Например, число 1 образуется путем сложения чисел 0 и 1 из предыдущей строки. Далее, 2 получается как сумма 1 и 1, 3 как сумма 1 и 2 и так далее.
Каждое число в числе Паскаля может быть представлено в биномиальной форме (a + b)^n, где a и b - элементы из предыдущей строки, а n - номер строки числа Паскаля. Например, третье число 3 в числе Паскаля может быть записано как (1 + 2)^3 = 27.
Изучение числа Паскаля позволяет исследовать свойства и закономерности, связанные с различными комбинаторными объектами, такими как сочетания, мультимножества, числа Белла и многое другое.