Квадрат - одна из самых простых и в то же время уникальных геометрических фигур. У каждого из нас в школьные годы был знаком этот стройный и симметричный параллелограмм, стороны которого образуют правые углы и равны между собой. Но действительно ли любой квадрат является параллелограммом?
Давайте разберемся. Параллелограмм - это геометрическая фигура, у которой противоположные стороны параллельны и равны между собой. Он обладает несколькими особенностями, которые делают его уникальным и привлекательным для изучения. Во-первых, в нем все стороны имеют одинаковую длину, что делает его симметричным и эстетичным. Во-вторых, его противоположные стороны параллельны и никогда не пересекаются, что позволяет рассматривать его как результат соединения двух параллельных линий. И, наконец, внутри параллелограмма противоположные углы равны между собой, а сумма всех его углов составляет 360 градусов.
Однако, не все квадраты могут считаться параллелограммами. Важно понимать, что хотя каждый квадрат обладает свойствами параллелограмма - противоположные стороны параллельны и равны, а также все углы правые, - не каждый параллелограмм может быть квадратом. Для того чтобы квадрат считался таковым, его стороны должны быть равными между собой, а углы - правыми. Это значит, что не все параллелограммы одновременно являются и квадратами, хотя все квадраты, несомненно, являются параллелограммами.
Квадрат: параллелограмм или нет?

Во-первых, все стороны квадрата равны между собой, что делает его структурой более специализированной, нежели классический параллелограмм.
Во-вторых, все углы квадрата являются прямыми, что отличает его от произвольного параллелограмма, где углы могут быть различными.
Таким образом, можно сказать, что каждый квадрат - это особый вид параллелограмма, который сочетает в себе все его характеристики, но с дополнительными условиями равных сторон и прямых углов.
Отметим, что не все параллелограммы являются квадратами, так как им необходимо удовлетворять дополнительным условиям равенства сторон и прямых углов.
Таким образом, можно заключить, что хотя квадрат является частным случаем параллелограмма, не все параллелограммы являются квадратами.
Определение и свойства

| Определение | Квадрат - это фигура, у которой все четыре стороны равны друг другу, а все углы прямые. |
| Стороны | У квадрата все стороны равны между собой. Обозначаются буквой a. |
| Углы | Все углы квадрата являются прямыми углами (90 градусов). |
| Площадь | Площадь квадрата вычисляется по формуле: S = a^2, где a - длина стороны. |
| Периметр | Периметр квадрата вычисляется по формуле: P = 4a, где a - длина стороны. |
| Диагонали | В квадрате существуют две равные диагонали, которые делят его на четыре равных треугольника. |
| Симметрия | Квадрат обладает симметрией относительно своих сторон, диагоналей и центра. |
Квадрат является простейшей и наиболее удобной для изучения геометрической фигурой. Его особенности и свойства широко применяются в математике, физике, архитектуре и других науках и отраслях деятельности.
Различия между квадратом и параллелограммом
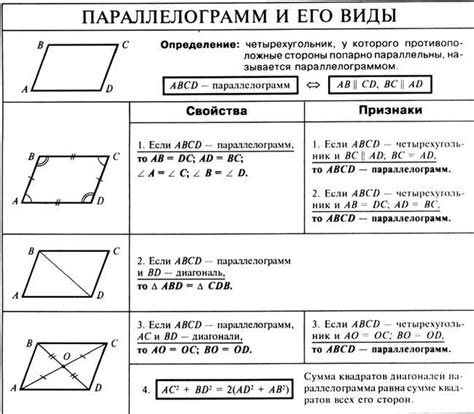
1. Стороны: У квадрата все четыре стороны равны друг другу, в отличие от параллелограмма, у которого только противоположные стороны равны.
2. Углы: У квадрата все углы прямые, то есть равны 90 градусам. В параллелограмме углы могут быть различными.
3. Диагонали: Диагонали квадрата равны друг другу и пересекаются в точке, делящей их пополам. В параллелограмме диагонали могут быть разными по длине и не пересекаться в точке, делящей их пополам.
4. Симметрия: Квадрат обладает симметрией относительно всех своих осей и диагоналей. Параллелограмм не обязательно обладает такой симметрией.
Таким образом, хотя квадрат является особой разновидностью параллелограмма, он имеет дополнительные характеристики, которые делают его уникальным и особенным в своем роде геометрическим объектом.
Основные характеристики геометрических фигур

Периметр - это длина внешней границы фигуры. Для круга нет периметра, вместо этого используется его аналогичная характеристика - длина окружности.
Площадь - это мера плоской поверхности, заключенной внутри фигуры. Площадь круга вычисляется по формуле S = π * r^2, где π - математическая константа, равная примерно 3,14159, а r - радиус окружности.
Прямоугольник - это частный случай параллелограмма, у которого все углы прямые (90°). Его площадь вычисляется по формуле S = a * b, где a и b - длины сторон прямоугольника.
Треугольник - это фигура, у которой три стороны и три угла. Площадь треугольника можно найти, используя различные методы, например, формулу Герона: S = √(p * (p - a) * (p - b) * (p - c)), где p - полупериметр треугольника, а a, b и c - длины его сторон.
Квадрат - это частный случай параллелограмма, у которого все стороны равны друг другу и все углы прямые (90°). Его периметр выражается через формулу P = 4 * a, где a - длина стороны, а площадь равна S = a^2.
Круг - это фигура, у которой все точки на поверхности находятся на одинаковом расстоянии от центра. Его длина окружности выражается через формулу C = 2 * π * r, где r - радиус окружности, а площадь равна S = π * r^2.
Знание основных характеристик геометрических фигур позволяет проводить различные вычисления, строить графики и понимать их свойства и взаимосвязи.