Поиск максимального значения функции является одной из классических задач математического анализа. Она находит свое применение во многих областях, начиная от оптимизации и машинного обучения, и заканчивая физикой и экономикой. Однако решение этой задачи может быть нетривиальным, особенно если функция имеет сложную форму и существует множество возможных максимумов.
Для поиска максимального значения функции требуется эффективный алгоритм, который быстро и точно определяет точку, в которой функция достигает максимума. Существует несколько различных подходов к решению этой задачи, каждый из которых имеет свои преимущества и недостатки.
Одним из наиболее распространенных алгоритмов поиска максимума функции является метод дихотомии. Он основан на принципе деления отрезка пополам и последующем выборе половины, в которой находится максимум. Этот метод позволяет быстро сойтись к решению, но требует, чтобы функция была выпуклой и наличия только одного максимума на заданном промежутке. В случае наличия нескольких максимумов или сложной формы функции, метод дихотомии может дать неточные или неверные результаты.
Другим эффективным алгоритмом поиска максимума функции является метод градиентного спуска. Он основан на поиске локального максимума на основе величины градиента функции в каждой точке. Этот метод может быть применен к произвольной функции, но требует начального приближения и может сойтись только к локальному максимуму, а не к глобальному. Тем не менее, метод градиентного спуска часто используется в задачах оптимизации и машинного обучения.
Эффективные алгоритмы поиска максимального значения функции по графику
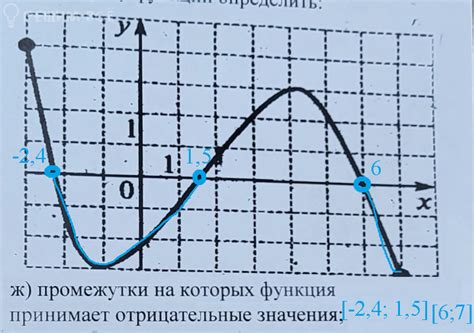
Существует несколько эффективных алгоритмов поиска максимального значения функции по графику. Один из таких алгоритмов - алгоритм дихотомии. Он предполагает разделение области поиска на две части и последующее повторение процедуры в нужной части. Алгоритм дихотомии обычно работает с функциями, которые монотонно возрастают или убывают на интервале.
Другим эффективным алгоритмом является алгоритм градиентного спуска. Он основан на итеративном поиске максимального значения функции в направлении, противоположном градиенту функции. Алгоритм градиентного спуска может быть использован для функций, которые не являются монотонными.
Также существуют алгоритмы, основанные на анализе кривизны функции. Например, алгоритмы Ньютона и квадратичной интерполяции могут использоваться для нахождения максимального значения функции.
Выбор конкретного алгоритма зависит от характеристик функции, таких как её гладкость, свойства градиента и выпуклость. Кроме того, эффективность алгоритма также может зависеть от доступности вычислительных ресурсов и времени, необходимого для выполнения поиска.
Важно отметить, что каждый алгоритм имеет свои достоинства и недостатки, и выбор алгоритма следует согласовывать с конкретными требованиями и ограничениями задачи.
Нахождение точек экстремума функции

Существует несколько эффективных алгоритмов для нахождения точек экстремума функции. Один из наиболее распространенных – метод дифференциальной эволюции. Он основан на имитации биологических процессов, а именно эволюции популяций.
Метод дифференциальной эволюции состоит из следующих шагов:
- Инициализация: создание начальной популяции значений переменных функции.
- Определение значения функции для каждого индивида популяции.
- Выбор лучшего индивида.
- Генерация новой популяции путем комбинирования значений переменных.
- Проверка условия останова (например, достижение предела числа итераций).
- Повторение шагов 2-5 до достижения условия останова.
В результате выполнения метода дифференциальной эволюции мы получаем точки экстремума функции, то есть значения переменных, при которых функция достигает своих максимума или минимума.
Еще одним эффективным алгоритмом для нахождения точек экстремума функции является метод градиентного спуска. Он основан на итеративном движении по градиенту функции с целью найти локальный экстремум.
Метод градиентного спуска состоит из следующих шагов:
- Инициализация: задание начального значения вектора переменных.
- Вычисление градиента функции в текущей точке.
- Изменение значений переменных в направлении, противоположном градиенту.
- Проверка условия останова (например, достижение предела числа итераций).
- Повторение шагов 2-4 до достижения условия останова.
Метод градиентного спуска позволяет найти локальные точки экстремума функции. Для поиска глобальных точек экстремума требуется использование модификаций данного метода, таких как методы случайного поиска или мультистартовые алгоритмы.
Все эти алгоритмы позволяют находить точки экстремума функции с высокой эффективностью и точностью. Их выбор зависит от конкретной задачи и требований к результатам.
Построение графика функции
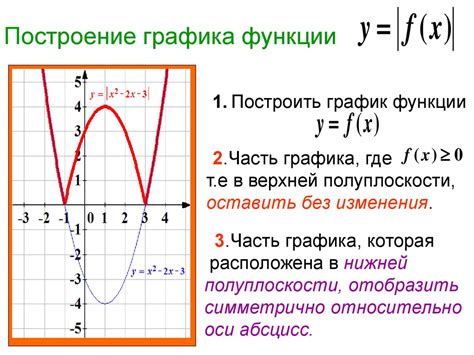
Для построения графика функции необходимо определить область определения и множество значений функции. Затем можно приступать к созданию координатной плоскости, где ось абсцисс соответствует аргументу функции, а ось ординат - ее значению.
Построение графика можно выполнить ручным способом или использовать программное обеспечение, которое расширит возможности и упростит процесс. Для ручного построения графика часто используются таблицы значений функции. Сначала значения аргумента выбираются в диапазоне области определения функции, затем по этим значениям вычисляются соответствующие значения функции. Полученные пары чисел отображаются на графике и соединяются ломаной линией или кривой.
Если же использовать программное обеспечение, то процесс построения графика может быть автоматизирован. Существует множество математических пакетов и графических редакторов, которые предоставляют широкие возможности для создания графиков функций. Эти программы позволяют регулировать масштаб графика, добавлять различные элементы (например, легенду, маркеры точек, оси координат) и применять различные стили линий и точек.
Важно отметить, что построение графика функции - это инструмент анализа функции, который позволяет получить точное представление о ее свойствах. Правильно построенный график может помочь в поиске максимального значения функции и определении оптимальных решений в различных задачах.
Определение максимального значения по графику
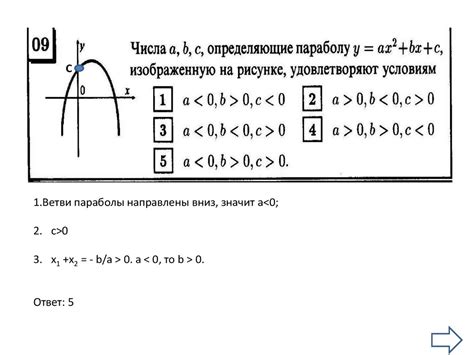
При работе с функциями и графиками часто возникает необходимость определить максимальное значение функции по графику. Это может быть полезным для многих задач, например, для оптимизации или анализа данных.
Для определения максимального значения по графику можно использовать различные алгоритмы. Один из самых эффективных алгоритмов поиска максимального значения по графику - это алгоритм двоичного поиска.
Алгоритм двоичного поиска позволяет быстро найти максимальное значение функции, имея только график функции и ограниченное число запросов. Он основывается на принципе "разделяй и властвуй", при котором задача разбивается на более простые подзадачи, решение которых затем комбинируется.
Для начала, необходимо определить интервал, в котором находится максимальное значение функции. Затем, используя алгоритм двоичного поиска, интервал разбивается на половины, и в каждой половине ищется максимальное значение функции. Это происходит до тех пор, пока не будет достигнута необходимая точность или пока не будет найдено максимальное значение функции.
Важно отметить, что для применения алгоритма двоичного поиска необходимо иметь возможность вычислять значение функции для произвольного аргумента. Также, алгоритм может быть эффективно применен только к монотонным функциям, т.е. функциям, которые либо возрастают, либо убывают на интервале.
Как можно видеть, определение максимального значения по графику является важной задачей при работе с функциями и графиками. Применение алгоритма двоичного поиска позволяет эффективно находить максимальное значение функции, что может быть полезным во многих областях, где требуется оптимизация или анализ данных.
Применение алгоритма дихотомии
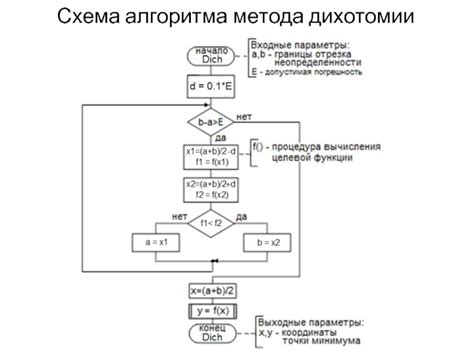
Применение алгоритма дихотомии позволяет найти максимальное значение функции на заданном интервале с минимальным количеством итераций. Алгоритм работает на основе свойства монотонности функции и заключается в следующих шагах:
- Задать начальные значения интервала и точность поиска.
- Вычислить середину интервала и значения функции в данной точке.
- Сравнить значение функции в середине интервала с максимальным найденным значением.
- Если значение функции больше максимального, обновить максимальное значение.
- Проверить, находится ли максимальное значение функции в левой или правой части интервала.
- Установить новые границы интервала в зависимости от результата предыдущего шага.
- Повторять шаги 2-6 до достижения заданной точности или пока не будет достигнута максимально возможная граница интервала.
Применение алгоритма дихотомии позволяет найти максимальное значение функции с использованием минимального количества вычислительных ресурсов. Он широко применяется в различных областях, таких как оптимизация, анализ данных, искусственный интеллект и другие.
Использование метода золотого сечения
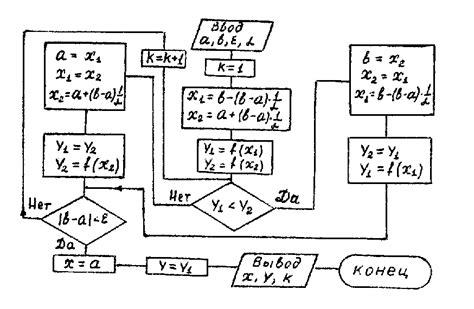
Данный метод может быть применен к функциям, которые обладают свойством унимодальности на заданном интервале. Функция называется унимодальной, если существует такая точка на интервале, что значения функции монотонно возрастают до этой точки и монотонно убывают после неё.
Алгоритм метода золотого сечения состоит из последовательного деления интервала по определенному соотношению золотого сечения. На каждой итерации алгоритма выбираются две точки на интервале, которые делят его отношением золотого сечения. Затем производится оценка значений функции в этих точках. Интервал с наименьшим значением функции сужается до тех пор, пока не будет достигнуто заданное условие остановки.
Использование метода золотого сечения позволяет достичь высокой точности при поиске максимального значения функции по её графику. Алгоритм имеет логарифмическую сложность и хорошо справляется с задачами оптимизации в реальных приложениях.
Преимущества метода золотого сечения:
- Высокая точность при поиске максимального значения функции
- Логарифмическая сложность алгоритма
- Применимость к унимодальным функциям
Использование метода золотого сечения является одним из эффективных подходов к оптимизации функций. Этот метод находит широкое применение в различных областях, включая науку, инженерию и экономику.