Машина Тьюринга - это универсальная вычислительная модель, разработанная английским математиком Аланом Тьюрингом в 1936 году. Она является одной из основных концепций теоретического компьютера и является базой для многих алгоритмов и принципов работы современных компьютеров.
Принцип работы машины Тьюринга основан на идеи использования бесконечной ленты, разделенной на ячейки, и головки, которая может перемещаться по этой ленте. В каждой ячейке ленты может храниться символ, а головка может читать и записывать символы, а также перемещаться влево или вправо. Машина Тьюринга может иметь внутреннее состояние, которое определяет последовательность действий, которые она выполняет над символами на ленте.
Операции, выполняемые машиной Тьюринга, определяются таблицей переходов, которая описывает, какая операция должна быть выполнена в зависимости от текущего состояния машины и символа на ленте. Программа на машине Тьюринга представляется в виде набора инструкций, где каждая инструкция состоит из текущего состояния, символа на ленте, операции (чтение, запись, перемещение головки) и нового состояния. Используя эти инструкции, машина Тьюринга может выполнять различные алгоритмические задачи, такие как сложение чисел, сортировка, проверка наличия определенного символа в последовательности и так далее.
Определение и основной принцип работы
Основной принцип работы машины Тьюринга заключается в обработке последовательности символов на бесконечной ленте. Машина состоит из следующих компонентов:
| Компонент | Описание |
|---|---|
| Лента | Бесконечная последовательность ячеек, каждая из которых содержит один символ из алфавита, состоящего из конечного числа символов. |
| Головка | Указатель на одну из ячеек ленты, позволяющий считывать и записывать символы. |
| Управляющее устройство | Логическая схема, которая определяет поведение машины в зависимости от текущего состояния и символа, считанного с текущей ячейки ленты. |
| Алфавит | Конечное множество символов, которые могут быть записаны на ленте. |
| Таблица переходов | Набор правил, определяющих, что делать машине в зависимости от текущего состояния и символа на ленте. |
Работа машины Тьюринга основана на последовательном применении таблицы переходов. В начале работы машина находится в некотором начальном состоянии и головка указывает на первую ячейку ленты. Затем машина последовательно считывает символ из текущей ячейки, применяет соответствующее правило из таблицы переходов, осуществляет перемещение головки и записывает новый символ в текущую ячейку. Процесс продолжается до тех пор, пока машина не достигнет конечного состояния или не выполнит определенное условие завершения.
История создания

Алан Тьюринг был одним из первых ученых, работавших над теорией вычислимости, и именно в рамках этих исследований он разработал принцип машины Тьюринга. В своей работе "On Computable Numbers, with an Application to the Entscheidungsproblem" он описал абстрактную машину Черча, которая позднее получила название "машина Тьюринга".
Машина Тьюринга была задумана как устройство с бесконечной лентой, на которую записываются символы. Устройство имеет головку, которая может читать и записывать символы на ленте и перемещаться вправо или влево. Машина Тьюринга также имеет внутреннее состояние, которое может изменяться в процессе работы.
Основная идея машины Тьюринга заключается в возможности моделирования любого алгоритма, используя простые правила чтения и записи символов на ленте, а также изменения состояний. Эта универсальность и абстрактность делает машину Тьюринга применимой во многих областях компьютерной науки, включая разработку алгоритмов и тестирование их эффективности.
В настоящее время машины Тьюринга являются основой для изучения теории вычислений и алгоритмов. Они также являются важным понятием в криптографии, теории сложности вычислений и теории формальных языков.
Алгоритмы машины Тьюринга
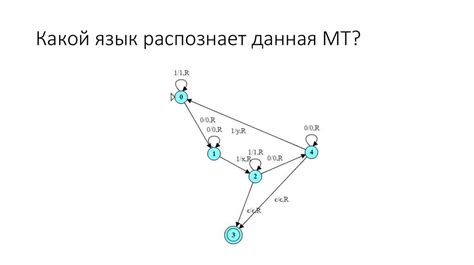
Алгоритмы машины Тьюринга описывают, как машина должна перемещаться по бесконечной ленте, обрабатывая символы, и принимать решения в зависимости от текущего состояния и символа, который она видит. Алгоритмы машины Тьюринга могут быть записаны в виде таблиц или графов, где каждое состояние машины и символ на ленте определяют следующее действие.
В алгоритмах машины Тьюринга используются различные операции, такие как перемещение влево или вправо по ленте, запись символа на ленту, стирание символа с ленты и изменение состояния машины. Алгоритмы машины Тьюринга могут быть простыми и состоять из нескольких шагов, или сложными и иметь множество разветвлений и условий.
Алгоритмы машины Тьюринга могут быть использованы для решения различных задач, включая вычисление математических функций, симуляцию других моделей вычислений и анализ алгоритмов. Они являются основой для теории вычислимости и применяются во множестве областей, таких как информатика, теория формальных языков, искусственный интеллект и криптография.
Важно отметить, что машина Тьюринга является универсальной вычислительной моделью, то есть любой алгоритм можно реализовать на машине Тьюринга. Это свойство делает машину Тьюринга мощным инструментом для исследования сложности алгоритмов и позволяет оценить возможности других моделей вычислений.
Применение и значимость

Машина Тьюринга имеет огромное применение в области вычислений и алгоритмов. Она служит основой для разработки и теоретического изучения различных алгоритмов, а также для исследования возможностей и ограничений вычислительных систем.
Одной из основных областей применения машины Тьюринга является теория вычислимости. Она позволяет формально описывать алгоритмы и доказывать их свойства, такие, как остановка или вычислимость. Благодаря этому, машина Тьюринга играет ключевую роль в разработке и анализе алгоритмов различных задач.
Важным применением машины Тьюринга является симуляция вычислений, осуществляемых на реальных компьютерах. С ее помощью можно анализировать производительность различных алгоритмов и оптимизировать их для достижения максимальной эффективности. Машина Тьюринга также используется для доказательства неразрешимости задач и понимания границ вычислительной сложности.
Значимость машины Тьюринга в теории вычислений трудно переоценить. Она является одной из основных моделей вычислений, на которых основана современная компьютерная наука. Без учета принципов работы и ограничений машины Тьюринга было бы значительно сложнее разрабатывать новые алгоритмы и понимать их свойства.
Концепция машины Тьюринга также имеет применение в других областях, таких, как искусственный интеллект, теория автоматов и логическое программирование. Она помогает в создании и анализе различных вычислительных моделей и формальных систем, а также в изучении сложности и возможностей искусственных интеллектуальных систем.