Уважаемые школьники-математики!

Вы наверняка знаете, что геометрия является одной из важных разделов математики. Она изучает различные геометрические фигуры и их свойства, а также взаимосвязь между ними. Сегодня у нас есть замечательная возможность попрактиковаться в построении геометрических фигур, а именно – пирамиды.

Пирамида – это трехмерная фигура, которая образуется путем соединения множества треугольников к одной точке – вершине. На самом деле, самым простым способом создать пирамиду не прибегая к сложным инструментам и материалам является использование обычной бумаги.

Классный мастер-класс по математике для школьников

Один из самых популярных мастер-классов - это создание пирамиды из бумаги. Учащиеся будут изучать геометрические фигуры, узнают, как строить пирамиды и сможут применить свои знания в практике. Этот мастер-класс поможет школьникам не только улучшить свои математические навыки, но и развить у них терпение, творческое мышление и сотрудничество.

Мастер-класс проводится под руководством опытного преподавателя-математика, который поможет детям разобраться в сложных концепциях и ответит на все их вопросы. Занятия будут проходить в игровой форме с использованием разнообразных материалов, включая цветную бумагу, ножницы и клей. Таким образом, школьники смогут не только учиться, но и развлекаться.

Мастер-класс по математике для школьников предлагает не только обучение, но и много полезных навыков для будущего. Например, умение работать в команде, решать проблемы и находить новые подходы к решению задач. Это занятие также поможет развить у детей уверенность в себе и усидчивость, что является важными качествами для успеха в учебе и жизни в целом.

Все участники мастер-класса получат не только знания в области математики, но и ощущение удовлетворения от решения сложных задач. Классные мастер-классы по математике для школьников стали популярными среди детей и их родителей, так как они не только обучают, но и весело проводят время. Поэтому не упустите возможность принять участие и провести интересное занятие, которое будет полезным для развития вашего ребенка!

Пирамида из бумаги: увлекательный способ изучения геометрии

Изготовление пирамиды из бумаги позволяет детям изучить основные понятия геометрии, такие как треугольник, пирамидальная вершина и боковая грань. Они смогут применить свои знания о геометрических пропорциях и отношениях для построения пирамиды правильной формы и размера.

Для создания пирамиды из бумаги потребуется использовать материалы, такие как цветная бумага, ножницы, клей и линейка. Школьники смогут самостоятельно изготовить шаблон пирамиды, вырезать его и собрать, следуя предложенной инструкции. Это поможет им развивать такие навыки, как точность, терпение и сосредоточенность.

Построение пирамиды из бумаги также может быть использовано в классе как интерактивное упражнение, где ученики работают в командах и совместно решают различные геометрические задачи. Это позволяет им применить свои знания на практике, обсуждать результаты и делиться своими идеями с другими участниками.

Таким образом, построение пирамиды из бумаги представляет собой увлекательный и практический способ изучения геометрии для школьников-математиков. Он помогает развивать навыки конструирования, пространственное мышление и понимание геометрических форм, а также способствует эффективному обмену идеями и опытом среди учеников.

Развитие логического мышления через конструирование

Конструирование через математические задачи помогает учащимся развивать свою способность к абстрактному мышлению. Они учатся анализировать условия задачи, прогнозировать возможные исходы, искать логические связи между элементами. Постепенно ребенок научится применять математические принципы и законы для решения сложных задач.

Конструирование также помогает развивать у детей навыки пространственного мышления. При создании различных структур и моделей, они учатся представлять объекты и формы в трехмерном пространстве. Это развивает их способность анализировать, визуализировать и манипулировать с объектами в пространстве.

Кроме того, конструирование способствует развитию креативности и воображения. Дети могут проявить свою индивидуальность и изобретательность, создавая уникальные конструкции и находя нестандартные решения. Это помогает им развивать свою интуицию и находчивость, которые также являются важными качествами для успешного решения математических задач.

Различные игры, головоломки и задания, основанные на конструировании, могут быть использованы учителями для разностороннего развития учащихся в школе. Они помогают детям лучше понять понятия математики и укрепить свои навыки в этой области.

Таким образом, конструирование является важным инструментом для развития логического мышления учащихся-математиков. Оно способствует развитию абстрактного мышления, пространственного воображения, креативности и интуиции. Конструирование позволяет учащимся лучше понять математические концепции и решать сложные задачи.

Математическая модель пирамиды: от оснований до вершины

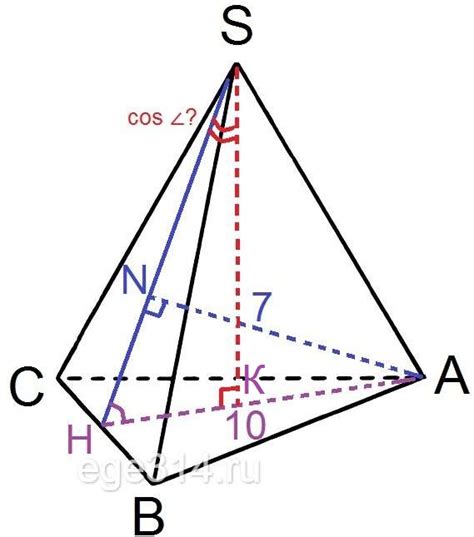
Математическая модель пирамиды представляет собой конструкцию, которая помогает нам лучше понять геометрические и арифметические свойства пирамиды. Она позволяет нам рассматривать отдельные части пирамиды и использовать их для решения задач и вычислений.

Основания пирамиды – это плоские фигуры, на которых она стоит. Они могут быть треугольниками, четырехугольниками или любыми другими многоугольниками. Размеры этих оснований определяют форму и размеры пирамиды.

Высота пирамиды – это перпендикуляр, опущенный из вершины на плоскость основания. Она является отрезком, соединяющим вершину пирамиды с центром основания. Высота пирамиды играет важную роль в вычислениях и определении объема пирамиды.

Математическая модель пирамиды позволяет проводить различные расчеты, такие как вычисление площади основания и боковых граней, определение объема и поверхности пирамиды, а также нахождение углов и длин сторон. Все эти вычисления имеют практическое применение, например, в строительстве, архитектуре и геодезии.

Использование математической модели пирамиды помогает учащимся лучше понять ее геометрические свойства, развивает навыки аналитического мышления и помогает решать задачи, связанные с этой фигурой. Математика – это не только формулы и числа, но и способ мышления, который позволяет нам исследовать мир вокруг нас, в том числе и пирамиды из бумаги.

Выкройка и сборка пирамиды: от теории к практике

Для создания пирамиды из бумаги нам потребуется знание основных геометрических принципов и некоторые математические вычисления. Отличная возможность показать, как математика имеет практическое применение в реальной жизни!

Первым шагом является создание выкройки пирамиды. Для этого возьмите кусок бумаги прямоугольной формы и отрежьте одну из сторон так, чтобы она стала квадратом. Этот квадрат будет основанием пирамиды.

Следующий шаг - вычисление высоты пирамиды. Зная длину стороны основания и высоту, мы можем применить формулу площади треугольника: S = 1/2 * a * h, где S - площадь треугольника, a - длина стороны основания, h - высота треугольника. Разделив площадь на длину стороны основания, мы получим высоту пирамиды. Используя математические навыки, мы можем точно рассчитать необходимую высоту.

Теперь переходим к сборке пирамиды. Возьмите выкройку и согните ее по диагоналям, чтобы получить четыре треугольника, сходящихся в одной точке. Затем согните боковые стороны треугольников, чтобы образовать боковые грани пирамиды.

Остается только соединить боковые грани пирамиды. Для этого используйте клей или скотч. Приклейте одну сторону пирамиды к другой, образуя четырехугольники. Для более прочной фиксации можно приклеить и дно пирамиды к боковым граням.

Таким образом, применяя математические знания и навыки, школьники-математики могут с легкостью создать пирамиду из бумаги. Это не только интересный мастер-класс, но и отличный способ показать важность математики в повседневной жизни.

Интерактивные задания и игры: учимся решать математические задачи весело!

Математика может быть увлекательной и интересной, особенно когда мы применяем ее на практике. В данном разделе рассмотрим несколько интерактивных заданий и игр, которые помогут школьникам-математикам закрепить материал и учиться решать задачи весело и с удовольствием.

Одной из популярных игр является "Математический манки". В этой игре нужно помочь обезьянке собрать все бананы, решая математические примеры. Чем быстрее и точнее ребенок отвечает на вопросы, тем больше бананов он собирает. Это отличный способ тренировать счет, сравнение чисел и арифметические операции.

Еще одной интересной задачей является "Загадки и головоломки". Ребенку предлагается решить разные математические загадки, которые требуют логического мышления и умения применять полученные знания. Каждый ответ помогает найти следующий кусочек головоломки, и в конце получается красивый рисунок.

Кроме того, существуют разнообразные онлайн-ресурсы и приложения, которые предлагают детям игровой подход к изучению математики. Например, "Mathletics" - это платформа с различными играми и тестами на разные возрастные группы. Здесь ребенок может соревноваться с другими учениками, отвечая на вопросы и получая за это очки.

Не забывайте также о классических играх, которые можно адаптировать для решения математических задач. Например, "Судоку" - головоломка, которая требует решения математических задач на логическом уровне. И с каждым разом, когда ученику удается решить головоломку, его навыки в математике улучшаются.

В завершение статьи хочется отметить, что интерактивные задания и игры помогают детям осознать важность математики и понять, что она может быть не только полезной, но и веселой. Благодаря игровому подходу, дети заинтересовываются математикой, развивают навыки решения задач, а также тренируют свою логику и смекалку.