Математика часто ассоциируется с неприятными воспоминаниями из школьной скамьи: бесконечные формулы, сложные решения, множество ошибок и разочарований. Однако, математика может быть не только увлекательной, но и простой! Существуют способы и методы, которые сделают решение сложных математических задач быстрым и легким.
Один из величайших математиков всех времен, Карл Фридрих Гаусс, считал, что математика – это "королева наук". Он понимал, что для успешного решения задач необходимо владеть не только знаниями, но и уметь применять различные методы и стратегии. В результате работы Гаусса были созданы такие инструменты, как метод Гаусса для решения систем линейных уравнений и метод наименьших квадратов для аппроксимации функций.
Сегодня существуют различные методы, которые помогают не только упростить, но и ускорить процесс решения сложных задач. Одним из таких методов является алгоритмический подход. Алгоритм – это четкая последовательность действий, с помощью которых можно решить конкретную задачу. Используя алгоритмический подход, можно разбить сложную задачу на более простые подзадачи и построить логическую цепочку действий.
Также в решении математических задач помогает аналогия. Часто задачи представляют собой предельно абстрактные конструкции, которые трудно понять. Аналогия помогает перенести задачу в конкретный контекст и, таким образом, найти решение. Например, при решении задачи о двух поездах, движущихся навстречу друг другу со скоростями 50 км/ч и 60 км/ч, можно представить эти поезда как два человека, бегущих навстречу друг другу со скоростями 5 км/ч и 6 км/ч.
Изучение математического хока

| Шаг | Описание |
|---|---|
| Шаг 1 | Определить задачу |
| Шаг 2 | Разбить задачу на более простые части |
| Шаг 3 | Использовать известные формулы и правила |
| Шаг 4 | Применить математические приемы и трюки |
| Шаг 5 | Проверить и объяснить результат |
Изучение математического хока требует времени и практики, но благодаря этой технике можно достичь впечатляющих результатов. Разбивая сложную задачу на более простые шаги и применяя математические приемы, можно сократить время на решение задачи и увеличить точность ответа. Упражнения по математическому хоку можно регулярно практиковать, чтобы повысить свои навыки и эффективность.
Краткий обзор этой техники

Основная идея математического хока заключается в том, что существует несколько универсальных стратегий, которые можно применять для решения большинства задач. Эти стратегии включают в себя различные математические операции, такие как сложение, вычитание, умножение и деление, а также использование факторизации, алгебраических формул и графиков.
Одним из ключевых преимуществ математического хока является его простота и доступность - даже люди без специального образования в области математики могут успешно использовать эту методику. С помощью математического хока можно быстро решить сложные задачи, которые обычно требуют больших усилий и времени.
Важным аспектом математического хока является умение найти оптимальный путь решения задачи - использовать наиболее эффективные приемы и техники, чтобы не тратить лишнее время на излишние вычисления или исследования. Эта навык не только увеличивает скорость решения задач, но и позволяет сэкономить ценное время на экзаменах и тестах.
Основные преимущества математического хока

| 1 | Быстрота | Математический хок позволяет решать задачи в несколько раз быстрее, чем традиционные методы. Благодаря определенным приемам и стратегиям, вы можете избегать лишних шагов и сокращать количество времени, затраченного на задачу. |
| 2 | Простота | Математический хок предлагает простые и легко запоминающиеся правила, которые помогут вам эффективно решать задачи. Нет необходимости выполнять сложные вычисления или запоминать длинные формулы. Все, что вам нужно, это понять основные принципы и применять их на практике. |
| 3 | Универсальность | Математический хок может быть применен к различным областям математики, включая алгебру, геометрию, тригонометрию и другие. Независимо от того, какая задача перед вами – нахождение корней уравнения, решение системы уравнений или вычисление площади фигуры – математический хок поможет вам решить ее быстро и легко. |
| 4 | Улучшение навыков | Применение математического хока помогает улучшить вашу математическую интуицию, логическое мышление и способность к анализу. Вы сможете видеть скрытые закономерности и использовать их для решения других задач. Это поможет вам стать более уверенными в своих математических навыках и получить более высокие оценки на экзаменах. |
В итоге, математический хок не только позволяет вам быстро решать сложные задачи, но и развивает вас как математика и повышает вашу успеваемость в этой науке.
Как правильно применять математический хок

Вот несколько ключевых принципов, которые помогут вам в правильном использовании математического хока:
- Ознакомьтесь с основами математических хоков. Изучите основные трюки, формулы и уловки, которые помогут вам решать сложные задачи быстрее и проще. Например, научитесь использовать принцип обратного порядка операций, факторизацию, приближенные значения и другие методы.
- Практикуйтесь и тренируйтесь. Решение математических задач с использованием хоков требует навыка и опыта. Постепенно увеличивайте сложность задач и применяйте математические хоки на практике, чтобы овладеть ими.
- Используйте логику и креативность. Математический хок - это не только овладение определенными методиками, но и умение мыслить логически и творчески. Используйте свои знания и интуицию для поиска нестандартных решений и упрощения задач.
- Обращайте внимание на детали. В решении сложных задач даже маленькие детали могут сыграть огромную роль. Внимательно анализируйте условия задачи, ищите скрытые подсказки и попробуйте использовать их в своем решении.
- Не забывайте проверять свои решения. Важно не только находить быстрое и простое решение, но и проверять его на корректность. Делайте контрольные вычисления и проверяйте полученные результаты, чтобы быть уверенными в правильности своих ответов.
Соблюдение этих простых правил поможет вам более эффективно использовать математический хок и достигнуть высоких результатов в решении сложных задач. Практика и постоянное улучшение собственных навыков помогут вам стать настоящим мастером математического хока.
Простые математические методы

В мире математики существует множество сложных и глубоких теорем, которые требуют многих лет изучения и понимания. Однако, помимо них существуют и простые математические методы, которые позволяют решать разнообразные задачи быстро и легко.
Один из таких методов - метод "приближения". Этот метод позволяет находить приближенное значение неизвестного числа, основываясь на определенных правилах и формулах. Например, для приближенного вычисления корня квадратного можно воспользоваться методом Герона или методом половинного деления.
Еще одним простым математическим методом является метод подстановки. Он заключается в замене неизвестных в уравнении на известные значения, что позволяет свести сложные уравнения к простым и решить их с помощью элементарной алгебры.
Также существуют методы оценки и сравнения чисел. Например, метод оценки количества цифр в числе, основанный на его порядке или метод отбора наименьшего числа путем сравнения первых цифр чисел.
Простые математические методы могут быть очень полезными в различных ситуациях. Они позволяют решать задачи быстро и эффективно, не требуя большого объема знаний и времени. Однако, важно помнить, что они не всегда дают точные ответы, и иногда может потребоваться применение более сложных методов для получения точного результата.
Использование упрощенных формул

В математике существует множество сложных формул, которые могут быть трудными для понимания и применения. Однако, существуют также упрощенные формулы, которые позволяют решать сложные задачи быстро и легко.
Упрощенные формулы являются альтернативными методами решения задач, которые помогают сократить время и усилия, необходимые для получения ответа. Они могут быть основаны на определенных математических принципах, связанных с алгеброй, геометрией или другими областями математики.
Использование упрощенных формул может быть полезно во многих ситуациях. Например, если вам нужно решить задачу на экзамене или важном испытании, использование упрощенных формул позволит сэкономить время и избежать ошибок.
Однако, необходимо помнить, что использование упрощенных формул требует определенных навыков и знаний. Необходимо правильно понять и применить формулу, чтобы получить правильный ответ. Также следует помнить, что упрощенные формулы не всегда применимы ко всем задачам, и иногда может потребоваться использование более сложных и точных методов.
Ускорение расчетов с помощью приближений

Для использования приближений необходимо уметь анализировать задачу и выяснить, в каких случаях точность может быть незначительно понижена. Например, при работе с большими числами, можно проигнорировать десятичные разряды после определенного порядка, так как они могут не иметь существенного влияния на конечный результат. Такой подход позволяет сократить количество вычислений и ускорить работу с задачей.
Еще одним способом ускорения расчетов с использованием приближений являются замены сложных математических операций более простыми аналогами. Например, сложение и умножение чисел с похожими порядками величин может быть заменено на более простые операции, такие как сдвиги и битовые операции. Это позволяет сократить количество вычислений и значительно ускорить работу с задачей.
Однако, при использовании приближений необходимо учитывать потери точности. Использование приближений может привести к небольшим погрешностям в вычислениях. Поэтому перед использованием приближений необходимо оценить их влияние на конечный результат и принять взвешенное решение о том, насколько допустимы погрешности в данной задаче.
Решение сложных задач

Первое, что нужно сделать при решении сложной задачи, это внимательно прочитать условие. Важно правильно понять, что от вас требуется и какую информацию вы получили. Затем, можно разбить задачу на более простые части и рассмотреть каждую из них отдельно.
Если вам сложно представить себе задачу в голове, попробуйте нарисовать схему или сделать небольшой рисунок. Это может помочь визуализировать информацию и прояснить некоторые детали. Также, полезно начать с простых примеров или использовать числа вместо переменных, чтобы лучше понять суть задачи.
Не стесняйтесь использовать различные математические приемы и методы, которые вы изучили ранее. Они могут оказаться очень полезными при решении сложных задач. Попробуйте разложить задачу на более простые компоненты, использовать алгебру, геометрию или другие математические инструменты в своих рассуждениях.
Если у вас возникают затруднения, не бойтесь обратиться за помощью. Можете попросить своих друзей или учителя с удовольствием помочь вам разобраться с задачей. Также, существует множество онлайн ресурсов и форумов, где вы можете задать вопросы и получить ответы от опытных математиков.
И последнее, но не менее важное - практика. Регулярная тренировка поможет вам улучшить свои навыки и стать более уверенным в решении сложных математических задач. Не бойтесь брать новые задачи, даже если они кажутся сложными, - это отличная возможность применить свои знания и развить свои навыки.
Применение разложения на множители
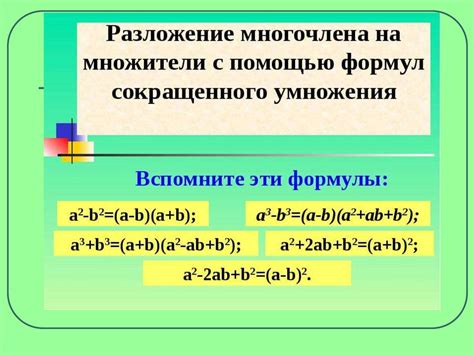
Применение разложения на множители особенно полезно для решения задач на поиск наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) двух чисел. Для этого необходимо разложить оба числа на множители и найти их общие простые множители.
Разложение на множители также помогает упростить выражения и решить уравнения. Например, при факторизации квадратного трехчлена, разложение на множители позволяет преобразовать его к виду произведения двух множителей и найти корни уравнения.
Важно знать основные правила разложения на множители, такие как разложение числа на простые множители, разложение полного квадрата, разность кубов и др. Это поможет быстро и легко решать сложные задачи и упрощать алгебраические выражения.
Применение разложения на множители – ключевой навык, который позволяет решать математические задачи эффективно и умно. Знание основных правил разложения и умение применять их в практике помогут вам стать настоящим математическим хоком.
Использование метода отражений

Основной принцип метода отражений заключается в следующем:
- Выбирается точка, относительно которой будет происходить отражение.
- Фигура отражается относительно выбранной точки.
- Полученное отражение анализируется для нахождения решения задачи.
Метод отражений широко используется в различных областях математики, физики и инженерии. Например, в геометрии он позволяет решать задачи на построение отражения фигур. В физике метод отражений применяется для изучения законов оптики и звука. В инженерии этот метод используется при проектировании антенн и зеркал, а также при моделировании процессов отражения электромагнитных волн.
Использование метода отражений требует навыков работы с геометрическими объектами и анализа полученных результатов. Однако, благодаря своей эффективности, этот метод является незаменимым инструментом для решения сложных задач в различных областях науки и техники.