Синус угла треугольника – это абсолютное значение отношения противолежащей стороны к гипотенузе. Поиск синуса угла треугольника может быть полезен при решении различных математических и геометрических задач.
Для нахождения синуса угла треугольника необходимо знать длины сторон: противолежащей углу и гипотенузы. Зная эти значения, можно применить формулу и получить результат.
В формуле синуса угла треугольника используются следующие обозначения: sin(A) – синус угла, a – противолежащая сторона, h – гипотенуза. Формула имеет вид: sin(A) = a / h. Например, если противолежащая сторона треугольника равна 4, а гипотенуза равна 8, то синус угла равен sin(A) = 4 / 8 = 0.5.
Знание формулы для нахождения синуса угла треугольника может быть полезным при решении задач на геометрию, тригонометрию, физику и другие науки. Это один из основных инструментов для работы с треугольниками и определения их свойств.
Что такое синус угла?

Синус угла можно определить как отношение противолежащего катета к гипотенузе в прямоугольном треугольнике. Он обозначается как sin(θ), где θ - угол треугольника.
Значение синуса угла может быть от -1 до 1 включительно. Если угол равен 90 градусам, то синус угла будет равен 1. Если угол равен 0 градусам, то синус угла будет равен 0.
Синус угла имеет ряд важных свойств, которые позволяют использовать его для решения различных задач. Например, синус угла может быть использован для нахождения длины стороны треугольника при известном угле и длине другой стороны.
Важно отметить, что значения синуса угла могут быть найдены с помощью таблицы синусов или с использованием специальных калькуляторов и программ.
Зная значения синуса угла, можно решать задачи, связанные с геометрией, физикой, компьютерной графикой и другими областями науки и техники.
Формула синуса для нахождения синуса угла
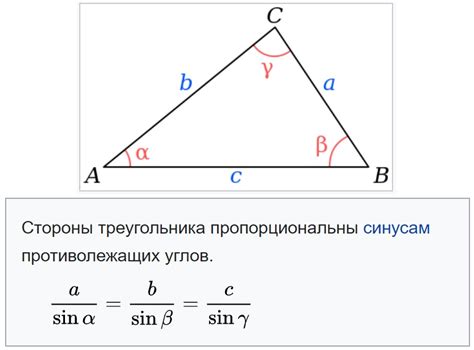
Для вычисления синуса угла используется формула синуса:
sin(α) = a / c
где:
- sin(α) – синус угла α;
- a – длина противоположной стороны угла α;
- c – длина гипотенузы треугольника.
Формула синуса позволяет выразить синус угла через соотношение между сторонами треугольника. Зная длины сторон, можно вычислить синус угла и использовать его для решения геометрических задач или построения графиков.
Где использовать синус угла?

Синус угла широко используется в различных областях науки, техники, физики и математики. В астрономии, например, синус угла используется для измерения длины дуги на небесной сфере, а в физике - для описания гармонических колебаний и волн. Также синус угла находит свое применение в инженерии, строительстве и геодезии, где используется для измерения высоты, углов наклона и расстояний.
Синус угла также находит применение в компьютерной графике, где используется для расчета и визуализации трехмерных моделей и анимаций. Он также важен в многих других областях, таких как радиотехника, электротехника, сигнальная обработка, статистика и финансовые модели.
Таким образом, синус угла играет важную роль в различных областях науки и техники, обеспечивая точные значения и решения для различных задач и проблем.
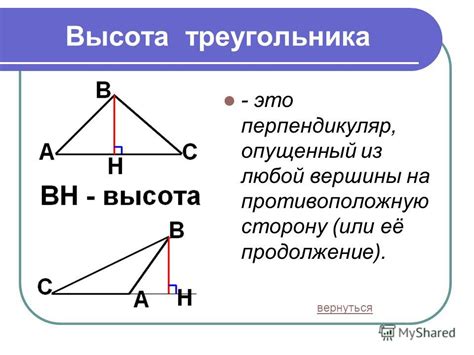
Треугольник и его углы
Углы треугольника измеряются в градусах и являются основой для решения множества задач, связанных с тригонометрией, геометрией и физикой. В треугольнике всегда существуют три угла, обозначаемых либо малыми латинскими буквами a, b, c, либо буквами, соответствующими вершинам треугольника.
Сумма всех углов треугольника всегда равна 180 градусам. В то же время, каждый угол треугольника не может быть больше 180 градусов.
Угол, расположенный напротив наибольшей стороны треугольника, называется большим углом. Противоположная этому углу сторона называется основанием. Меньшие углы треугольника называются меньшими углами.
Использование тригонометрических функций, таких как синус, косинус и тангенс, позволяет рассчитывать значения углов треугольника и решать разнообразные задачи, связанные с геометрией и физикой.
| Сторона | Угол |
|---|---|
| BC | a |
| AC | b |
| AB | c |
Определение треугольника
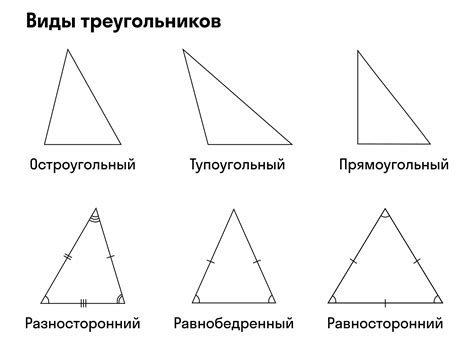
Треугольники могут быть классифицированы по различным критериям. Одним из основных критериев является их внутренний угол. Относительно внутренних углов, треугольники могут быть разделены на три типа:
- Остроугольный треугольник: все его углы острые, меньше 90 градусов.
- Прямоугольный треугольник: один из его углов равен 90 градусам.
- Тупоугольный треугольник: один из его углов больше 90 градусов.
Кроме того, треугольники могут быть классифицированы по длинам их сторон. В зависимости от этого, они могут быть равносторонними (все стороны равны), равнобедренными (две стороны равны) или разносторонними (все стороны различны).
Знание типа треугольника и его свойств позволяет нам определить, как вычислить его углы и стороны, включая синус угла. Синус угла - это отношение противолежащей стороны к гипотенузе в прямоугольном треугольнике, а также может быть вычислен в некоторых остроугольных треугольниках.
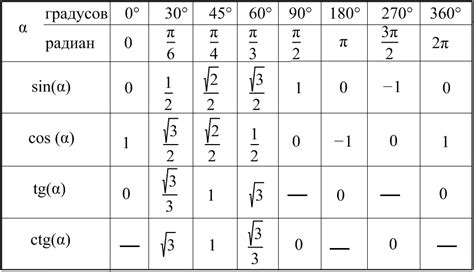
Таблица значений синуса
Угол (градусы)
0
30
45
60
90
Синус угла
0
0.5
0.7071
0.866
1
Таким образом, зная угол, можно найти его синус, сравнив его значение в таблице. Это поможет в решении задач, требующих вычисления синуса угла треугольника.
Примеры решения задач на нахождение синуса угла

- У нас есть прямоугольный треугольник со сторонами a = 3 и b = 4. Нам необходимо найти синус угла α между гипотенузой и катетом.
Решение: В данной задаче можно использовать теорему Пифагора для нахождения гипотенузы, которая равна с = √(a² + b²) = √(3² + 4²) = √(9 + 16) = √25 = 5.
Затем используем формулу sin α = a / c = 3 / 5 = 0.6.
- У нас есть произвольный треугольник со сторонами a = 5, b = 7 и углом γ = 30°. Нам необходимо найти синус угла γ между этим углом и стороной с длиной 5.
Решение: В данной задаче можно использовать применение закона синусов, поскольку мы знаем соотношение между углами и соответствующими сторонами. Закон синусов гласит: a / sin α = b / sin β = c / sin γ.
Зная значения α и a, мы можем переписать формулу: sin γ = (a * sin β) / b = (5 * sin 30°) / 7 = 2.5 / 7 = 0.36.
- У нас есть равнобедренный треугольник со сторонами a = 5 и b = 5. Нам необходимо найти синус угла α между основанием и боковой стороной.
Решение: Равнобедренный треугольник имеет особенность - медиана, биссектриса, высота и центральный угол, проведенные из вершины, ортогональны основанию треугольника. Значит, угол между основанием и боковой стороной равен половине центрального угла треугольника. Значит, sin α = sin (θ/2), где а = б и θ - центральный угол треугольника. Зная значения a и a, мы можем найти синус угла α: sin α = sin (θ/2) = sin (180°/2) = sin 90° = 1.