Цилиндр – это геометрическое тело, образованное вращением прямоугольника вокруг одной из его сторон. Осевым сечением цилиндра является плоскость, которая пересекает его ось в любой точке. Поиск диагонали осевого сечения цилиндра может быть полезной задачей в различных областях науки и техники.
Для нахождения диагонали осевого сечения цилиндра необходимо знать его радиус и высоту. Диагональ осевого сечения представляет собой отрезок, соединяющий две противоположные точки на пересечении сечения с боковой поверхностью цилиндра. Данная величина может быть искомой при решении задач по определению объема, площади или других характеристик цилиндра.
Для вычисления диагонали осевого сечения цилиндра используется теорема Пифагора, так как она позволяет найти гипотенузу прямоугольного треугольника, если известны его катеты. В данном случае, катетами выступают радиус и высота цилиндра. Путем подстановки значений в формулу и выполнения вычислений можно получить искомую диагональ осевого сечения цилиндра.
Что такое диагональ осевого сечения цилиндра?

Для определения диагонали осевого сечения необходимо провести прямую линию, которая начинается в одной точке плоскости поперечного сечения, проходит через центр цилиндра и заканчивается в противоположной точке на этой же плоскости. Длина диагонали осевого сечения может быть определена с использованием теоремы Пифагора или других геометрических методов.
Знание диагонали осевого сечения цилиндра позволяет решать различные задачи, связанные с геометрией цилиндров и их свойствами. Также это понятие используется в инженерии, архитектуре и других областях, где цилиндры широко применяются.
Зачем нужно находить диагональ осевого сечения цилиндра?

Существуют несколько причин, по которым необходимо знать значение диагонали осевого сечения цилиндра:
- Расчет объема и площади поверхности цилиндрического объекта. Для более точного определения этих параметров требуется знание длины диагонали осевого сечения.
- Планирование и проектирование строительных и архитектурных объектов. Размеры диагонали осевого сечения цилиндра позволяют определить взаимное расположение и пространственную ориентацию различных элементов.
- Механика и инженерия. Зная длину диагонали осевого сечения цилиндра, можно оценить его механическую прочность и выявить возможные проблемы с конструкцией.
- Разработка и проектирование транспортных и энергетических систем. В этих областях знание диагонали осевого сечения цилиндра позволяет оптимизировать работу и повысить эффективность различных систем.
Таким образом, нахождение диагонали осевого сечения цилиндра имеет практическую значимость для решения различных задач в науке, строительстве, проектировании и технике. Эта информация позволяет более точно определить размеры, характеристики и свойства цилиндрических объектов.
Примеры задач, в которых необходимо найти диагональ осевого сечения цилиндра

1. Задача на вычисление объема цилиндра. Если известны высота цилиндра и его радиус основания, то можно использовать формулу для вычисления объема цилиндра V = πr^2h. Но иногда нужно знать диагональ осевого сечения, чтобы решить данную задачу.
2. Задача на определение массы цилиндра. Если известны плотность материала, из которого сделан цилиндр, его объем и высота, то можно использовать формулу для вычисления массы M = pV, где p – плотность, V – объем. Опять же, диагональ осевого сечения может понадобиться для решения этой задачи.
3. Задача на определение момента инерции цилиндра. Момент инерции – это величина, характеризующая способность тела сохранять свою угловую скорость. Для цилиндра момент инерции может быть вычислен по формуле I = (1/2)mR^2, где m – масса цилиндра, R – радиус его осевого сечения. Диагональ осевого сечения понадобится для определения радиуса R.
Это лишь некоторые примеры задач, в которых необходимо найти диагональ осевого сечения цилиндра. Понимание геометрических свойств цилиндра и умение применять соответствующие формулы позволят успешно решать подобные задачи.
Учебный пример: нахождение диагонали осевого сечения цилиндра

Для нахождения диагонали осевого сечения цилиндра необходимо знать радиус сечения и высоту цилиндра. Рассмотрим пример:
- Известно, что радиус сечения цилиндра равен 5 см.
- Также известна высота цилиндра, которая составляет 10 см.
- Для нахождения диагонали осевого сечения цилиндра воспользуемся теоремой Пифагора.
Теорема Пифагора гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В нашем случае, гипотенуза - это диагональ осевого сечения цилиндра, а катеты - это радиус и высота цилиндра.
Применяя теорему Пифагора, получаем:
диагональ^2 = радиус^2 + высота^2
Подставляя известные значения, получаем:
диагональ^2 = 5^2 + 10^2
диагональ^2 = 25 + 100
диагональ^2 = 125
Чтобы найти диагональ, возьмем квадратный корень из значения 125:
диагональ = √125 ≈ 11.18 см
Итак, диагональ осевого сечения цилиндра равна приблизительно 11.18 см.
Таким образом, нахождение диагонали осевого сечения цилиндра может быть полезным при решении геометрических задач и в инженерии.
Советы по нахождению диагонали осевого сечения цилиндра
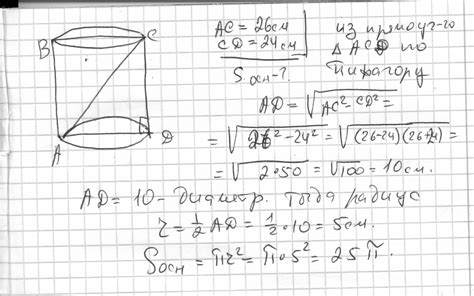
Нахождение диагонали осевого сечения цилиндра может быть полезным для решения различных задач и вычислений. Вот несколько советов, которые помогут вам найти эту величину:
- Изучение свойств цилиндра: перед тем, как начать искать диагональ осевого сечения, полезно вспомнить некоторые свойства цилиндра. Например, цилиндр состоит из двух плоских оснований и боковой поверхности, которая представляет собой криволинейную область между этими основаниями.
- Поиск формулы для вычисления диагонали: для нахождения диагонали осевого сечения цилиндра можно использовать геометрические формулы. Например, если вам известны радиус основания цилиндра (r) и высота (h), то диагональ осевого сечения можно найти с помощью теоремы Пифагора: диагональ^2 = (2 * r)^2 + h^2.
- Измерение размеров цилиндра: если у вас есть физический цилиндр, то можно измерить его размеры с помощью линейки или мерной ленты. Например, вы можете измерить радиус и высоту основания, а затем использовать полученные значения в формуле для вычисления диагонали.
- Использование математических программ или калькулятора: если у вас нет физического цилиндра или вы не хотите проводить ручные вычисления, вы можете использовать математические программы или калькуляторы. Введите известные значения (радиус и высоту) в программу, а она автоматически рассчитает диагональ осевого сечения цилиндра.
Следуя этим советам, вы сможете найти диагональ осевого сечения цилиндра и использовать эту информацию в различных задачах. И помните, что практика и изучение геометрии могут помочь вам лучше понять эти концепции и улучшить ваши навыки в решении математических задач.