Жорданов базис матрицы является важным инструментом в линейной алгебре. Он позволяет упростить анализ и работу с матрицами, особенно в случае наличия собственных значений с кратностью больше одного. Построение Жорданов базиса позволяет найти базис в пространстве, в котором данная матрица имеет каноническую форму.
Для построения Жорданов базиса необходимо выполнить несколько шагов. Сначала необходимо найти все собственные значения матрицы. Затем для каждого собственного значения найти его геометрическую кратность и найти базисное подпространство, соответствующее данному собственному значению.
Далее следует найти базис в каждом из базисных подпространств. В случае, когда собственное значение имеет кратность больше одного, базис в базисном подпространстве будет состоять из некоторых векторов, называемых жордановыми векторами. Жордановы векторы являются обобщенными собственными векторами и позволяют представить матрицу в канонической форме.
Что такое Жорданов базис матрицы
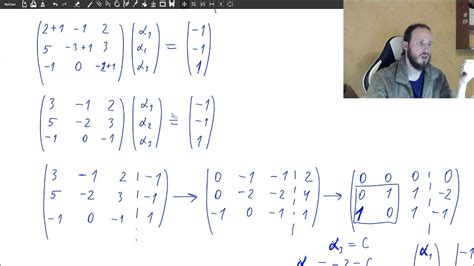
Матрица Жордана представляет собой блочно-диагональную матрицу, в которой на диагонали расположены блоки Жордана. Каждый блок Жордана имеет следующую структуру:
λ 1 И 1
0 λ 1
где λ 1 – собственное значение матрицы, которому соответствует этот блок.
Жорданов базис отличается от обычного базиса тем, что базисные вектора выбираются таким образом, чтобы каждый вектор был собственным для матрицы и принадлежал одному из блоков Жордана.
Построение Жорданова базиса позволяет упростить дальнейшие операции с матрицей, такие как вычисление ее преобразований и нахождение ее степеней. Кроме того, Жорданов базис может быть полезен при решении систем линейных уравнений и изучении свойств матрицы.
Запомните: Жорданов базис матрицы – это специальный вид базиса, который делает матрицу Жордана более удобной для анализа и вычислений.
Определение Жорданова базиса
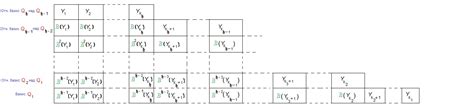
Жорданов базис используется для упрощения анализа матриц и решения различных задач, например, вычисления собственных значений и собственных векторов, а также для изучения структуры матрицы и ее свойств.
Жорданов базис состоит из векторов, которые являются образующими пространства, в котором действует матрица. Такие векторы являются собственными векторами матрицы и имеют особенности, связанные с ее структурой.
Основная особенность Жорданова базиса заключается в том, что каждый собственный вектор имеет связанный с ним блок Жордана, который представляет собой квадратную матрицу с собственным значением на главной диагонали и единицами на верхней поддиагонали.
Получить Жорданов базис можно с помощью преобразования матрицы к Жордановой нормальной форме с использованием алгоритма Жорданова разложения. Этот алгоритм заключается в построении базиса, состоящего из собственных векторов и векторов, которые являются образующими ядра матрицы после соответствующих преобразований.
Жорданов базис позволяет упростить вычисления с матрицами, так как он позволяет описать матрицу в виде блоков Жордана и использовать их свойства для анализа матрицы и ее операций.
Что такое базис в линейной алгебре

Базисный набор векторов задает координатную систему в пространстве, где каждый вектор представляется уникальным набором координат. Любой вектор в пространстве может быть выражен линейной комбинацией базисных векторов.
Размерность пространства определяется числом векторов в базисе. Если базис содержит n векторов, то говорят, что пространство имеет размерность n.
Базис может быть представлен в виде таблицы, где каждый столбец представляет собой координаты одного из базисных векторов. Такая таблица называется матрицей базиса. Матрица базиса является невырожденной и имеет полный ранг.
| Вектор 1 | Вектор 2 | ... | Вектор n |
|---|---|---|---|
| координаты 1 | координаты 2 | ... | координаты n |
Базис важен для изучения и понимания линейных операций, таких как умножение матриц, нахождение решений систем линейных уравнений и решения задач линейной оптимизации. Он также играет ключевую роль в теории Жордановой нормальной формы и построении Жорданового базиса матрицы.
Описание Жорданова базиса матрицы
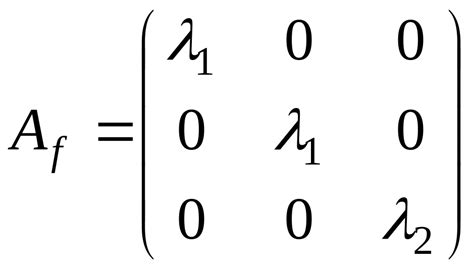
Жорданова клетка - это квадратная матрица, у которой все элементы на главной диагонали равны одному и тому же числу, все элементы на первой наддиагонали равны единице и все остальные элементы равны нулю. Размерность Жордановой клетки равна количеству единиц на первой наддиагонали.
Жорданов базис можно построить для любой матрицы над полем комплексных чисел, причем матрица и ее Жорданов базис будут связаны друг с другом некоторым преобразованием подобия. Для построения Жорданова базиса применяются методы алгебраической и комплексной арифметики, которые позволяют находить корни характеристического полинома и находить собственные векторы для различных собственных значений.
Жорданов базис является важным инструментом в теории линейных операторов и используется во многих областях математики, физики и инженерии. Он позволяет эффективно анализировать и управлять линейными системами, решать задачи разложения, диагонализации и суммирования матриц, а также исследовать динамические системы с помощью матричных представлений.
Вычисление Жорданова базиса
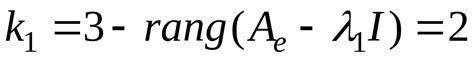
Для вычисления Жорданова базиса сначала нужно найти собственные значения матрицы. Это можно сделать с помощью характеристического полинома, который определяется как det(A - λI), где A - исходная матрица, λ - собственное значение, а I - единичная матрица того же порядка.
Затем для каждого собственного значения нужно найти жордановы клетки, которые соответствуют этому значению. Жорданова клетка - это квадратная матрица, у которой на главной диагонали стоят все равные собственному значению элементы, а над главной диагональю - единицы.
Для построения Жорданова базиса достаточно расставить жордановы клетки в правильном порядке. Количество и размерности этих клеток определяются алгебраической и геометрической кратностями собственного значения. Алгебраическая кратность - это количество всех корней характеристического полинома, а геометрическая кратность - это размерность собственного пространства.
Когда жорданов базис уже построен, его можно записать в виде матрицы, где блоки жордановых клеток стоят на главной диагонали, а остальные элементы заполняются нулями. Таким образом, Жорданов базис матрицы позволяет представить данную матрицу в более простом и структурированном виде.
Алгоритм построения Жорданова базиса
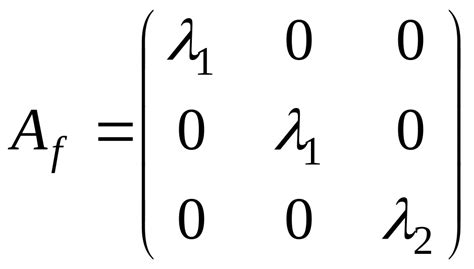
Для построения Жорданова базиса необходимо выполнить следующие шаги:
1. Найдите собственные значения матрицы и их алгебраические кратности. Алгебраическая кратность – это количество корней характеристического уравнения.
2. Для каждого собственного значения найдите собственный вектор и считайте его первым столбцом жорданова базиса. Если собственное значение имеет алгебраическую кратность больше 1, то строим остальные столбцы жорданова базиса, используя жордановы клетки.
3. Для построения жордановых клеток необходимо найти минимальное подпространство, порожденное собственным вектором и его образами при возведении в степень матрицы-оператора.
4. Заполните жорданову клетку значениями в соответствии с его размерностью.
5. Повторите шаги 2-4 для каждого собственного значения.
В результате выполнения алгоритма, матрица будет представлена в жордановой нормальной форме, а жорданов базис будет состоять из собственных векторов и их образов, полученных при возведении матрицы-оператора в степень.
Примеры вычисления Жорданова базиса матрицы

Для вычисления Жорданова базиса матрицы сначала нужно найти характеристический многочлен матрицы, а затем найти его корни. После этого можно построить жорданову форму матрицы и выбрать подходящую линейно независимую систему векторов в качестве базиса.
Приведем пример вычисления Жорданова базиса матрицы:
- Дана матрица A:
[2 1] [0 2]
- Для нахождения характеристического многочлена матрицы вычислим определитель матрицы (A - λI), где λ - переменная:
- Вычитаем переменную из диагональных элементов матрицы:
[2-λ 1 ] [0 2-λ]
Det(A - λI) = (2-λ)(2-λ) = (2-λ)^2 = λ^2 - 4λ + 4
- Решим уравнение λ^2 - 4λ + 4 = 0:
(λ-2)^2 = 0 λ = 2
- Размерность жорданового блока равна кратности корня:
[2 1] [0 2]
[2 1] [0 2]
- В данном случае можно выбрать векторы:
{ [1 0] , [1 1] }
Таким образом, Жорданов базис матрицы A состоит из векторов [1 0] и [1 1].
Применение Жорданова базиса
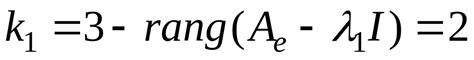
Одно из главных применений Жорданова базиса - это вычисление экспоненциальной функции от матрицы. Когда матрица не является диагональной, рассчет экспоненты может быть сложным и требовать много времени. Жорданов базис позволяет упростить этот процесс, так как в жордановой форме экспонента матрицы имеет простой вид.
Еще одно применение Жорданова базиса - это решение систем линейных дифференциальных уравнений. Жорданов базис помогает найти общее решение системы, что упрощает процесс анализа и позволяет получить более полную информацию о поведении системы.
Также Жорданов базис применяется в теории групп и теории представлений, где он используется для анализа симметрических и юнитарных матриц. Жорданов базис помогает найти инвариантные подпространства и классифицировать различные типы поведения матриц.
Все эти применения Жорданова базиса делают его важным инструментом для анализа и решения различных задач в математике и физике. Разумное использование Жорданова базиса позволяет упростить сложные вычисления и получить более подробную информацию о системе или матрице.
В чем преимущество использования Жорданова базиса
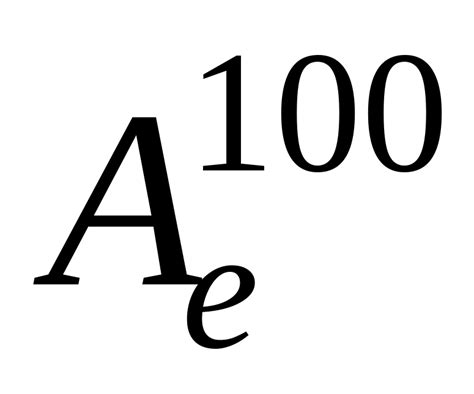
- Удобство в анализе и вычислениях: Жорданов базис позволяет значительно упростить анализ матрицы и выполнение вычислений с ней. Благодаря особому виду базисных векторов, можно быстро определить характеристики матрицы, такие как собственные значения и собственные векторы, а также выполнить операции с матрицей, такие как умножение и возведение в степень.
- Компактность представления: Жорданов базис позволяет компактно представить исходную матрицу в Жордановой нормальной форме. В этой форме, матрица представляется в виде суммы блоков Жордана, что значительно упрощает ее представление и позволяет сэкономить память.
- Устойчивость к погрешностям: Использование Жорданова базиса позволяет устранить или снизить влияние погрешностей, возникающих в процессе решения матричных уравнений. Благодаря особенностям Жорданова базиса, возможно существенно улучшить точность результатов и снизить вероятность ошибок.
Таким образом, использование Жорданова базиса предоставляет удобство в анализе и вычислениях, компактность представления матрицы и устойчивость к погрешностям, что делает его мощным инструментом в линейной алгебре и прикладных областях математики.