Параллелепипед - это геометрическое тело, у которого все грани являются прямоугольниками, а все ребра параллельны попарно. Одной из важных задач, связанных с изучением параллелепипедов, является поиск сечения через 3 точки. Этот метод позволяет определить плоскость, проходящую через три заданные точки на поверхности параллелепипеда.
Используя метод поиска сечения, можно решить множество задач, связанных с геометрией параллелепипеда. Например, определить, пересекаются ли два параллелепипеда, заданные точками, или определить взаимное расположение двух прямых в параллелепипеде.
Для применения данного метода необходимо указать три точки, через которые проходит сечение. Затем можно приступить к обработке этих данных. Сначала проводится прямая, проходящая через первые две точки. Затем находится ее пересечение с прямой, проходящей через вторую и третью точки. Таким образом, получаем точку пересечения этих прямых, которая будет задавать плоскость сечения.
Метод нахождения сечения параллелепипеда:
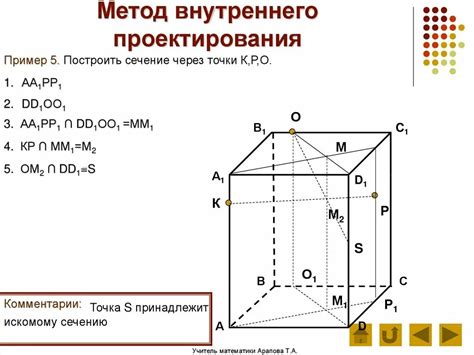
1. Находим плоскость, содержащую три заданные точки:
- Создаем векторы из первой точки ко второй и третьей точки. Найдем их векторное произведение, чтобы получить нормальный вектор плоскости.
- Проходим через одну из заданных точек и нормальный вектор, чтобы получить уравнение плоскости в виде Ax + By + Cz + D = 0.
2. Находим точки пересечения плоскости с гранями параллелепипеда:
- Находим пересечение плоскости с каждой гранью параллелепипеда, состоящей из двух параллельных сторон.
- Полученные точки пересечения являются вершинами сечения.
3. Соединяем вершины сечения:
- Соединяем вершины каждой пары, образующей соседние стороны сечения.
- Полученные отрезки являются ребрами сечения.
4. Отображаем результат:
Инструкция по поиску сечения через 3 точки

Чтобы найти сечение параллелепипеда через 3 точки, вам понадобятся следующие инструкции:
- Проверьте, что у вас есть все необходимые данные. Вам понадобятся координаты трех точек, через которые проходит секущая плоскость.
- Определите уравнение плоскости. Используя методы линейной алгебры, вычислите коэффициенты уравнения плоскости через данные точки.
- Разложите координаты вершин параллелепипеда, используя координаты его центра и длину его сторон. Получите список координат вершин.
- Проанализируйте, какие вершины параллелепипеда расположены по разные стороны от найденной плоскости. Вы можете использовать уравнение плоскости для определения относительного положения точек.
- Создайте новый множитель для хранения вершин, которые входят в сечение. Переберите все вершины параллелепипеда и добавьте те, которые расположены на секущей плоскости или в ее окрестности.
- Выведите список вершин, которые образуют сечение параллелепипеда.
Следуя этим инструкциям, вы сможете легко и точно найти сечение параллелепипеда через 3 заданные точки. Удачи в ваших изысканиях!
Простой способ определения сечения
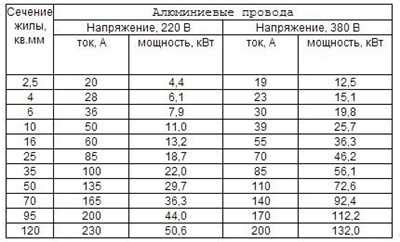
Существует простой способ определения сечения параллелепипеда через 3 точки. Для этого необходимо следовать следующим шагам:
- Задайте три точки в трехмерной системе координат, представляющие вершины параллелепипеда.
- Определите векторы, соединяющие эти точки: AB, AC и BC.
- Используя найденные векторы, вычислите их скалярное произведение:
| Vектор AB | Vектор AC | Vектор BC | |
|---|---|---|---|
| Координаты | (x2 - x1, y2 - y1, z2 - z1) | (x3 - x1, y3 - y1, z3 - z1) | (x3 - x2, y3 - y2, z3 - z2) |
Примечание: x1, y1, z1, x2, y2, z2, x3, y3, z3 - координаты соответствующих вершин.
- Если скалярное произведение векторов равно нулю, это означает, что 3 точки лежат на одной плоскости, а следовательно, они образуют сечение параллелепипеда.
- Если скалярное произведение векторов не равно нулю, это означает, что 3 точки не лежат на одной плоскости и не образуют сечение параллелепипеда.
Таким образом, применяя этот простой способ определения сечения, вы сможете легко выявить, являются ли заданные точки сечением параллелепипеда или нет.
Описание и примеры применения метода поиска сечения параллелепипеда:
Примеры применения данного метода могут быть следующими:
- Определение формы и размеров окна в здании. Установив три точки на разных уровнях окна и зная координаты этих точек, можно определить форму окна и его размеры для проектирования или ремонта.
- Анализ сечения трубы. Путем выставления трех точек на разных участках трубы и получения их координат, можно определить форму и размеры сечения трубы, что важно для монтажа и ремонта систем водоснабжения или отопления.
- Построение сечения детали. Посредством определения трех точек на различных участках детали и их координат, можно построить сечение данной детали и анализировать его форму для изготовления или ремонта.
Метод поиска сечения параллелепипеда через 3 точки является удобным способом определения формы и размеров сечения геометрического тела. Его применение может быть полезным в различных областях, где необходимо анализировать и конструировать сечения различных объектов.
Описание метода нахождения сечения параллелепипеда через 3 точки
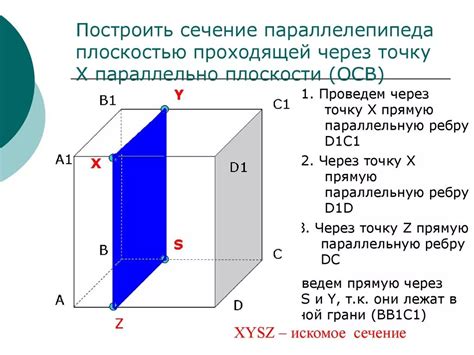
Для нахождения сечения параллелепипеда через 3 точки необходимо следовать определенному методу, который позволяет получить точные результаты.
1. Найдите координаты всех трех точек, через которые должно проходить сечение параллелепипеда. Обозначим их как A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3).
2. Вычислите векторы AB и AC, используя формулу: AB = B - A и AC = C - A. Эти векторы будут описывать направление сечения от точки A до точек B и C.
3. Найдите векторное произведение векторов AB и AC. Для этого используйте формулу: AB x AC = (y2 - y1)(z3 - z1) - (y3 - y1)(z2 - z1), (x3 - x1)(z2 - z1) - (x2 - x1)(z3 - z1), (x2 - x1)(y3 - y1) - (x3 - x1)(y2 - y1).
4. Проверьте, является ли полученный векторное произведение ненулевым вектором. Если координаты векторного произведения не равны нулю, то оно не является нулевым вектором и сечение через указанные точки существует. В противном случае сечение не существует.
5. Если сечение существует, найдите его параметрическое уравнение. Координаты точки A остаются неизменными, а направляющие векторы сечения будут равны AB и AC.
6. Визуализируйте сечение параллелепипеда с помощью графического редактора или специализированных программ. Это поможет увидеть конкретное положение сечения относительно параллелепипеда.
Используя описанный метод, вы сможете точно определить сечение параллелепипеда через 3 указанные точки. Этот метод удобен и применим в различных сферах, где требуется точное нахождение сечений.
Примеры использования метода нахождения сечения
Метод нахождения сечения параллелепипеда через 3 точки может быть полезен в различных областях, где требуется работа с трехмерными объектами. Вот несколько примеров использования этого метода:
| Пример | Описание |
|---|---|
| 1 | Архитектура и строительство |
| 2 | Геодезия и картография |
| 3 | Машиностроение и проектирование |
| 4 | Компьютерная графика и моделирование |
В архитектуре и строительстве этот метод может быть использован при проектировании зданий и сооружений. Например, можно использовать его для нахождения сечения стены или потолка, чтобы определить форму и размеры отверстия для установки окна или двери.
В геодезии и картографии метод нахождения сечения может быть полезен при создании топографических карт и моделей местности. Используя три точки на поверхности земли, можно определить высоту и форму рельефа, а также провести разрез местности, чтобы показать топографические особенности.
В машиностроении и проектировании этот метод может быть применен для создания трехмерных моделей и чертежей механических деталей и конструкций. Например, можно использовать его для нахождения поперечного сечения вала или трубы, чтобы определить их форму и размеры.
В компьютерной графике и моделировании метод нахождения сечения может быть использован для создания реалистичных трехмерных моделей и анимаций. Например, можно использовать его для нахождения сечения объекта в определенной плоскости, чтобы создать эффект разреза или просмотра внутренней структуры.
Преимущества использования метода поиска сечения параллелепипеда через 3 точки:
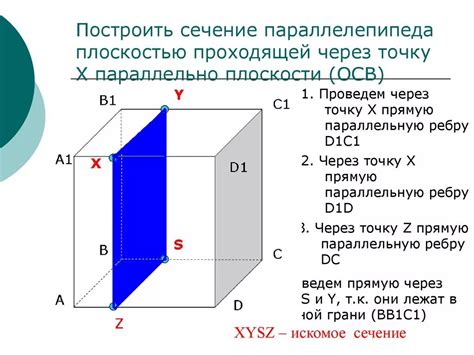
1. Точность: Метод обеспечивает высокую точность определения плоскости сечения параллелепипеда. Точки, через которые проходит плоскость, задаются с высокой точностью, что позволяет получить точное сечение.
2. Простота использования: Метод прост в использовании и не требует сложных математических вычислений. Для определения плоскости сечения достаточно задать координаты трех точек.
3. Универсальность: Метод применим для различных форм и размеров параллелепипеда. Он работает как для кубов, так и для прямоугольных параллелепипедов, а также для параллелепипедов с произвольными формами.
4. Геометрическая наглядность: Метод позволяет визуализировать сечение параллелепипеда через 3 точки. Это позволяет легко представить себе и понять, как будет выглядеть полученное сечение.
Поэтому использование метода поиска сечения параллелепипеда через 3 точки может быть полезным в различных областях, включая графику, архитектуру, строительство и другие.