Метод зон Френеля является одним из основных инструментов, которые используются в оптике для исследования волновых свойств света и других электромагнитных волн. Этот метод разработан французским физиком Огюстеном Френелем в начале 19 века и стал основой для понимания таких феноменов, как интерференция и дифракция света.
Метод зон Френеля основан на представлении световой волны как колебаний электрического и магнитного полей. Френель предположил, что на пути распространения света возникают концентрические зоны, внутри которых фаза световой волны постоянна. Таким образом, метод зон Френеля позволяет анализировать интерференцию и дифракцию световых волн, исходя из понятия зон с постоянной фазой.
Значение метода зон Френеля в оптике трудно переоценить. Он является неотъемлемой частью многих оптических систем и инструментов, таких как линзы, зеркала, призмы. Данный метод позволяет определить форму и размеры оптических элементов, а также их воздействие на характер световой волны.
Метод зон Френеля: суть и применение
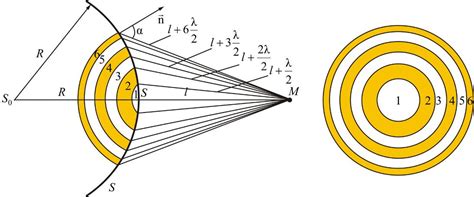
Основное предположение, лежащее в основе метода зон Френеля, заключается в том, что приближение параксиального света позволяет игнорировать изменение амплитуды светового поля и сосредоточиться только на фазовых изменениях. Таким образом, метод зон Френеля позволяет упростить анализ сложных оптических систем.
Применение метода зон Френеля находится во многих областях оптики. Он используется для описания дифракции света на краю препятствия, на отверстиях и сетках, а также в интерференции света. Метод зон Френеля позволяет рассчитывать форму и размеры образов, создаваемых оптическими системами, такими как линзы и зеркала.
Благодаря своей математической простоте и универсальности, метод зон Френеля является незаменимым инструментом в оптике. Он позволяет получить количественные оценки оптических явлений, прогнозировать их поведение и оптимизировать конструкцию оптических систем.
Принцип работы метода

Для того чтобы определить вид зон Френеля, необходимо знать амплитуду дифрагированной волны и амплитуду источника. Зная эти параметры, можно вычислить радиусы кривизны зон Френеля и положения их центров.
Дальнее поле дифракции выглядит как суперпозиция зон Френеля, каждая из которых представляет собой фокусирующую линзу. Изменение размеров зон и их положения в зависимости от расстояния до источника позволяет определить, какой вид имеет дифракционная картина.
| Зона Френеля | Радиус кривизны центральной точки | Положение центра |
| 1-я | r1 = √(d * λ) | (0, 0) |
| 2-я | r2 = √(2d * λ) | (0, λ/2) |
| 3-я | r3 = √(3d * λ) | (0, λ) |
| 4-я | r4 = √(4d * λ) | (0, 3λ/2) |
Таким образом, метод зон Френеля позволяет представить сложную дифракционную картину в виде простых элементов – зон, которые имеют определенные размеры и положение. Этот метод широко применяется в оптике для анализа дифракционных явлений и проектирования оптических систем.
Структура зон Френеля

Структура зон Френеля представляет собой периодическую последовательность зон разных радиусов и ширин, расположенных вокруг оптической оси. Каждая зона характеризуется фазовым сдвигом, который зависит от разности хода света внутри и вне зоны.
Первая зона или нулевая зона, называемая также центральной зоной, имеет наибольший радиус и нулевую разность хода, так как в этой зоне фазовый фронт проходит по прямому пути.
Следующие зоны имеют все больший радиус и соответствующую разность хода. Фазовый сдвиг в каждой зоне увеличивается на π по сравнению с предыдущей зоной.
Размер и количество зон Френеля определяются параметрами системы и длиной волны света. Чем больше длина волны по сравнению с размером препятствия или отверстием, тем больше будет количество зон. В пределе, когда размер препятствия или отверстия сравним с длиной волны, число зон Френеля бесконечно велико, что ведет к образованию непрерывного фазового фронта.
Структура зон Френеля позволяет описывать и объяснять различные дифракционные эффекты, такие как возникновение интерференции, образование дифракционных решеток и пространственных фильтров.
Математическое представление зон френеля

При изучении метода зон Френеля в оптике, необходимо ознакомиться с математическим представлением этих зон. Зоны Френеля представляют собой последовательность концентрических кругов, образующихся вблизи препятствия, через которое проходит световая волна.
Расстояние до точки наблюдения, где формируются эти зоны, называется радиусом Френеля. Математические выражения для радиуса Френеля и ширины зон можно вывести на основе суперпозиции волн. Радиус Френеля r можно определить по формуле:
r = sqrt(n*О*L)
где n - порядковый номер зоны, О - длина волны света, L - расстояние от препятствия до точки наблюдения.
Зная радиус Френеля, можно определить ширину zn каждой зоны Френеля:
zn = sqrt(n*О*L*λ)
где λ - длина волны света.
Математическое представление зон Френеля позволяет рассчитать их размеры и форму при различных условиях. Это является важной основой для применения метода зон Френеля в оптических системах и задачах.
Значение метода зон Френеля в оптике
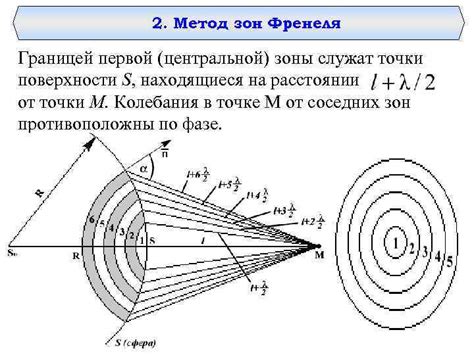
Суть метода заключается в разложении волнового фронта на сферические зоны Френеля, каждая из которых представляет собой кольцевую область с радиусом, соответствующим определенной разности хода световых лучей. Эти зоны образуются вследствие интерференции волн, их наложения друг на друга.
Метод зон Френеля позволяет рассчитать основные параметры рассеяния и преломления света, такие как фокусное расстояние, размер изображения и спектральное разрешение. Он широко используется в различных областях оптики, включая приборостроение, медицину, астрономию и многое другое.
Кроме того, метод зон Френеля также имеет практическое применение при расчете дифракционных явлений, таких как дифракция Фраунгофера и Френеля, интерференция света и аберрации в оптических системах. Он позволяет предсказать и объяснить ряд явлений, связанных с распространением света и оптическими системами.
Применение в фотонике

Метод зон Френеля нашел широкое применение в современной фотонике и оптике. Его применяют для анализа и проектирования оптических систем, таких как линзы, зеркала и другие устройства.
С помощью метода зон Френеля можно рассчитать фазовое распределение света вблизи фокуса или других фокусных плоскостей оптической системы. Это позволяет оптимизировать конструкцию системы и получить наилучшие оптические характеристики.
Кроме того, метод зон Френеля применяется в исследованиях фотонной кристаллографии и волноводов. Он позволяет исследовать распространение света в различных средах, рассчитывать дисперсию и поляризацию света.
Благодаря своей точности и универсальности, метод зон Френеля является одним из ключевых инструментов в фотонике и оптике. Он помогает улучшить проектирование и изготовление оптических систем, а также понять особенности взаимодействия света с веществом.
Роль в физической оптике

Основная роль метода зон Френеля состоит в определении распределения интенсивности света в местах, где в идеальных условиях оказывается наблюдатель. Метод позволяет вычислить разницу хода между различными элементами волнового фронта, а затем, используя принцип Гюйгенса-Френеля, найти суммарную амплитуду и интенсивность света.
Одним из наиболее известных примеров применения метода является изображение волнового поля линзы. Зоны Френеля позволяют оценить, каким будет распределение света в фокусной плоскости линзы. Также метод используется для анализа дифракции света на щели и периодических структурах.
Метод зон Френеля находит применение во многих областях оптики, таких как создание микро- и наноструктур, проектирование объективов и фокусных систем, интерферометрия, голография, фурье-оптика и другие. Он позволяет смоделировать распространение и взаимодействие света с неоднородными средами, что дает возможность создавать и анализировать сложные оптические системы.
| Преимущества метода зон Френеля: | Недостатки метода зон Френеля: |
|---|---|
| Простота и удобство расчетов | Ограничение применимости в сильно изогнутых поверхностях |
| Возможность получения качественного представления о распределении света | Не учитывает поляризацию света |
| Широкий спектр применения в различных областях оптики | Не учитывает влияние аберраций |
Таким образом, метод зон Френеля играет значительную роль в физической оптике, предоставляя возможность анализировать и моделировать световые поля в различных средах и структурах, а также помогает в проектировании и создании оптических систем.
Влияние на микро- и нанооптику
Влияние метода зон Френеля на микро- и нанооптику проявляется в нескольких аспектах:
Улучшение разрешающей способности Метод зон Френеля позволяет достичь более высокой разрешающей способности оптических систем на микро- и наноуровнях. Это особенно важно для изготовления микросхем, оптических волокон, сетчатых структур и других микро- и наноустройств, требующих высокой точности и детализации. | Управление распространением света Метод зон Френеля позволяет контролировать и изменять характер распространения света на микро- и наноуровнях. Это даёт возможность создания оптических элементов с заданными характеристиками, таких как линзы с переменным фокусом или формой, фазовые пластины и дифракционные оптические элементы. |
Изучение взаимодействия света и материи Метод зон Френеля позволяет более подробно изучить взаимодействие света с материей на микро- и наноуровнях. Это позволяет разрабатывать новые материалы, обладающие определенными оптическими свойствами, и применять их в различных областях – от оптокоммуникаций до солнечных батарей и электроники. | Разработка компактных оптических устройств Метод зон Френеля позволяет создавать компактные оптические устройства, такие как микроскопы, спектрометры и многие другие, с улучшенными характеристиками и меньшими габаритами. Это открывает новые возможности для применения оптики в микро- и нанотехнологиях. |
В целом, метод зон Френеля играет ключевую роль в развитии микро- и нанооптики, позволяя создавать более точные и эффективные оптические системы, а также открывая новые перспективы исследования и применения света на малых масштабах.