Котангенс треугольника является одним из основных тригонометрических понятий и дает возможность расчета отношения длины катета к длине прилежащего катета в прямоугольном треугольнике. На первый взгляд может показаться, что котангенс сложно определить, но на самом деле существуют несколько простых методов его вычисления.
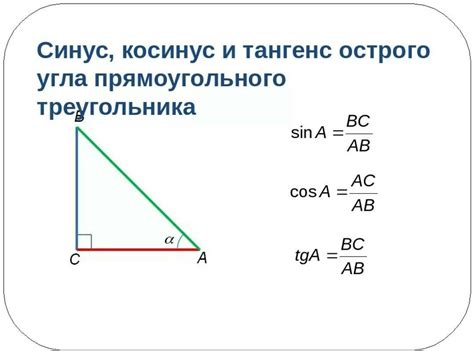
Один из самых распространенных методов определения котангенса основан на формуле: котангенс равен отношению катета, расположенного против ъгла, к катету, прилежащему к этому ъглу. Таким образом, формула для вычисления котангенса имеет следующий вид: cot A = b / a, где A - ъгол треугольника, b - противолежащий катет, а a - прилежащий катет.
Однако, помимо формулы расчета, существуют также и другие методы определения котангенса. Например, его можно вычислить, используя значения синуса и косинуса треугольника. В этом случае, котангенс равен отношению косинуса к синусу, поэтому формула принимает вид: cot A = cos A / sin A.
Изучение котангенса треугольника является важным для понимания тригонометрии и ее применения в различных областях науки и техники. Зная методы определения и формулу расчета котангенса, можно успешно применять его при решении задач в геометрии, физике, астрономии и других дисциплинах, где требуется работа с тригонометрическими функциями.
Что такое котангенс треугольника
Котангенс треугольника обозначается как cot или ctg и выражается с помощью формулы:
cot(A) = 1 / tan(A)
где A - угол треугольника, для которого необходимо вычислить котангенс.
Котангенс также может быть определен с помощью отношения косинуса угла к синусу:
cot(A) = cos(A) / sin(A)
Как и другие тригонометрические функции, котангенс может принимать значения в интервале от минус бесконечности до плюс бесконечности. Значение котангенса может быть использовано для определения углов треугольника, а также для нахождения длин сторон треугольника.
Формула и ее применение

Формула для вычисления котангенса (ctg) выглядит следующим образом:
| Угол | Котангенс |
|---|---|
| α | 1 / tan(α) |
| β | 1 / tan(β) |
| γ | 1 / tan(γ) |
Применение котангенса треугольника широко встречается в геометрии, физике и других науках. Он может использоваться для решения задач, связанных с вычислением углов, длин сторон и площадей треугольников. Кроме того, котангенс может быть полезен для определения высоты, радиуса описанной окружности и других параметров треугольника.