Нахождение минимума кривой - это одна из основных задач в математике и анализе данных. Многое зависит от того, какой метод или алгоритм выбрать для решения этой задачи. В данной статье мы рассмотрим основные подходы и примеры алгоритмов нахождения минимума кривой.
Одним из самых простых и популярных методов является метод градиентного спуска. Он основан на идее последовательного приближения к минимуму путем движения в направлении наиболее быстрого убывания функции. Для этого на каждой итерации вычисляется градиент функции и делается шаг в его противоположном направлении с некоторым шагом обучения. Этот процесс продолжается до тех пор, пока не будет достигнута заданная точность или не будет найден минимум функции.
Еще одним популярным подходом является метод наискорейшего спуска. В этом методе на каждой итерации выбирается наиболее "оптимальный" шаг таким образом, чтобы минимизировать функцию наиболее эффективным образом. Для этого используется метод золотого сечения или другие методы поиска минимума одномерной функции. Такой подход позволяет быстрее сойтись к минимуму кривой и повысить точность решения.
Примеры методов и алгоритмов нахождения минимума кривой можно найти во многих областях, таких как машинное обучение, оптимизация, анализ данных и других. Каждый метод имеет свои преимущества и недостатки, а выбор метода зависит от конкретной задачи и требований к результатам. Важно помнить, что нахождение минимума кривой - это сложная и многогранная задача, и выбор правильного метода может существенно повлиять на результаты и эффективность решения.
Жадный алгоритм
Основная идея жадного алгоритма заключается в том, чтобы на каждом шаге выбирать локально оптимальное решение, надеясь, что в итоге будет найдено глобальное оптимальное решение. Таким образом, алгоритм стремится к поиску минимума путем последовательного выбора наименьших значений или наиболее подходящих элементов.
Преимущества жадного алгоритма включают его простоту и эффективность. Он обладает низкой вычислительной сложностью и может быть применен для нахождения глобального минимума во многих задачах с ограниченными ресурсами. Но, к сожалению, жадный алгоритм не всегда гарантирует нахождение глобального минимума, и в некоторых случаях может давать только приближенное решение.
Примером использования жадного алгоритма для нахождения минимума кривой может быть задача о расстановке точек на прямой так, чтобы сумма расстояний от каждой точки до остальных была минимальной. Жадный алгоритм может быть применен для нахождения локально оптимального решения путем последовательного выбора точек с наименьшими расстояниями. Однако он не даст гарантии нахождения глобального минимума, и в этой задаче может потребоваться использовать другие методы и алгоритмы для достижения оптимального решения.
Метод половинного деления

Принцип работы метода состоит в следующем:
- Выбирается начальный интервал, на котором находится минимум кривой.
- Интервал делится пополам и находится среднее значение функции на полученных половинах.
- Анализируется полученное значение функции:
- Если значение функции равно 0, то найден корень и процесс завершается.
- Если значение функции на разных половинах имеет разный знак, то корень находится в одной из половин и процесс повторяется для этой половины.
- Если значение функции на разных половинах имеет одинаковый знак, то корень не находится в данном интервале и процесс повторяется для другой половины.
- Шаги 2-4 повторяются до тех пор, пока не будет достигнута заданная точность или найден минимум кривой.
Преимуществами метода половинного деления являются его простота реализации и гарантированная сходимость при условии непрерывности функции на заданном интервале. К недостаткам можно отнести относительно медленную скорость сходимости и возможное неудовлетворительное приближение при большом количестве итераций.
Приведем пример использования метода половинного деления для нахождения минимума функции на интервале [a, b]:
- Задаем начальный интервал [a, b] и точность epsilon.
- Пока b - a > epsilon, выполняем следующие шаги:
- Вычисляем среднюю точку c = (a + b) / 2.
- Вычисляем значения функции f(c), f(a) и f(b).
- Если значение функции f(c) равно 0, то c является минимумом и процедура завершается.
- Если f(c) * f(a) < 0, то корень находится на половине интервала [a, c], и b принимает значение c.
- Если f(c) * f(b) < 0, то корень находится на половине интервала [c, b], и а принимает значение c.
Метод половинного деления является одним из базовых методов оптимизации и широко используется в различных областях, где требуется нахождение минимума функции.
Метод градиентного спуска
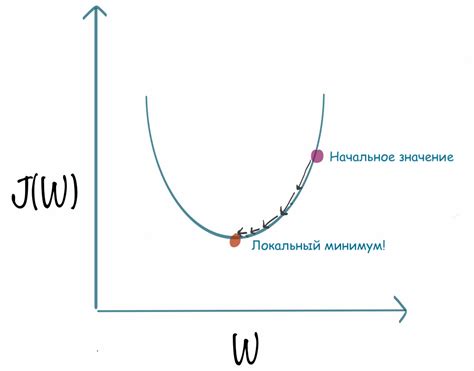
Основная идея метода заключается в том, что на каждой итерации выполняется шаг в направлении антиградиента функции, который определяется как отрицательная величина градиента. Шаги повторяются до тех пор, пока не будет достигнут минимум функции или пока не будет достигнут предел числа итераций.
Процесс метода градиентного спуска можно представить в виде следующего шагового алгоритма:
- Выбор начального приближения точки минимума.
- Вычисление градиента функции в этой точке.
- Движение вдоль антиградиента с шагом, определенным эвристически или с использованием оптимальных шаговых стратегий.
- Повторение шагов 2 и 3 до достижения условия сходимости или предела итераций.
Метод градиентного спуска имеет несколько вариантов, таких как стохастический градиентный спуск и мини-пакетный градиентный спуск, которые обеспечивают эффективность и применимость метода на практике, особенно при работе с большими объемами данных.
Применение метода градиентного спуска широко распространено в различных областях, включая машинное обучение, оптимизацию и нейронные сети. Он является мощным инструментом для нахождения минимума кривой и повышения производительности алгоритмов.
Метод Ньютона

Основная идея метода Ньютона заключается в использовании аппроксимации кривой вблизи точки минимума с помощью касательной. Для этого метод использует производные функции, чтобы найти точку пересечения касательной с осью абсцисс.
Алгоритм метода Ньютона можно представить в виде следующих шагов:
- Выбираем начальное приближение для минимума кривой.
- Вычисляем значение функции и ее производную в этой точке.
- Находим точку пересечения касательной с осью абсцисс.
- Повторяем шаги 2 и 3, пока не достигнем заданной точности или не выполним ограничение на количество итераций.
Преимущества метода Ньютона включают его высокую скорость сходимости и способность к нахождению минимума кривой с высокой точностью. Однако у метода Ньютона есть и недостатки, такие как требование задания начального приближения и возможность расходимости в случае некоторых функций.
Примером применения метода Ньютона может быть нахождение минимума функции f(x) = x2 - 4x + 4. В этом случае алгоритм метода Ньютона будет итеративно приближать минимум кривой к точке x = 2.
| Итерация | x | f(x) | f'(x) | Корень |
|---|---|---|---|---|
| 1 | 2 | 0 | -4 | 3 |
| 2 | 3 | -1 | -2 | 2.5 |
| 3 | 2.5 | -0.25 | -3 | 2.45 |
| 4 | 2.45 | -0.0025 | -3.1 | 2.4495 |
В данном примере метод Ньютона приближает минимум кривой к точке x = 2.4495 с каждой итерацией.
Метод сопряженных градиентов
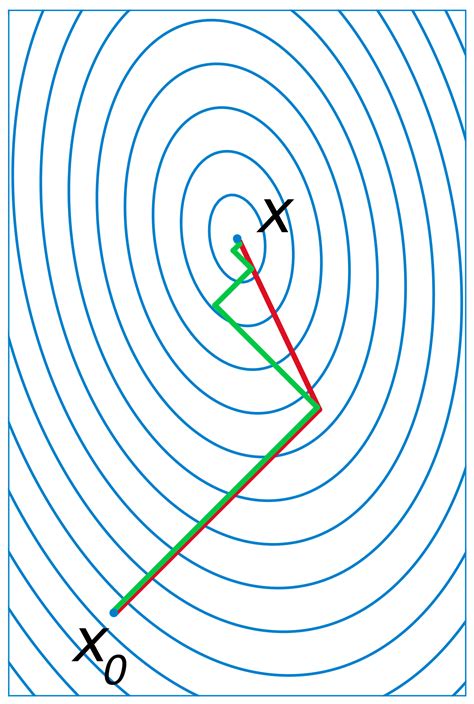
Суть метода заключается в последовательном движении по сопряженным направлениям градиента, в результате чего достигается быстрое сходство к минимуму кривой. Каждый новый шаг оптимизации выбирается таким образом, чтобы он перпендикулярен предыдущим направлениям и обеспечивает максимальное уменьшение функционала.
В методе сопряженных градиентов используется итерационный процесс, в котором вычисляются веса, определяющие обновление значения функционала и преобразование текущего состояния.
- На первом шаге веса равны градиенту функционала в точке минимума.
- На следующем шаге веса выбираются таким образом, чтобы они оказались сопряженными к предыдущему шагу.
- Далее веса обновляются с учетом направления градиента, но при этом сохраняются сопряженность и перпендикулярность к предыдущим направлениям.
- Процесс продолжается до достижения определенного условия остановки.
Метод сопряженных градиентов широко применяется в различных областях, таких как оптимизация функций, обработка изображений, машинное обучение и другие. Его преимущества включают высокую скорость сходимости и эффективное использование ресурсов вычислительной системы.
Примеры использования методов
Для нахождения минимума кривой существует несколько основных подходов и методов. Рассмотрим несколько примеров использования этих методов:
1. Метод градиентного спуска
Представим, что у нас есть функция, которая описывает кривую, и мы хотим найти минимум этой функции. Метод градиентного спуска позволяет это сделать. Он основывается на использовании градиента функции, который указывает направление наискорейшего возрастания функции. Метод градиентного спуска состоит в последовательном переходе вдоль градиента функции к точке минимума.
Пример использования:
Пусть у нас есть функция f(x) = x^2 + 2x + 1. Используя метод градиентного спуска, мы можем найти минимум этой функции, который находится в точке x = -1. Для этого мы вычисляем градиент функции в точке x, и последовательно делаем шаги вдоль этого градиента до достижения минимума.
2. Метод Ньютона
Метод Ньютона является одним из наиболее эффективных методов нахождения минимума кривой. Он основывается на использовании аппроксимации кривой с помощью касательной в точке. Метод Ньютона позволяет находить минимум функции быстрее, чем метод градиентного спуска, но требует вычисления вторых производных функции.
Пример использования:
Пусть у нас есть функция f(x) = x^2 + 2x + 1. Используя метод Ньютона, мы можем найти минимум этой функции. Для этого мы начинаем с некоторого начального приближения x_0, вычисляем значение функции в этой точке и значение ее производной. Затем мы находим касательную к графику функции в этой точке и переходим к ее корню, который и является минимумом функции.
3. Метод отжига
Метод отжига является вероятностным алгоритмом оптимизации, который используется для нахождения минимума кривой. Он основывается на имитации процесса отжига в металлургии. Метод отжига позволяет искать минимум функции путем выбора новой точки, основываясь на вероятности перехода в новую точку, которая зависит от изменения значения функции и текущей температуры.
Пример использования:
Пусть у нас есть функция f(x) = x^2 + 2x + 1. Используя метод отжига, мы можем найти минимум этой функции. Для этого мы начинаем с некоторого случайного приближения x_0, затем выбираем новую точку x_1 с помощью случайного сдвига от текущей точки. Если значение функции в новой точке меньше, чем в текущей, то мы переходим в нее. Если же значение функции больше, мы переходим в новую точку с вероятностью, которая зависит от значения функции и текущей температуры.