Графы - это мощный инструмент для представления и анализа сложных структур и взаимосвязей между объектами. В различных областях, таких как компьютерная наука, экономика и социология, графы широко используются для моделирования сложных систем и решения различных задач. В графе вершины представляют собой объекты, а ребра - связи между ними.
Одной из основных задач при работе с графами является поиск вершин. Когда граф становится очень большим и сложным, поиск вершин становится сложной задачей, требующей эффективных подходов и алгоритмов. Существуют различные методы поиска вершин графа, которые позволяют находить узлы в графической структуре.
Один из наиболее популярных методов поиска вершин - поиск в ширину. Этот метод основан на идее обхода графа по слоям, начиная с определенной вершины. Поиск в ширину находит все вершины, достижимые из стартовой вершины, и сохраняет порядок, в котором они были обнаружены. Поиск в ширину обычно используется для нахождения кратчайшего пути между двумя вершинами графа.
Другим распространенным методом поиска вершин является поиск в глубину. В отличие от поиска в ширину, этот метод исследует путь вглубь графа, пока не встретит тупиковую ситуацию. Затем алгоритм возвращается назад и исследует другие возможные пути. Поиск в глубину может быть использован для поиска циклов в графе, проверки связности графа и других задач.
Методы поиска вершин графа
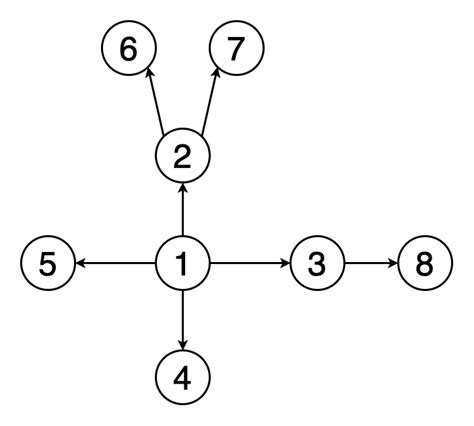
1. Поиск в глубину (Depth-First Search, DFS)
DFS - один из основных методов поиска в графе, который позволяет обойти все вершины в глубину, начиная с заданной вершины. Алгоритм DFS рекурсивно переходит в каждую не посещенную вершину и продолжает обход до тех пор, пока не достигнет конца ветви.
2. Поиск в ширину (Breadth-First Search, BFS)
BFS - метод поиска, который работает по принципу обхода графа в ширину. Алгоритм BFS начинает с заданной вершины и посещает все соседние вершины. Затем он переходит ко второму уровню соседних вершин и так далее, пока не будут обработаны все вершины.
3. Поиск с использованием эвристик
Для более эффективного поиска в графе могут применяться различные эвристические подходы, основанные на предположениях о структуре графа. Например, алгоритм A* использует эвристическую функцию для оценки стоимости достижения данной вершины из начальной. Такие методы позволяют сократить количество вершин, которые необходимо обработать в процессе поиска.
Методы поиска вершин графа являются важным инструментом в решении различных задач, связанных с анализом данных и оптимизацией процессов.
Поиск в глубину

Алгоритм поиска в глубину применяется во многих областях, включая графические структуры данных, поиск пути в лабиринтах, анализ компонент связности графа и др.
Процесс поиска в глубину основан на использовании стека для хранения посещенных вершин. Алгоритм начинает с выбранной стартовой вершины и помещает ее в стек. Затем он продолжает извлекать вершины из стека, посещать их и помещать связанные с ними вершины в стек. Этот процесс продолжается до тех пор, пока стек не станет пустым, что означает, что все вершины были посещены.
Важной частью алгоритма DFS является отметка вершин как посещенных и правильная обработка обратного ребра. При обнаружении обратного ребра, алгоритм должен корректно перейти к следующей не посещенной вершине и продолжить итерацию.
Преимуществом алгоритма DFS является его простота реализации и эффективность в поиске внутри связных компонентов. Однако алгоритм не гарантирует нахождение кратчайшего пути или оптимального решения.
| Преимущества | Недостатки |
|---|---|
| Простота реализации | Не гарантирует нахождение кратчайшего пути |
| Эффективность в поиске внутри связных компонентов | Не гарантирует нахождение оптимального решения |
Поиск в ширину
Преимуществом алгоритма BFS является то, что он гарантирует, что наименее удаленные вершины будут обработаны первыми. Это полезно, например, при поиске кратчайшего пути между двумя вершинами графа, так как BFS обрабатывает узлы в порядке их удаленности от начальной вершины.
Алгоритм BFS может быть реализован с использованием очереди и набора посещенных вершин. Посещенные вершины помечаются, чтобы избежать повторных переходов. Кроме того, BFS можно применять для определения связанных компонентов графа, поиска в ширину в задачах о графе, таких как нахождение минимального остовного дерева или проверка на наличие циклов.
Алгоритм Дейкстры
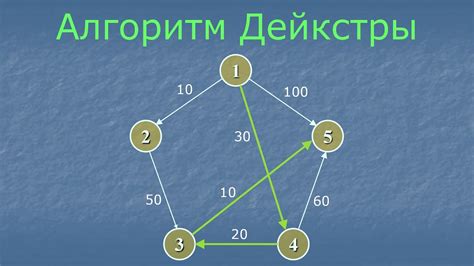
Основная идея алгоритма состоит в построении дерева кратчайших путей от заданной начальной вершины ко всем остальным вершинам графа. Для этого алгоритм использует жадный подход, выбирая на каждом шаге вершину с наименьшим весом и добавляя ее к дереву. Таким образом, на каждой итерации расстояние до всех остальных вершин уточняется.
Алгоритм Дейкстры можно представить в виде следующих шагов:
- Инициализировать начальную вершину и установить для всех остальных вершин бесконечное расстояние.
- Пометить начальную вершину как текущую и ее расстояние как 0.
- Для каждой смежной вершины текущей вершины вычислить временное расстояние с учетом веса ребра.
- Если временное расстояние меньше текущего расстояния до вершины, обновить текущее расстояние.
- Пометить текущую вершину как пройденную.
- Выбрать следующую непомеченную вершину с наименьшим расстоянием и сделать ее текущей.
- Повторить шаги 3-6, пока все вершины не будут пройдены.
После выполнения алгоритма Дейкстры можно получить кратчайший путь к любой вершине, следуя от начальной вершины до соответствующей вершины и сохраняя пройденные ребра.
Алгоритм Прима

Основная идея алгоритма Прима заключается в следующем:
- Выбирается произвольная вершина графа и помечается.
- На каждой итерации алгоритма выбирается ребро минимального веса, исходящее из уже помеченных вершин и ведущее к непомеченной вершине.
- Выбранная вершина помечается, и процесс повторяется до тех пор, пока все вершины графа не будут помечены.
В результате работы алгоритма Прима получается минимальное остовное дерево, которое содержит все вершины исходного графа и имеет наименьшую суммарную длину ребер.
Алгоритм Прима широко применяется в различных областях, где необходимо находить минимальные пути, такие как телекоммуникации, транспортные системы, вычислительная биология и другие.
Алгоритм Крускала
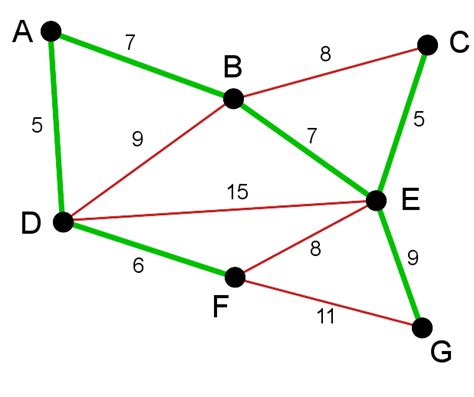
Идея алгоритма заключается в том, чтобы начать с пустого дерева и последовательно добавлять к нему ребра из исходного графа, выбирая каждый раз ребро минимального веса, которое не создаст цикл. Алгоритм продолжает добавлять ребра до тех пор, пока все вершины не станут связанными или не останется доступных ребер.
Для реализации алгоритма Крускала необходимо выполнить следующие шаги:
- Отсортировать все ребра графа в порядке возрастания их весов.
- Инициализировать пустое остовное дерево.
- Для каждого ребра из отсортированного списка:
- Если добавление ребра не создаст цикл в остовном дереве, добавить его в дерево.
- В противном случае, пропустить это ребро и перейти к следующему.
Алгоритм Крускала эффективен и прост в реализации. Он позволяет найти минимальный остовный граф исходного графа за время O(E log E), где E - количество ребер в графе.
Конечный результат работы алгоритма - минимальное остовное дерево, которое содержит только необходимые ребра для связи всех вершин. Это может быть полезно, например, при поиске оптимального маршрута в транспортных сетях или при планировании распределения ресурсов.
Алгоритм Флойда-Уоршелла
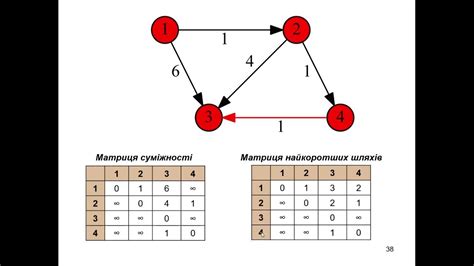
Основная идея алгоритма заключается в том, чтобы построить таблицу размером N x N, где N - количество вершин в графе. Значение в ячейке (i, j) этой таблицы будет представлять собой длину кратчайшего пути от вершины i до вершины j.
Алгоритм Флойда-Уоршелла выполняется за O(N^3) времени, где N - количество вершин в графе. Он проходит через граф несколько раз, обновляя значения ячеек таблицы с использованием промежуточных вершин. Каждый проход алгоритма уменьшает количество вершин, для которых уже найдены кратчайшие пути, и поэтому на каждом следующем проходе обновляется больше значений ячеек таблицы.
Алгоритм Флойда-Уоршелла также может использоваться для обнаружения отрицательных циклов в графе. Если на диагонали таблицы найдется отрицательное значение, это будет означать, что в графе есть отрицательный цикл.
Алгоритм Флойда-Уоршелла широко применяется в различных областях, включая транспортную логистику, телекоммуникационные сети и графовые базы данных.
Алгоритм Беллмана-Форда

Основная идея алгоритма заключается в том, что он последовательно рассчитывает приближенные значения кратчайших путей от исходной вершины до всех остальных вершин графа. Алгоритм начинает с предположения, что самый короткий путь до каждой вершины состоит из нулевых ребер и имеет бесконечно большую стоимость. Затем, на каждой итерации, алгоритм "релаксирует" каждое ребро графа, чтобы улучшить текущую оценку кратчайшего пути до вершины.
Алгоритм Беллмана-Форда может корректно работать с графами, содержащими ребра отрицательного веса, однако при условии отсутствия циклов отрицательной длины. Если в графе присутствуют циклы отрицательной длины, алгоритм Беллмана-Форда определит это и сообщит о наличии отрицательного цикла.
Одним из примеров применения алгоритма Беллмана-Форда является задача поиска кратчайшего пути в графе с отрицательными весами. Также алгоритм может быть использован для определения наличия отрицательных циклов в графе и решения других задач, связанных с поиском кратчайших путей.
В целом, алгоритм Беллмана-Форда является эффективным решением для нахождения кратчайших путей в графе с отрицательными ребрами, однако его время работы зависит от количества вершин и ребер графа и в худшем случае составляет O(V * E), где V - количество вершин, а E - количество ребер.
Алгоритм A*
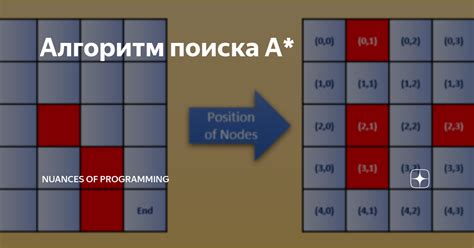
Основная идея алгоритма A* состоит в том, чтобы найти путь от начального узла к целевому узлу, минимизируя функцию стоимости, которая представляет собой сумму стоимости пути от начального узла до текущего узла и эвристической оценки стоимости до целевого узла.
Эвристическая функция, или оценочная функция, используется для приближенного оценивания стоимости пути от текущего узла до целевого узла. Идеальная эвристическая функция должна быть допустимой, то есть не переоценивать стоимость пути. Вершины с наименьшим значением эвристической функции рассматриваются в первую очередь.
A* алгоритм начинает с начального узла и итеративно ищет путь, добавляя смежные узлы в открытый список. Каждый раз, когда алгоритм перемещается в новый узел, он пересчитывает значение стоимости пути до этого узла и эвристическую функцию для оценки стоимости до целевого узла. Если оценка стоимости пути до текущего узла меньше, чем оценка стоимости пути до этого узла из ранее посещенных узлов, то новый путь становится более предпочтительным и текущий узел помечается как предшественник нового пути.
Алгоритм продолжает итерацию до тех пор, пока не будет найден путь до целевого узла или пока открытый список не станет пустым. Если путь до целевого узла был найден, то можно восстановить сам путь, используя предшественников, которые были помечены на протяжении поиска. Таким образом, алгоритм A* позволяет эффективно находить оптимальные пути в графе и широко применяется в различных областях, таких как робототехника, компьютерные игры и планирование маршрутов.