Нормальность распределения данных является важным предположением для многих статистических тестов и анализов. SPSS (Statistical Package for the Social Sciences) является популярным программным обеспечением для анализа данных, которое предоставляет возможность проверить нормальность распределения.
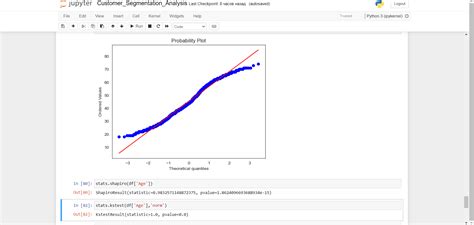
Существует несколько методов, которые можно использовать для проверки нормальности распределения в SPSS. Один из наиболее распространенных методов - это графическая проверка с помощью Q-Q графика (квантиль-квантиль графика). Q-Q график сравнивает квантили нормальной выборки с квантилями исследуемой выборки и позволяет определить, насколько хорошо данные соответствуют нормальному распределению.
В SPSS для построения Q-Q графика необходимо выполнить следующие шаги: сначала загрузить данные в программу, затем выбрать меню «Анализ», далее «Оценка критериев нормальности…» и, наконец, выбрать переменную для анализа. После выполнения этих шагов SPSS построит Q-Q график, который можно проанализировать для определения нормальности данных.
Методы проверки нормальности распределения в SPSS
SPSS (Statistical Package for the Social Sciences) представляет собой мощный инструмент для анализа данных, который позволяет проводить различные статистические тесты, включая проверку нормальности распределения.
Нормальное распределение является одним из основных предположений, используемых во многих статистических тестах. Проверка нормальности распределения важна, поскольку многие статистические методы основаны на предположении о нормальности данных. Если данные не имеют нормальное распределение, возможны искажения результатов статистического анализа.
В SPSS существует несколько методов для проверки нормальности распределения данных:
- Критерий Шапиро-Уилка. Данный критерий является одним из наиболее часто используемых для проверки нормальности распределения. Он основан на сравнении фактического распределения с теоретическим нормальным распределением. Результатом является значение p - вероятность того, что данные распределены ненормально. Если значение p меньше выбранного уровня значимости, то гипотеза о нормальности распределения отвергается.
- Критерий Колмогорова-Смирнова. Данный критерий также используется для проверки нормальности распределения. Он основан на сравнении эмпирической функции распределения с функцией распределения нормального распределения. Результатом является значение K-S - максимальное отклонение между двумя функциями. Если значение K-S больше критического значения, то гипотеза о нормальности распределения отвергается.
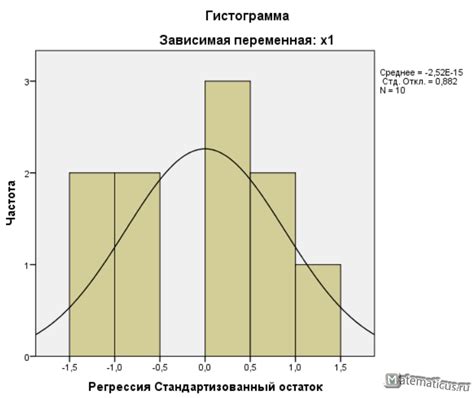
- Графический анализ. В SPSS также имеются инструменты для графической проверки нормальности распределения. Например, можно построить гистограмму и график квантиль-квантиль (Q-Q plot), чтобы визуально оценить соответствие данных нормальному распределению. Если значения на графике отклоняются от линии, соответствующей нормальному распределению, это может указывать на нарушение нормальности.
Проверка нормальности распределения в SPSS является важным шагом при анализе данных и позволяет определить, можно ли применять статистические методы, основанные на предположении о нормальности. Учитывая важность проверки нормальности, SPSS предоставляет несколько методов для проведения данного анализа.
Тест Шапиро-Уилка: инструкция и применение
Для выполнения теста Шапиро-Уилка в программе SPSS следуйте следующим шагам:
- Откройте набор данных в SPSS.
- Выберите переменную, распределение которой необходимо проверить на нормальность.
- Откройте меню "Анализ" и выберите пункт "Оценка распределения" - "Проверка нормальности" - "Одновыборочный Шапиро-Уилк".
- Перетащите выбранную переменную в поле "Переменные".
- Установите желаемый уровень значимости в поле "Уровень значимости". Обычно используются значения 0,05 или 0,01.
- Нажмите кнопку "ОК", чтобы выполнить тест Шапиро-Уилка.
В результате выполнения теста Шапиро-Уилка в SPSS вы получите следующую информацию:
| Показатель | Описание |
|---|---|
| W | Статистика теста Шапиро-Уилка |
| p-значение | Вероятность того, что наблюдаемые данные могли быть получены из нормального распределения |
Тест Шапиро-Уилка является одним из наиболее распространенных статистических тестов для проверки нормальности распределения данных. Он широко используется во многих областях, таких как экономика, психология, биология и др.
Колмогоров-Смирнов тест: измерение нормальности распределения

Применение Колмогоров-Смирнов теста в SPSS позволяет проверить гипотезу о нормальности данных и оценить уровень значимости этой гипотезы. Если значение уровня значимости меньше выбранного критического уровня, гипотеза о нормальности данных будет отвергнута.
Для проведения Колмогоров-Смирнов теста в SPSS необходимо выполнить следующие шаги:
- Открыть файл с данными в SPSS.
- Выбрать меню "Анализ" (Analysis), затем "Не параметрические проверки" (Nonparametric Tests) и "Одновыборочный Колмогоров-Смирнов тест" (One-Sample Kolmogorov-Smirnov Test).
- Выбрать переменную, для которой хотите проверить нормальность распределения, и добавить ее в поле "Переменные" (Variables).
- Нажать кнопку "ОК" (OK), чтобы выполнить тест.
- В результате теста SPSS выдаст значение статистической величины Колмогорова-Смирнова (D) и соответствующее значение уровня значимости (p-value).
Интерпретация результатов Колмогоров-Смирнов теста зависит от выбранного уровня значимости. Если p-value больше уровня значимости, то гипотеза о нормальности данных не может быть отвергнута. Если же p-value меньше уровня значимости, то можно считать, что данные распределены не нормально.
Важно отметить, что Колмогоров-Смирнов тест чувствителен к объему выборки. Поэтому при маленьком объеме выборки может быть сложно добиться статистической значимости при сравнении с идеальным нормальным распределением.
Графические методы проверки нормальности в SPSS: примеры использования
1. QQ-график
QQ-график (график квантилей-квантилей) является одним из наиболее распространенных графических методов проверки нормальности в SPSS. Он позволяет визуально сравнить распределение данных с теоретическим нормальным распределением. Для построения QQ-графика в SPSS необходимо выполнить следующие шаги:
- Выберите вкладку "Graphs" в верхней панели меню SPSS.
- Перейдите к разделу "Legacy Dialogs" и выберите "QQ Plot".
- В окне "QQ Plot", выберите переменные, для которых хотите построить QQ-график, и нажмите "OK".
Пример использования: Допустим, у нас есть переменная "Age", которая содержит возраст субъектов исследования. Мы хотим проверить, являются ли эти данные нормально распределенными. В SPSS мы выбираем переменную "Age", следуем указанным выше шагам и получаем QQ-график, который позволяет нам визуально сравнить распределение возраста с теоретическим нормальным распределением.
2. Гистограмма с кривой нормального распределения
Гистограмма с кривой нормального распределения является еще одним графическим методом проверки нормальности в SPSS. Он позволяет визуально сравнить распределение данных с предполагаемым нормальным распределением и оценить их соответствие. Для построения гистограммы с кривой нормального распределения в SPSS необходимо выполнить следующие шаги:
- Выберите вкладку "Graphs" в верхней панели меню SPSS.
- Перейдите к разделу "Legacy Dialogs" и выберите "Histogram".
- В окне "Histogram", выберите переменную, для которой хотите построить гистограмму с кривой нормального распределения, и нажмите "OK".
Пример использования: Предположим, у нас есть переменная "Height", которая содержит рост субъектов исследования. Мы хотим проверить, являются ли эти данные нормально распределенными. В SPSS мы выбираем переменную "Height", следуем указанным выше шагам и получаем гистограмму с кривой нормального распределения, которая позволяет нам оценить соответствие распределения роста предполагаемому нормальному распределению.
3. КРС-график и график Лоренца
КРС-график (квантиль-квантиль-сглаженный) и график Лоренца позволяют проверить нормальность распределения данных, основываясь на сравнении ожидаемых квантилей с реальными квантилями. Для построения КРС-графика и графика Лоренца в SPSS необходимо выполнить следующие шаги:
- Выберите вкладку "Graphs" в верхней панели меню SPSS.
- Перейдите к разделу "Legacy Dialogs" и выберите "Scatter/Dot".
- В окне "Scatter/Dot", выберите переменные, для которых хотите построить КРС-график и график Лоренца, и нажмите "OK".
Пример использования: Предположим, у нас есть переменная "Income", которая содержит информацию о доходе субъектов исследования. Мы хотим проверить, являются ли эти данные нормально распределенными. В SPSS мы выбираем переменную "Income", следуем указанным выше шагам и получаем КРС-график и график Лоренца, которые позволяют нам визуально сравнить ожидаемые квантили дохода с реальными квантилями и оценить соответствие распределения дохода теоретическому нормальному распределению.
Другие статистические тесты: альтернативные методы проверки нормальности

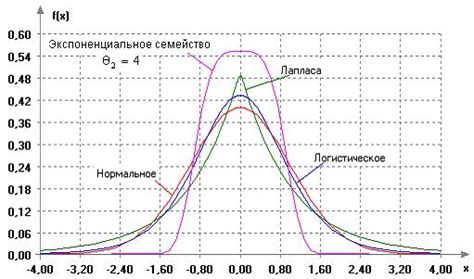
Помимо классических методов проверки нормальности распределения, таких как Шапиро-Уилка, тест Колмогорова-Смирнова и Андерсона-Дарлинга, существуют и другие статистические тесты, которые могут быть использованы для оценки нормальности данных.
Некоторые из них включают следующие:
| Название теста | Описание |
|---|---|
| Тест Лиллиефорса | Позволяет проверять гипотезу о нормальности распределения на основе построения ряда абсолютных значений разности между эмпирическими и теоретическими функциями распределения. В случае нормального распределения разности будут распределены равномерно. |
| Тест Жарка-Бера | Основан на оценке среднеквадратического отклонения (СКО) остатков регрессионной модели и проверке его нормальности. Чем ближе СКО остатков к теоретическому значению, тем более нормальными считаются данные. |
| Тест Крамера-фон Мизеса | Используется для проверки нормальности распределения на основе вычисления квадратов отклонений между эмпирической и теоретической функцией распределения. На основе полученного значения статистики сравнивают с критическими значениями, чтобы принять или отвергнуть гипотезу о нормальности. |
| Тест Колмогорова-Либмана-Лоу | Оценивает сходство между эмпирической функцией распределения и гипотетической нормальной функцией. На основе разницы между двумя функциями вычисляется статистика, которая сравнивается с критическими значениями для проверки нормальности. |
Важно отметить, что каждый из этих тестов имеет свои особенности и предпосылки, которые необходимо учитывать при их применении. Лучшим подходом будет использование нескольких тестов одновременно для более надежной оценки нормальности данных.