Поиск производной двух переменных является важной задачей в математике и физике. Методы и правила, которые можно применять при решении таких задач, помогают выявить закономерности и характер изменения функций. Такие знания широко применяются в различных областях, включая экономику, инженерию и науку.
Основные методы поиска производной двух переменных включают в себя парциальные производные, правило производной сложной функции, правила производных элементарных функций и методы дифференцирования неявных функций. Эти методы помогают найти производную функции от двух переменных по отношению к одной или обеим переменным.
При поиске производной двух переменных необходимо учитывать также правила дифференцирования сложной функции, цепное правило дифференцирования и правила производных элементарных функций. Благодаря этим правилам можно находить значения производных сложных функций и функций, содержащих элементарные функции, такие как синус, косинус, степенная функция и логарифм.
Поиск производной двух переменных является важным инструментом для изучения и анализа функций. Он позволяет определить экстремумы функций, траектории движения, скорости изменения и многое другое. Знание методов и правил поиска производной двух переменных позволяет эффективно решать задачи в различных областях науки и техники.
Определение производной и ее значения

Значение производной в заданной точке позволяет узнать, как функция меняется в данной точке и в определенном направлении. Если значение производной положительно, это говорит о том, что функция возрастает в данной точке и в данном направлении. Если значение производной отрицательно, это означает, что функция убывает в данной точке и в данном направлении. Если значение производной равно нулю, то это указывает на точку экстремума функции.
Для нахождения производной функции двух переменных необходимо использовать соответствующие методы дифференцирования, такие как частные производные, правило дифференцирования сложных функций и правило дифференцирования произведения функций. Каждый из этих методов имеет свою формулу и условия применения.
| Метод | Формула | Условия применения |
|---|---|---|
| Частные производные | ∂f/∂x, ∂f/∂y | Функция должна быть дифференцируемой по каждой переменной |
| Правило дифференцирования сложных функций | d(f(g(x,y)))/dx = (∂f/∂x)(∂g/∂x) + (∂f/∂y)(∂g/∂y) | Функции f и g должны быть дифференцируемыми по каждой переменной |
| Правило дифференцирования произведения функций | d(f(x,y)g(x,y))/dx = g(x,y)(∂f/∂x) + f(x,y)(∂g/∂x) | Функции f и g должны быть дифференцируемыми по каждой переменной |
Изучение и применение этих методов позволит эффективно находить производные функций двух переменных и анализировать их изменение в заданных точках и направлениях. Это важный инструмент для решения задач оптимизации и моделирования в различных областях науки и техники.
Значение производной в точке и её интерпретация
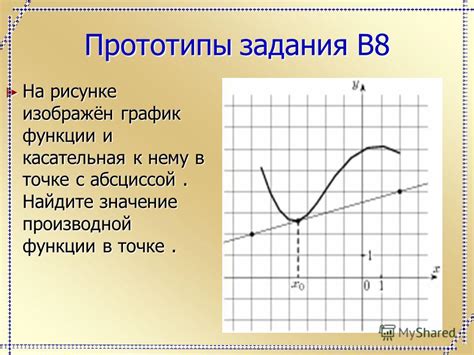
Если значение производной положительно, то это означает, что функция возрастает в данной точке. Если значение производной отрицательно, то функция убывает. А если значение производной равно нулю, то это говорит о наличии экстремума – либо минимума, либо максимума в этой точке.
Интерпретация значения производной помогает нам понять поведение функции в окрестности данной точки. Если значение производной стремится к положительному бесконечности, то функция возрастает; если производная стремится к отрицательному бесконечности, то функция убывает. Если производная стремится к конечному числу, то функция является ограниченной в данной точке.
Важность поиска производной в задачах математического анализа

Производная находит широкое применение в различных областях, таких как физика, экономика, биология и другие науки. В задачах механики производная позволяет определить мгновенную скорость движения объекта, а также его ускорение. В экономике производная используется для определения эластичности спроса и предложения. В биологии производная помогает понять динамику популяций и изменение во времени различных параметров организма.
Поиск производной позволяет также определить экстремумы функции, то есть ее максимумы и минимумы. Это важно для определения оптимальных значений в различных задачах оптимизации, например, при поиске максимальной прибыли или минимальных затрат.
Основные методы поиска производной включают использование правил дифференцирования, аналитическое дифференцирование, численные методы и символьные методы. Каждый из этих методов имеет свои преимущества и ограничения, и выбор метода зависит от конкретной задачи и доступных ресурсов.
Таким образом, поиск производной является важным инструментом математического анализа, который применяется для решения различных задач. Понимание и использование этого метода позволяет получить лучшие результаты и более глубокое понимание функций и их свойств.
Методы поиска производной двух переменных

Существуют различные методы поиска производной двух переменных, каждый из которых обладает своими особенностями и применяется в разных ситуациях. Некоторые из наиболее распространенных методов включают:
- Метод дифференцирования по переменной. Этот метод основывается на правиле дифференцирования функции, которая содержит две переменные. С помощью цепного правила и правила дифференцирования элементарных функций, можно найти производную по каждой переменной.
- Метод частных производных. Этот метод позволяет найти производные функции, содержащей несколько переменных, по каждой переменной по отдельности. Частная производная показывает скорость изменения функции только по одной из переменных, при условии, что остальные переменные остаются постоянными.
- Метод неявной дифференциации. Этот метод применяется, когда функция задана неявно в виде уравнения. Метод основывается на неявном дифференцировании уравнения и позволяет найти производные по каждой переменной.
- Метод преобразования переменных. Этот метод заключается в замене переменных функции, чтобы упростить процесс нахождения производной. Преобразуя переменные, можно перейти к функции с одной переменной или снизить сложность дифференцирования.
Выбор метода зависит от вида задачи и доступных инструментов. Знание различных методов поиска производной двух переменных позволяет эффективно анализировать функции и применять их в решении задач из различных областей науки и техники.
Метод частных производных

Для использования метода частных производных необходимо знать, что производная функции по одной переменной является частной производной функции по этой переменной. В математической записи эту идею можно выразить так:
∂f/∂x = ∂f/∂y = … = ∂f/∂xn
Здесь ∂f/∂x, ∂f/∂y, …, ∂f/∂xn обозначают частные производные функции f по переменным x, y, …, xn соответственно.
Для поиска частных производных функции двух переменных можно использовать два основных метода: метод дифференциалов и метод частных изменений. Оба метода позволяют находить производные функции по отдельным переменным, не задействуя другие переменные.
Метод частных производных широко применяется в физике, экономике, инженерии и других областях науки, где встречаются функции нескольких переменных. С его помощью можно изучать зависимости между различными параметрами и находить экстремумы функций двух переменных.
Метод дифференцирования по направлению

Чтобы применить метод дифференцирования по направлению, необходимо знать градиент функции и направляющий вектор. Градиент функции – это вектор, состоящий из частных производных функции. Направляющий вектор задает направление, в котором нужно искать производную функции.
Для определения производной функции в заданной точке в направлении вектора следует использовать следующую формулу:
Df(P, V) = ∇f(P)·V
где:
- Df(P, V) – производная функции в точке P в направлении вектора V;
- ∇f(P) – градиент функции в точке P;
- V – направляющий вектор.
Поиск производной по направлению является полезным инструментом для оптимизации функций и может быть использован в различных областях, таких как математика, физика, экономика, и т.д.
Метод линеаризации функции

Для применения метода линеаризации функции сначала выбирается точка, в которой необходимо найти производную. Затем проводится линейная аппроксимация функции в окрестности этой точки. Линейная аппроксимация основывается на использовании линейной формы функции.
Для линейной аппроксимации функции вблизи точки (x0, y0) используется следующая формула:
f(x, y) ≈ f(x0, y0) + fx(x0, y0)(x - x0) + fy(x0, y0)(y - y0)
где f(x, y) – исходная функция, f(x0, y0) – значение функции в точке (x0, y0), fx(x0, y0) – частная производная функции по x, рассчитанная в точке (x0, y0), fy(x0, y0) – частная производная функции по y, рассчитанная в точке (x0, y0).
После проведения линейной аппроксимации получается линейное выражение, которое затем используется для нахождения производной в точке (x0, y0). Производные fx(x0, y0) и fy(x0, y0) могут быть найдены с использованием известных правил дифференцирования.
Метод линеаризации функции является приближенным методом, но он позволяет получить достаточно точное значение производной в окрестности заданной точки. Он широко применяется в различных областях науки и техники, где требуется аппроксимация и дифференцирование функций от двух переменных.