Точка пересечения трех сфер – это место, где все три сферы пересекаются в пространстве. На первый взгляд может показаться, что посчитать координаты этой точки достаточно сложно, но на самом деле существует несколько методов, которые помогут вам решить эту задачу. В этой статье мы подробно рассмотрим эти методы и предоставим несколько примеров для лучшего понимания.
Первый метод основан на использовании теоремы о трех сферах. Суть этого метода заключается в том, что для нахождения точки пересечения трех сфер нужно решить систему уравнений, полученную из уравнений сфер. Затем координаты точки пересечения можно найти, решив эту систему. Данный метод требует знания алгебры и математического анализа, поэтому его применение может быть сложным для тех, кто не имеет соответствующей подготовки.
Второй метод основан на использовании геометрической интерпретации трех сфер. В этом методе необходимо провести перпендикуляры к плоскостям, определяемым сферами, и найти их точку пересечения. Затем можно найти координаты точки пересечения, используя геометрические свойства и соотношения. Данный метод может быть проще в использовании, но также требует достаточного уровня понимания геометрии и способности проводить точные измерения.
Третий метод – это использование специализированного программного обеспечения, такого как 3D-моделирование или математические пакеты. Эти программы позволяют визуализировать сферы и точку пересечения, а также автоматически находить ее координаты. Такой подход может быть полезен для тех, кто предпочитает работать с готовыми инструментами и не хочет тратить время на решение уравнений или проведение измерений вручную.
В завершение, мы рекомендуем вам выбрать метод, который лучше всего соответствует вашим навыкам и требованиям, чтобы найти точку пересечения трех сфер с наименьшими усилиями. Далее приведем несколько примеров, которые помогут вам лучше понять и применить описанные методы в реальной жизни.
Точка пересечения трех сфер
Найдите точку пересечения трех сфер, используя следующие шаги:
- Задайте параметры для каждой из сфер, такие как радиус, центр и коэффициенты смещения.
- Решите систему уравнений, представляющую пересечение трех сфер. Для этого составьте уравнения, представляющие сферы и приравняйте их друг к другу.
- Решите систему уравнений методом подстановки или методом Гаусса. Полученное решение будет точкой пересечения трех сфер.
Пример:
- Сфера 1: радиус = 5, центр = (2, 3, 4)
- Сфера 2: радиус = 4, центр = (1, 2, 3)
- Сфера 3: радиус = 3, центр = (0, 1, 2)
Уравнения для сфер могут быть представлены следующим образом:
- Сфера 1: (x-2)^2 + (y-3)^2 + (z-4)^2 = 5^2
- Сфера 2: (x-1)^2 + (y-2)^2 + (z-3)^2 = 4^2
- Сфера 3: (x-0)^2 + (y-1)^2 + (z-2)^2 = 3^2
Используя метод Гаусса, мы можем решить эту систему уравнений и найти точку пересечения трех сфер.
Как найти точку пересечения трех сфер
Пересечение трех сфер может быть полезным инструментом при решении различных задач в геометрии и инженерии. Найти точку пересечения трех сфер можно с помощью нескольких шагов, используя известные параметры каждой сферы.
- Установите координаты центров трех сфер и их радиусы.
- Решите систему уравнений, состоящую из уравнений сфер и выражающих их параметров.
- Найдите точку пересечения сфер, решив систему уравнений. Если система уравнений не имеет решений, то сферы не пересекаются.
Чтобы найти точку пересечения сферы с плоскостью, можно использовать метод попарного пересечения сфер. Пересечение двух сфер дает окружность, а пересечение трех сфер определяет точку пересечения.
Если вы программируете на языке Python, можно воспользоваться библиотекой numpy для решения системы уравнений и matplotlib для визуализации результатов.
Используя методы геометрии и алгебры, можно найти точку пересечения трех сфер и применить ее в различных областях, включая компьютерную графику, робототехнику и трехмерное моделирование.
Математические основы

Для начала, введем уравнения трех сфер:
Сфера 1: (x - x1)2 + (y - y1)2 + (z - z1)2 = r12
Сфера 2: (x - x2)2 + (y - y2)2 + (z - z2)2 = r22
Сфера 3: (x - x3)2 + (y - y3)2 + (z - z3)2 = r32
Затем, приведем уравнения к общему виду:
Сфера 1: x2 + y2 + z2 - 2x1x - 2y1y - 2z1z + x12 + y12 + z12 - r12 = 0
Сфера 2: x2 + y2 + z2 - 2x2x - 2y2y - 2z2z + x22 + y22 + z22 - r22 = 0
Сфера 3: x2 + y2 + z2 - 2x3x - 2y3y - 2z3z + x32 + y32 + z32 - r32 = 0
Далее, используя метод пересечения сфер, мы получаем систему уравнений, решая которую можно найти координаты точки пересечения:
Система уравнений:
x2 + y2 + z2 - 2x1x - 2y1y - 2z1z + x12 + y12 + z12 - r12 = 0
x2 + y2 + z2 - 2x2x - 2y2y - 2z2z + x22 + y22 + z22 - r22 = 0
x2 + y2 + z2 - 2x3x - 2y3y - 2z3z + x32 + y32 + z32 - r32 = 0
Для решения системы уравнений можно использовать различные методы, такие как метод Гаусса или метод Ньютона. Решив систему, мы найдем значения переменных x, y и z, которые и будут координатами точки пересечения трех сфер.
Алгоритм поиска
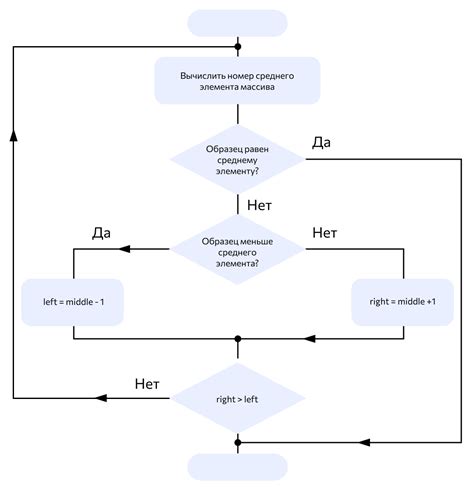
При поиске точки пересечения трех сфер необходимо следовать следующему алгоритму:
- Найдите центры сфер (координаты x, y, z) и радиусы (r) каждой из трех сфер.
- Создайте систему уравнений для каждой пары сфер. Уравнение для пары сфер будет иметь вид (x - x1)2 + (y - y1)2 + (z - z1)2 = r12, где (x1, y1, z1) - координаты центра первой сферы, r1 - радиус первой сферы.
- Решите систему уравнений для первой и второй сферы, используя методы решения квадратных уравнений.
- Подставьте найденные значения координат (x, y, z) в уравнение третьей сферы и решите полученное уравнение.
- Получите координаты точки пересечения трех сфер.
Если решение системы уравнений не существует или является вырожденным, то точка пересечения сфер не существует. Если решение существует, то полученные координаты являются координатами точки пересечения.
Примеры нахождения точки пересечения трех сфер
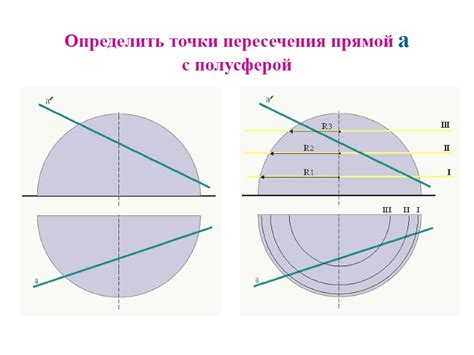
Для нахождения точки пересечения трех сфер потребуется решить систему уравнений. Рассмотрим несколько примеров:
Пример 1:
Даны три сферы с центрами в точках A(1, 2, 3), B(4, 5, 6) и C(7, 8, 9), и радиусами r1=2, r2=3, r3=4. Найдем точку пересечения.
Систему уравнений можно записать следующим образом:
(x - Ax)2 + (y - Ay)2 + (z - Az)2 = r12
(x - Bx)2 + (y - By)2 + (z - Bz)2 = r22
(x - Cx)2 + (y - Cy)2 + (z - Cz)2 = r32
Решение этой системы уравнений даст координаты точки пересечения сфер.
Пример 2:
Даны три сферы с центрами в точках A(-1, 0, 2), B(2, -1, 4) и C(3, 2, 1), и радиусами r1=3, r2=2, r3=4. Найдем точку пересечения.
Аналогично предыдущему примеру, записываем систему уравнений:
(x - Ax)2 + (y - Ay)2 + (z - Az)2 = r12
(x - Bx)2 + (y - By)2 + (z - Bz)2 = r22
(x - Cx)2 + (y - Cy)2 + (z - Cz)2 = r32
Решая систему уравнений, получим координаты точки пересечения сфер.
Пример 3:
Даны три сферы с центрами в точках A(0, 0, 0), B(1, 1, 1) и C(-1, -1, -1), и радиусами r1=1, r2=2, r3=3. Найдем точку пересечения.
Записываем систему уравнений:
(x - Ax)2 + (y - Ay)2 + (z - Az)2 = r12
(x - Bx)2 + (y - By)2 + (z - Bz)2 = r22
(x - Cx)2 + (y - Cy)2 + (z - Cz)2 = r32
Решая систему уравнений, получим координаты точки пересечения трех сфер.
Пример 1

Рассмотрим пример трех сфер с заданными координатами центров и радиусами.
| Сфера 1 | Сфера 2 | Сфера 3 |
|---|---|---|
| Центр: (1, 2, 3) | Центр: (4, 5, 6) | Центр: (7, 8, 9) |
| Радиус: 2 | Радиус: 3 | Радиус: 4 |
Для нахождения точки пересечения трех сфер, воспользуемся алгоритмом трех пересечений.
- Найдем две точки пересечения сфер 1 и 2.
- Используя эти две точки пересечения, найдем две возможные точки пересечения сфер 1 и 3.
- Исключим неправильную точку пересечения, не лежащую на всех трех сферах.
После выполнения этих шагов, мы получим точку пересечения трех сфер.
Пример 2

Для решения задачи нахождения точки пересечения трех сфер можно использовать метод пересечения плоскостей. В данном примере будем использовать систему координат с осями X, Y и Z.
- Зададим координаты центров трех сфер: A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3).
- Найдем расстояния от каждого центра до точки пересечения плоскостей: r1, r2 и r3.
- Найдем нормальные векторы плоскостей, проходящих через каждую из сфер: n1 = (x - x1, y - y1, z - z1), n2 = (x - x2, y - y2, z - z2) и n3 = (x - x3, y - y3, z - z3).
- Найдем уравнения плоскостей, проходящих через каждую из сфер: p1: n1 · (x - x1) + n1 · (y - y1) + n1 · (z - z1) = r1, p2: n2 · (x - x2) + n2 · (y - y2) + n2 · (z - z2) = r2 и p3: n3 · (x - x3) + n3 · (y - y3) + n3 · (z - z3) = r3.
- Решим полученную систему уравнений плоскостей и найдем координаты точки пересечения плоскостей: (x*, y*, z*).
Таким образом, получив координаты точки пересечения плоскостей, мы найдем точку пересечения трех сфер.
Пример 2 поможет наглядно продемонстрировать алгоритм нахождения точки пересечения трех сфер и применить его к конкретной задаче.