Когда мы работаем с числами в программировании, часто возникает необходимость найти количество делителей для определенного числа. Зачастую мы ищем все делители числа, чтобы решить определенную задачу или просто для вычисления математических функций. В Python существует несколько методов, которые позволяют найти число делителей числа и использовать его в своих задачах.

Один из самых простых методов для поиска числа делителей - это перебор всех чисел от 1 до заданного числа. Если число делителей при этом увеличивается на 1, то мы находимся перед следующим делителем. С помощью цикла for и условной конструкции if мы можем реализовать этот механизм и найти количество делителей заданного числа.

Еще один способ - это разложение числа на простые множители. Когда мы разлагаем число на простые множители, мы можем найти делители числа, опираясь на свойства простых чисел. Например, если число имеет множитель 2, то оно делится на 2. Также мы можем использовать формулу, которая позволяет найти число делителей числа на основе количества простых множителей и их степеней.

Поиск числа делителей числа в Python

В Python существует несколько методов для поиска делителей числа. Рассмотрим несколько из них:

num = 10
divisors = []
for i in range(1, num+1):
if num % i == 0:
divisors.append(i)

import math
num = 10
divisors = []
for i in range(1, int(math.sqrt(num))+1):
if num % i == 0:
divisors.append(i)
if i != num // i:
divisors.append(num // i)

num = 10
divisors = [i for i in range(1, num+1) if num % i == 0]

Выбор конкретного метода зависит от требуемой точности, скорости выполнения и контекста задачи. Важно помнить, что некоторые методы могут быть эффективнее для больших чисел, чем другие. В любом случае, поиск делителей числа в Python является важной задачей при работе с числами и может быть полезным инструментом в различных областях программирования.

Методы определения числа делителей

Существует несколько методов определения числа делителей для данного числа.

1. Перебор делителей: этот метод заключается в переборе всех чисел от 1 до заданного числа и проверке, является ли каждое из них делителем данного числа. Если число делителей превышает заданное число, то числу присваивается это значение.

2. Формула для нахождения количества делителей: для определения количества делителей числа можно использовать следующую формулу: если число имеет разложение на простые множители вида p1^a1 * p2^a2 * ... * pn^an, где p1, p2, ..., pn - простые числа, а a1, a2, ..., an - их степени, то количество делителей равно (a1+1)*(a2+1)*...*(an+1).

3. Использование математической функции sqrt: вместо перебора всех чисел до заданного числа можно ограничиться перебором всех чисел до квадратного корня из заданного числа. Если число делителей превышает заданное число, то числу присваивается это значение.

Выбор метода определения числа делителей зависит от требуемой точности и скорости вычислений. Каждый метод имеет свои достоинства и недостатки, и выбор должен основываться на конкретной ситуации и требованиях задачи.

Перебор всех чисел до заданного числа

Для реализации перебора всех чисел до заданного числа можно использовать цикл for. Начиная с числа 1 и до заданного числа, каждое число проверяется на делимость с помощью оператора %. Если остаток от деления равен нулю, то число является делителем.

Пример кода:

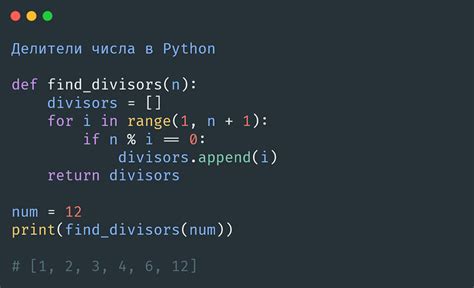
def find_divisors(num):
divisors = []
for i in range(1, num+1):
if num % i == 0:
divisors.append(i)
return divisors
number = 24
result = find_divisors(number)
print(f"Делители числа {number}: {result}")

Результат выполнения программы:

Делители числа 24: [1, 2, 3, 4, 6, 8, 12, 24]

Таким образом, были найдены все делители числа 24 - это числа от 1 до 24, которые делятся на 24 без остатка.

Использование формулы Эйлера

Формула Эйлера позволяет определить количество делителей для натурального числа, основываясь на его разложении на простые множители. Формула может быть полезна при поиске числа делителей в больших числах.

Формула Эйлера утверждает, что если число n представлено в виде произведения простых множителей вида n = p^a * q^b * r^c ... , где p, q, r ... - простые числа, а a, b, c ... - их степени, то количество делителей d(n) будет равно произведению (a+1)*(b+1)*(c+1) ...

Таким образом, формула Эйлера позволяет находить количество делителей числа, опираясь на его разложение на простые множители. Эта формула может быть использована в программировании для эффективного нахождения числа делителей некоторого числа.

Использование функции sqrt

Для использования функции sqrt() необходимо импортировать модуль math, в котором она определена. Для этого используется следующая команда:

• import math

После импорта модуля math, функция sqrt() может быть вызвана, указав число в скобках:

• x = math.sqrt(25)

В данном примере, функция sqrt() вернет значение 5.0, так как квадратный корень числа 25 равен 5.0.

Функцию sqrt() можно использовать для различных задач. Например, для нахождения гипотенузы прямоугольного треугольника по заданным катетам:

• c = math.sqrt(a**2 + b**2)

В данном примере, функция sqrt() используется для вычисления квадратного корня суммы квадратов катетов a и b, где c - гипотенуза треугольника.

Использование функции sqrt() позволяет упростить вычисления в Python и получить точные значения квадратных корней чисел.

Примеры кода для поиска числа делителей

Вот несколько примеров кода на языке Python, которые помогут найти число делителей заданного числа:

def count_divisors(n):
count = 0
for i in range(1, n+1):
if n % i == 0:
count += 1
return count
number = 24
divisors = count_divisors(number)
print(f"Число делителей числа {number}: {divisors}")

def count_divisors(n):
count = 0
sqrt_n = int(n ** 0.5)
for i in range(1, sqrt_n + 1):
if n % i == 0:
count += 2
if sqrt_n ** 2 == n:
count -= 1
return count
number = 24
divisors = count_divisors(number)
print(f"Число делителей числа {number}: {divisors}")

import math
def count_divisors(n):
count = 0
sqrt_n = int(math.sqrt(n))
for i in range(1, sqrt_n + 1):
if n % i == 0:
count += 2
if sqrt_n ** 2 == n:
count -= 1
return count
number = 24
divisors = count_divisors(number)
print(f"Число делителей числа {number}: {divisors}")

Выберите подходящий метод или пример кода в зависимости от ваших потребностей и предпочтений. Помните, что разные методы могут быть эффективными для разных случаев, и вам стоит экспериментировать с разными вариантами.