Окружность - важный геометрический объект, который часто встречается не только в математических задачах, но и в различных областях, таких как физика, инженерия, и дизайн. Важной задачей при работе с окружностями является построение касательной к окружности через заданную точку.
В математике существуют несколько методов для построения такой касательной. Один из самых простых и широко используемых методов - это метод тангенсов. Суть метода заключается в построении прямой, которая проходит через заданную точку и касается окружности в данной точке.
Для построения касательной к окружности через точку с помощью метода тангенсов необходимо знать координаты центра окружности и радиус окружности, а также координаты заданной точки. Используя эти данные, можно определить уравнение прямой, проходящей через заданную точку и центр окружности. Затем, решая систему уравнений между окружностью и прямой, можно найти точку касания и, соответственно, уравнение искомой касательной.
В данной статье мы рассмотрим подробные примеры и шаги по построению касательной к окружности через заданную точку с использованием метода тангенсов. Мы также рассмотрим и другие методы построения касательных, такие как метод секущей и метод приближений. Знание этих методов поможет вам легче справиться с задачами, которые связаны с окружностями и касательными.
Методы построения касательной к окружности через точку
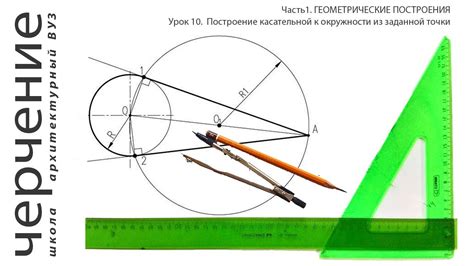
Один из самых простых методов - это использование геометрической конструкции. Для построения касательной к окружности через заданную точку A необходимо провести прямую линию, которая проходит через центр окружности O и точку A. Затем, используя циркуль и линейку, проводятся перпендикуляры к этой прямой находящиеся в точках O и A. Пересечение этих перпендикуляров будет являться точкой касания касательной с окружностью.
Второй метод - это использование алгебраического подхода. Если заданы координаты центра окружности O(x0, y0) и точки A(x1, y1), то уравнение касательной к окружности в точке A имеет вид:
y - y1 = k(x - x1)
где k - это тангенс угла наклона прямой, исходящей из точки A и проходящей через центр окружности O. Зная координаты центра и радиус окружности, можно подставить их в уравнение касательной и решить его относительно переменной x или y.
Третий метод - использование векторного подхода. Если заданы радиус вектор центра окружности O(a, b) и радиус вектор точки A(c, d), то векторное уравнение касательной к окружности в точке A имеет вид:
(a - c)(x - c) + (b - d)(y - d) = 0
где (x, y) - координаты точки на касательной. Это уравнение описывает все точки лежащие на касательной к окружности через заданную точку.
Выбор метода построения касательной к окружности через точку зависит от исходных данных и условий задачи. Каждый из этих методов имеет свои преимущества и может быть более удобным в конкретной ситуации.
Метод 1: Использование радиуса и центра окружности
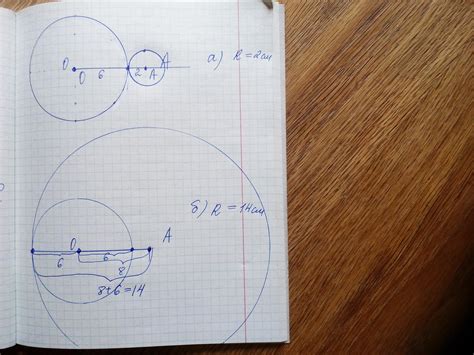
Первый метод построения касательной к окружности через заданную точку основывается на использовании радиуса и центра окружности. Необходимо помнить, что для построения касательной к окружности требуется, чтобы эта точка находилась вне окружности.
Для начала необходимо извлечь радиус окружности и определить её центр. Затем можно приступить к построению касательной. Возможны два варианта:
- Построение вертикальной касательной. Для этого достаточно провести вертикальную линию через центр окружности и заданную точку.
- Построение наклонной касательной. В этом случае необходимо определить угол, который образуется между радиусом окружности и линией, соединяющей центр окружности с заданной точкой. Затем провести линию, которая делает этот угол. Касательная будет пересекать окружность в заданной точке.
Важно отметить, что при построении касательной к окружности через точку необходимо быть аккуратным и точным. Разработчики советуют использовать специализированные геометрические инструменты, такие как циркуль и линейку, для достижения наилучшего качества построения.
Метод 2: Использование заготовленной касательной
Если нам необходимо построить касательную к окружности через заданную точку, мы можем использовать метод, основанный на предварительном построении заготовленной касательной.
Чтобы воспользоваться этим методом, нам понадобится исходная окружность и точка, через которую нужно провести касательную.
Шаги построения:
- Найдите середину отрезка, соединяющего центр окружности и заданную точку. Это можно сделать с помощью построения перпендикуляра, проведенного через середину.
- Проведите прямую через полученную середину и центр окружности. Это будет заготовленная касательная.
- Проверьте, пересекает ли заготовленная касательная окружность в исходной точке.
Теперь у вас есть касательная, проходящая через исходную точку окружности.
Применение этого метода позволяет построить касательную к окружности через заданную точку без использования сложных вычислений или дополнительных построений.
Однако, следует помнить, что при использовании этого метода есть вероятность, что касательная может пересекать окружность в другом месте, кроме заданной точки. Поэтому рекомендуется дополнительно проверять результаты построения.
Метод 3: Использование теоремы о касательной

Еще один способ построения касательной к окружности через заданную точку заключается в использовании теоремы о касательной. Этот метод основан на следующем утверждении:
Теорема о касательной: Прямая, проведенная через точку окружности и перпендикулярная радиусу, является касательной к окружности.
Следуя этой теореме, мы можем построить касательную через заданную точку на окружности следующим образом:
- Определить центр окружности.
- Провести радиус из центра окружности к заданной точке на окружности.
- Построить перпендикулярную данному радиусу прямую через заданную точку.
- Эта прямая будет касательной к окружности в заданной точке.
Используя данный метод, можно эффективно построить касательную к окружности через заданную точку. Этот метод основан на фундаментальной теореме о касательной, что делает его надежным и точным способом.
Примеры практического применения

Еще одним примером применения этого метода является построение оптимального пути для робота. Для этого роботу необходимо выбрать кратчайший путь к заданной точке, учитывая препятствия на его пути. После построения касательной к окружности в текущей позиции робота и пути можно определить оптимальный угол поворота и направление движения, чтобы обойти препятствия и достичь целевой точки.
Еще одним примером применения этого метода может быть определение радиуса кривизны дороги. Допустим, мы хотим узнать, какая часть дороги имеет самый маленький радиус кривизны. Построив касательные к окружностям в разных точках дороги, мы можем определить участки с наименьшим радиусом и принять соответствующие меры для обеспечения безопасности движения на этих участках.